Physics I Quiz 0918
Document everything you do.
An automobile starts from rest and attains a velocity of 20 m/s in the first 10 sec, is moving at 25 m/s at t = 20 sec after starting and at 28 m/s at t = 30 sec after starting. Approximately how far does the automobile move during each of the three 10-second intervals? Do you think your estimate is an overestimate or an underestimate?
What is the average acceleration of the automobile during each of the three 10-sec intervals?
Estimate the instantaneous acceleration at t = 0, t = 10 s, t = 20 s and t = 30 s.
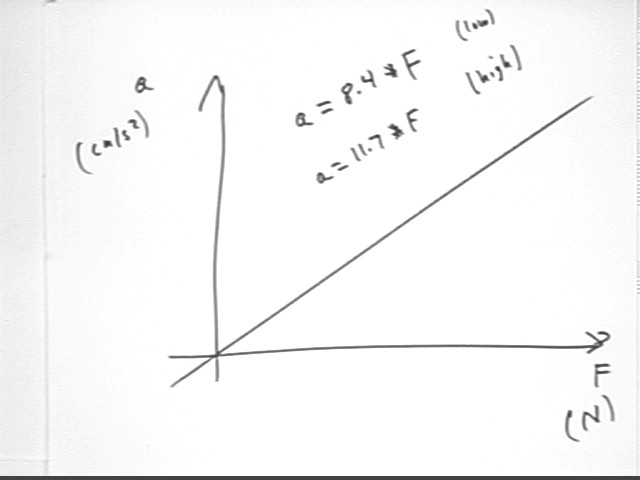
Analysis of results from the experiment performed in the last class (accelerating a chair using stretched rubberbands) tells us that for a in cm/s^2 and F in Newtons we have a = 10 F, approx. The range was a = 8.4 cm/s^2 / Newton * F to a = 11.7 cm/s^2 / Newton * F, neglecting the vertical axis intercepts.
A mean proportionality appears to be a = 10 cm/s^2 / Newton * F.
If a is in m/s^2 then the numbers of the vertical axis are 1/100 as great and we have a = .1 m/s^2 / Newton * F. (More formally 10 cm/s^2 / Newton = (10 cm/s^2 * 1 m / 100 cm ) / Newton = .1 m/s^2 / Newton).
Newton's Second Law tells us that F = m a.




Given that a = .1 m/s^2 / Newton * F what does this tell us about the mass of the object?
Since F = m a implies that m = F / a, we can solve the equation a = .1 m/s^2 / Newton * F for F / a and thereby determine m. We get F / a = 1 / (.1 m/s^2 / Newton) = 10 Newtons / (m/s^2).
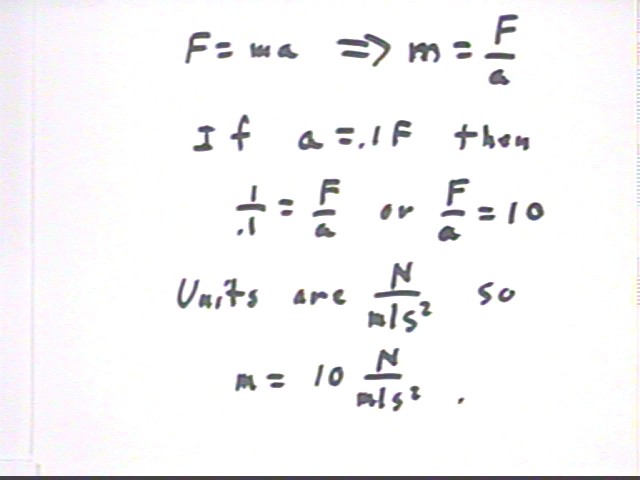
We express all quantities in Physics in terms of the undefined quantities time, mass, length and charge. Charge is not relevant at this point in the course. Standard MKS units of time, mass and length are sec, kg and meter.
The Newton is in fact expressed in terms of these quantities, as indicated below. The Newton is defined, in terms of Newton's Second Law, as a kg m/s^2, the net force required to accelerate 1 kg at 1 m/s^2.
The predicted chair mass F / a = 10 N / (m/s^2) can be simplified to give us the mass in kg.
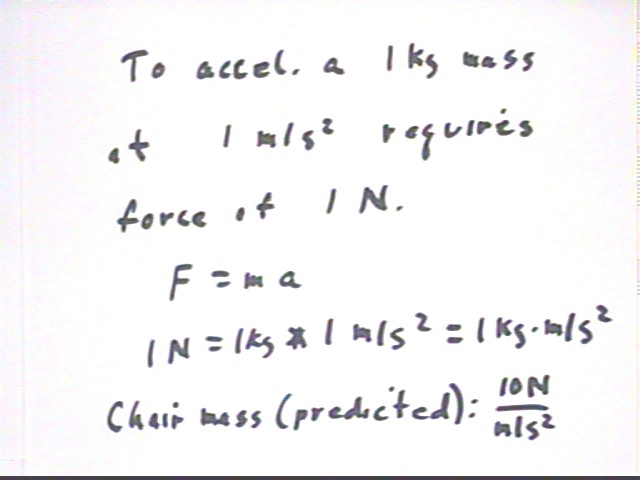
The chair mass predicted by the experiment is therefore 10 kg, with an uncertainty of about +- 1 kg (recall the spread of slopes observed on the graphs created by different groups). Measurement with a spring balance indicates a mass of 9.5 kg, well within the apparent experimental uncertainty.

Quiz Problem from 0916:
The given information, and the assumption that the downward direction is positive, gives us values for v0, a and `ds. From this information we must use either the third or fourth equation of motion. The third would lead to an equation which is quadratic in `dt so we avoid it and use the fourth equation to find vf:
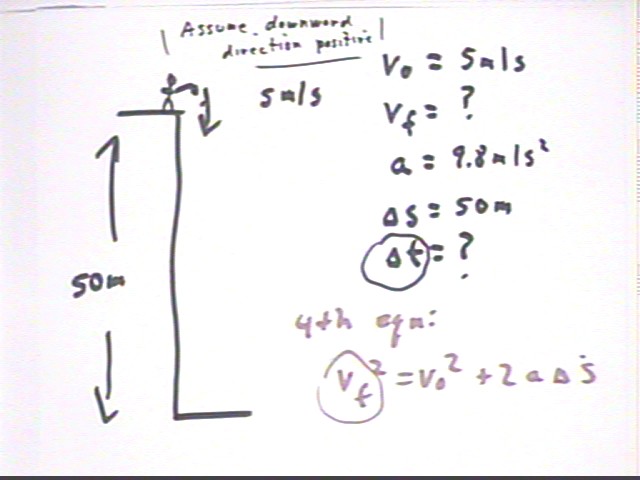
We obtain vf = +- 31.7 m/s, and since downward is the positive direction our choice of the positive value is clear.

We can now find vAve from v0 and vf and from these quantities we use the definition of average velocity and `ds to find `dt. We get `dt = 2.7 sec, approx.
A similar solution for v = 0 would yield `dt = 3.2 sec, approx. So the object which is thrown downward at 5 m/s reaches the ground about .5 sec ahead of an object dropped from rest.

If the object is initially thrown upward at 5 m/s we obtain the same result for magnitude of vf. Note that we chose the upward direction as positive in this example (choice of positive direction doesn't matter except that once it's chosen we need to stick with it).

Because of our choice of pos direction vf in this case it taken to be negative. However just as before we conclude that the velocity after a 50 m fall is 31.7 m/s downward.
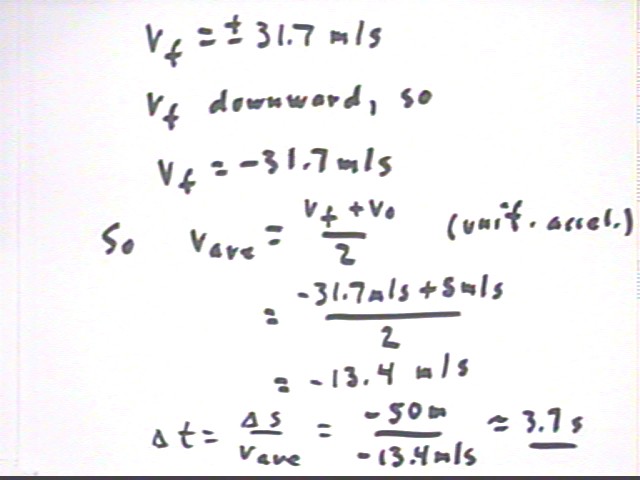
We see that it doesn't matter whether the object is thrown upward or downward at 5 m/s. The final velocity is the same.
We can think of this in terms of energy, which we'll define rigorously in upcoming classes. The ball gains a certain amount of energy as its is vertically displaced 50 meters downward, from start to finish. We give it enough energy to move at 5 m/s and the energy added by the net downward displacement is added to the initial energy, resulting in the final energy regardless of the direction in which the object is initially thrown (throwing the object at 5 m/s downward, upward, or even straight ahead or at some angle wouldn't make any difference in the final energy of motion).
Newton's Third Law: An object at rest will remain at rest, and an object in motion will remain in motion with unchanging speed and direction, unless acted on by a nonzero net force.
Newton's Second Law: The acceleration of an object is directly proportional to the net force acting on it.