
Physics I Quiz 0920
Problem Number 1If at clock times
an object has velocities
then during each of the two time intervals, 0- 9 seconds and 9 - 12 seconds, approximately how far does it move and at what average rate does its velocity change?
If in times .5 sec, 2 sec, 9.25 sec and 9.75 sec a ball rolls down a ramp from rest, starting at different positions on the ramp and starting from rest each time, and covers respective distances of .3011746, .8285943, 2.847338 and 3.519988 cm, does the data support the contention that the acceleration of the ball is independent of velocity and position on the ramp?
Problem Number 3Reason out the quantities v0, vf, Dv, vAve, a, Ds and Dt: If an objectís velocity changes at a uniform rate from 11 cm/s to 15 cm/s as it travels 104 cm, then what is the average acceleration of the object?
Using the equations which govern uniformly accelerated motion determine vf, v0, a, Ds and Dt for an object which accelerates through a distance of 104 cm, starting from velocity 11 cm/s and accelerating at .5 cm/s/s.
Problem Number 4There are ten possible combinations of three of the the five variables v0, vf, a, Dt and Ds. These ten combinations are summarized in the table below:
1 v0
vf
a
2
v0
vf
dt
3
v0
vf
ds
4
v0
a
dt
5
v0
a
ds
*
6
v0
dt
ds
7
vf
a
dt
8
vf
a
ds
*
9
vf
dt
ds
10
a
dt
ds
If we know the three variables we can easily solve for the other two, using either direct reasoning or the equations of uniformly accelerated motion (the definitions of average velocity and acceleration, and the two equations derived from these by eliminating Dt and then eliminating vf).
Only two of these situations require equations for their solution; the rest can be solved by direct reasoning using the seven quantities v0, vf, a, Dt, Ds, Dv and vAve. These two situations, numbers 5 and 8 on the table, are indicated by the asterisks in the last column.
We learn more physics by reasoning directly than by using equations. In direct reasoning we think about the meaning of each calculation and visualize each calculation.
When reasoning directly using v0, vf, `dv, vAve, `ds, `dt and a we use two known variables at a time to determine the value of an unknown variable, which then becomes known. Each step should be accompanied by visualization of the meaning of the calculation and by thinking of the meaning of the calculation. A 'flow diagram' is helpful here.
When using equations, we need to find the equation that contains the three known variables.
Do the following:
A projectile leaves the edge of a table and, while traveling horizontally at a constant velocity, falls freely a distance of 62 cm to the floor. It travels a horizontal distance of 19.7 cm during its fall. If its vertical acceleration is 980 cm/s2, how long does it take to fall and what is its horizontal velocity during the fall?
Solutions to the 9/18 quiz:
The quiz was:
An automobile starts from rest and attains a velocity of 20 m/s in the first 10 sec, is moving at 25 m/s at t = 20 sec after starting and at 28 m/s at t = 30 sec after starting. Approximately how far does the automobile move during each of the three 10-second intervals? Do you think your estimate is an overestimate or an underestimate?
What is the average acceleration of the automobile during each of the three 10-sec intervals?
Estimate the instantaneous acceleration at t = 0, t = 10 s, t = 20 s and t = 30 s.
The most common invalid formula observed on the quiz was `ds = `dv * `dt. The error here is subtle and hard to avoid if you rely on memorizing equations because it looks a lot like the correct `ds = vAve * `dt. However if you think of meanings it is clear which is valid and which is invalid, and the error is very easy to detect by simple standard examples. One such example is given below:

The given information is summarized in the table below. On each interval we can easily find initial and final velocity and time interval. Note that we must use time intervals `dt and not clock times t in calculating displacements and accelerations. Note also that we aren't told that acceleration is constant, and our data don't appear to support constant accelerations, so when we approximate average velocity by averaging initial and final velocities we are only getting an approximation, as indicated by the 'wavy' equal signs. Our average accelerations, however, will be accurate; just keep in mind that acceleration in fact changes, probably continuously, and that we are only getting an average acceleration for each interval.



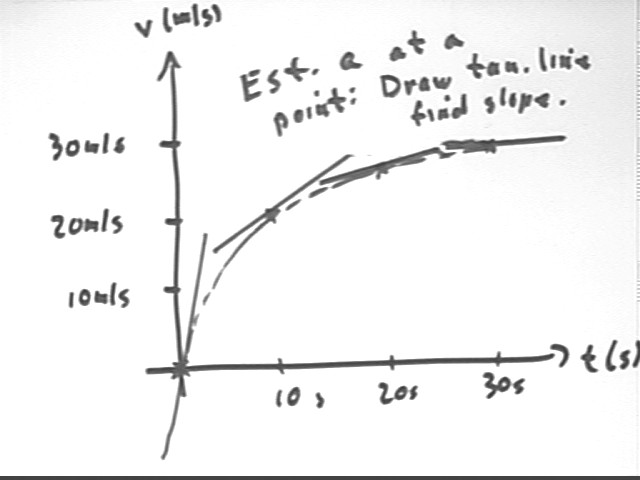
To estimate instantaneous accelerations we need a graph of v vs. t. The graph below indicates the given v vs. t points and provides a smooth curve through those points.
The instantaneous acceleration at an instant is indicated by the slope of a line tangent to the curve at that instant. To estimate the instantaneous accelerations we sketch the best tangent line we can at each point then estimate the coordinates of two points on each line, which will allow us to find approximate change in velocity and change in clock time and hence estimate the slope of each line.
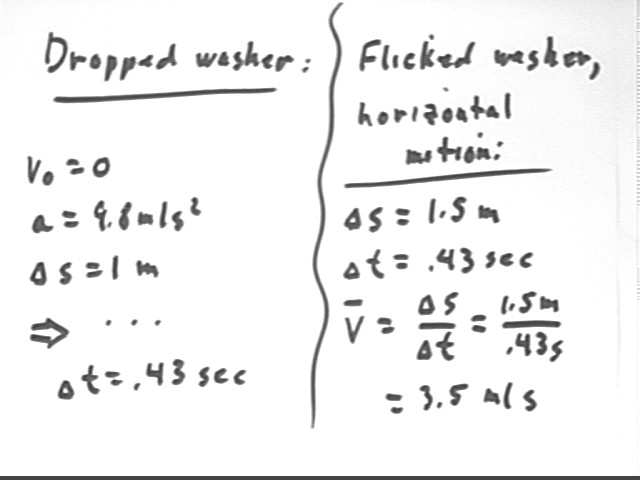
Two washers, one dropped at the same instant and a the same height as the other is flicked off the edge of a table with its velocity wholly in the horizontal direction, hit the floor of the room at the same time. The edge of the table is 1 meter above the floor.
The 'flicked' washer travels 1.5 m before stopping. What is its average horizontal velocity?
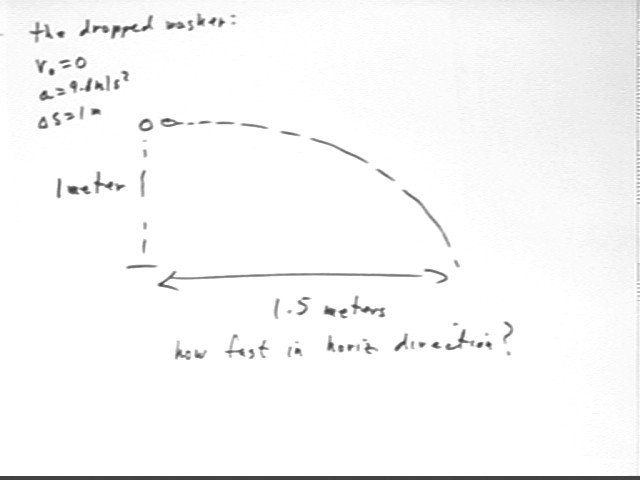
We easily calculate the time required for the dropped washer to reach the floor. The flicked washer required the same time so from its horizontal displacement we easily calculate its average horizontal velocity.
Experiment:
Roll marble down an inclined textbook to a 'constant-velocity' textbook on the edge of a table, from which drops to the floor.
Take data to determine `dsy (vertical drop of the falling marble), `dsx (horizontal range of the falling marble) and 'rise' of the inclined book. Use at least 3 different 'rises'.
Repeat with the 'constant-velocity' textbook on the floor (`dsy will be the thickness of that book).
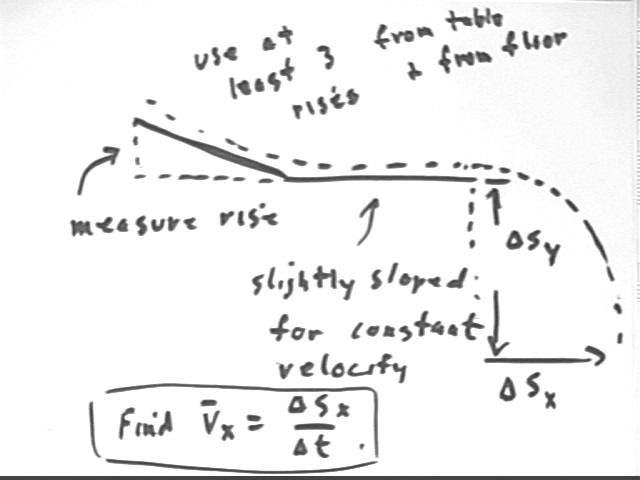
Analysis:
Find average horizontal velocity of the falling ball for each case.
Graph ave. horizontal velocity vs. rise of the inclined book for book on table, and for book on floor.
Calculate the horizontal kinetic energy of the marble for each trial and graph horizontal kinetic energy vs. rise. Marble mass is about 13 grams, KE = .5 m v^2.
Also:
Work out today's 'quiz' and hand in Monday.
Check out other Major Quizzes from Tests link.
Be sure you've mastered the Set 3 problems distributed earlier this week.
- `gGeneral College Physics:
- Read Chapter 4, Sections 1-6 //
- `uUniversity Physics
- Read Chapter 4, Sections 1-5//