Physics Quiz 00923
A straight ramp is inclined at three different slopes. The differences in elevation between one end and the other, for the different slopes, are 2.1, 4.2 and 5.8 cm.
How well do these data confirm our suspicion that the acceleration on the ramp is linearly dependent on the slope?
Unacceptable answer: It confirms it really well. I really mean it!!!!
Sincerity and conviction aside, you have to analyze the data. Find average velocity, final velocity, acceleration.
Ave vel. = `ds / `dt. Init vel is 0. Assume unif accel, so vf = 2 vAve. Then a = `dv / `dt = (vf - v0) / `dt.
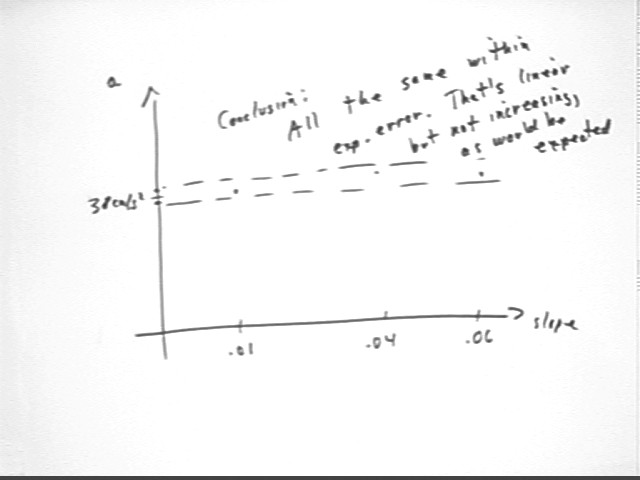
You get three different values of the acceleration, all within 1 cm/s^2 of 38 cm/s^2.
This situation is depicted approximately on the graph in the figure below. The 3 values of the acceleration are confined to a narrow 'band' around 38 cm/s^2. We conclude that withine about a 3% margin around the mean of the three acceleration values, the acceleration is unchanging.
This isn't what we expect, which would be acceleration increasing with slope. However unchanging acceleration implies a horizontal accel vs. slope graph, and a horizontal graph is indeed linear.
Note that slopes are calculated from rise / run, and that the values given on the graph are not accurate. The labeled slopes should be about .04, .08 and .11.

Note the following incorrect equation seen more than once on today's quiz:

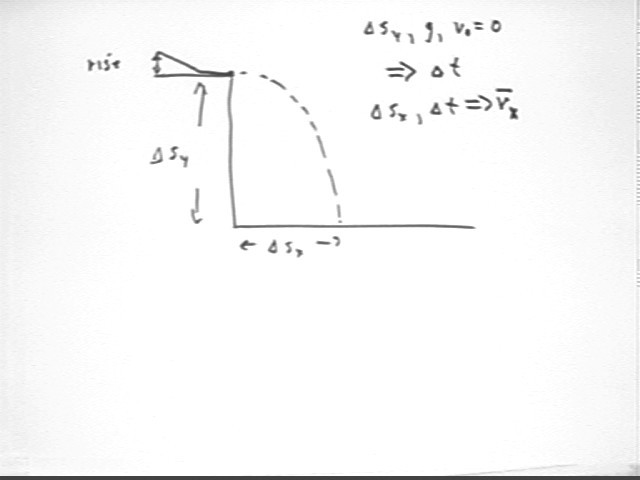
For the experiment from last class, in which rise, `dsy and `dsx were observed (see above figure for general scheme), the following data were observed:
Data (data from book on table with `dsy around 96 cm, then from floor with `dsy around 4 cm):
| rise | `dsy | `dsx |
| 11 | 95.6 | 31.5 |
| 8 | 95.6 | 22.4 |
| 13.2 | 95.6 | 39.6 |
| 7 | 95 | 21.5 |
| 10 | 95 | 33 |
| 13 | 95 | 42 |
| 7 | 96 | 15.5 |
| 10.5 | 96 | 30 |
| 13 | 96 | 37 |
| 12 | 95.5 | 35.5 |
| 17.5 | 95.5 | 43 |
| 8 | 95.5 | 15 |
| rise | `dsy | `dsx |
| 9.3 | 4.2 | 6.1 |
| 11.8 | 4.2 | 8.23 |
| 7 | 5 | 3.5 |
| 10 | 5 | 6 |
| 13 | 5 | 7 |
| 6 | 4 | 3 |
| 7.5 | 4 | 4.5 |
| 10 | 4 | 5.5 |
| 11.5 | 4 | 8 |
| 15.5 | 4 | 11 |
| 8 | 4 | 3 |
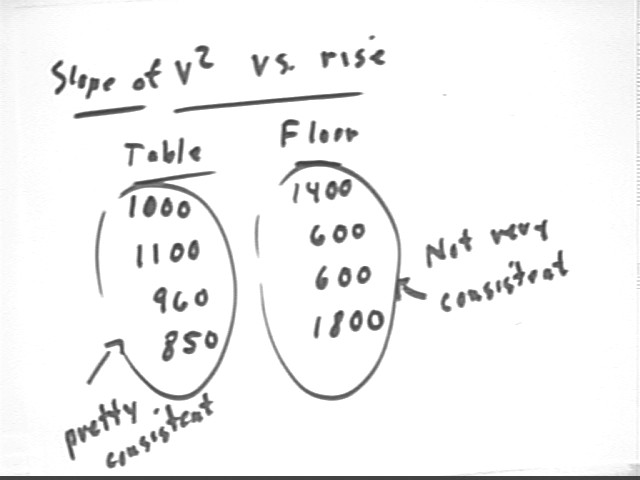
Note that `dsy values for the 'floor trials' differed significantly, perhaps because different books were used.
For all observations, book on table and book on floor:
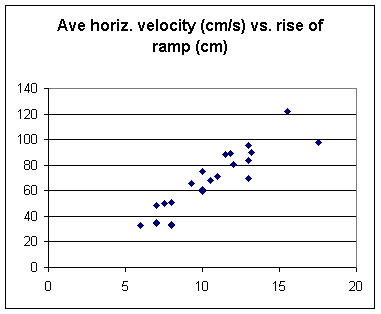
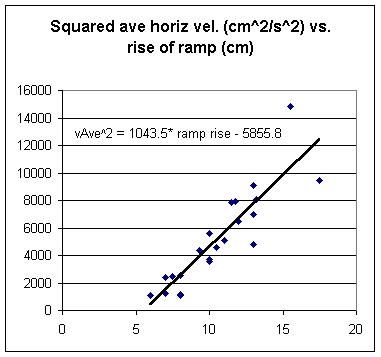
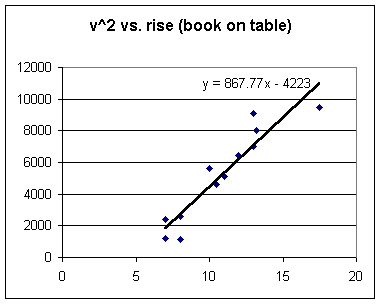
First group v^2 vs. rise, from table then from floor
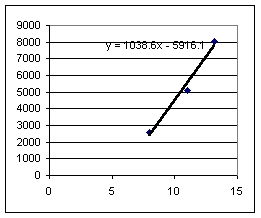
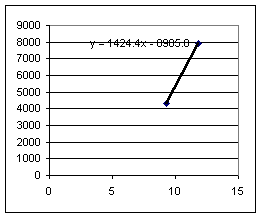
Second group:
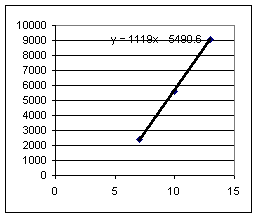
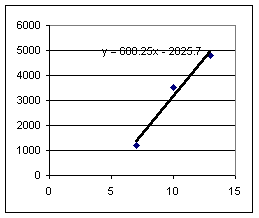
Third group:
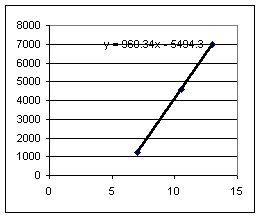
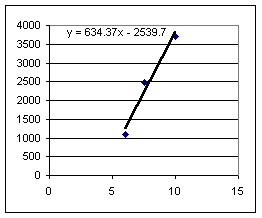
Fourth group:
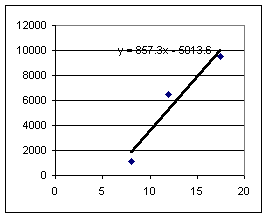
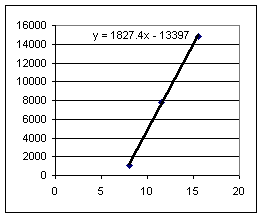
Slopes for the drop with the book on the table are much more consistent than slopes for drop from the book on the floor. This is not surprising, since the fall from the book on the floor is more difficult to 'spot' and since a 1 cm error in horiz range would be about 25% of the horiz distance on floor, but only about 4% of distance on table.
Looking at the combined data for all groups, from the table then from floor, the graph has a greater slope for the 'floor' trials:
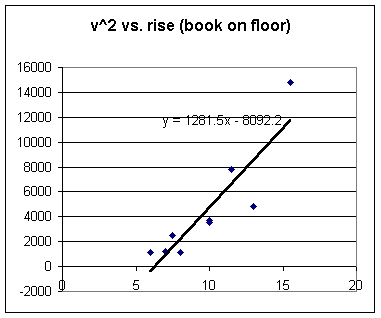
Apparent conclusion, but not with great confidence because of the wide spread in results from floor: Velocities from floor are greater than velocities from table.
We expect same exit velocity (i.e., velocity as the ball rolls off the last book and into freefall) from the same rise, whether on the floor or from the table. So it seems that, since the greater drop apparently has lower ave vel., the ball is losing horizontal velocity as it falls.
However refined experiments will show that this is not the case, that ave horiz vel is same for both cases, excepting to tiny and virtually unobservable changes due to air resistance.
The conclusion of accurate experiments is that horizontal velocity of a projectile, when air resistance is negligible and the range isn't large enough that we need to worry about the curvature of the Earth, is uniform.
If at clock times
an object has velocities
then during each of the two time intervals, 0- 9 seconds and 9 - 12 seconds, approximately how far does it move and at what average rate does its velocity change?
First interval: `dt = 9 sec, `dv = 8 m/s - 9.5 m/s = -1.5 m/s, vAve = (8 m/s + 9.5 m/s) / 2 = 8.75 m/s (approx since unif accel cannot be assumed).
Thus
`ds = vAve * `dt = 8.75 m/s * 9 sec (approx) = 78.75 m,
and
aAve = `dv / `dt = -1.5 m/s / (9 sec) = -.167 m/s^2.
Second interval is done similarly.
Use trapezoids as indicated below. The 'average height' of a trapezoid represents the average of initial and final velocities on the interva (which is an approximation to the actual average velocity which is accurate to the extent that the actual v vs. t behavior is linear)l, the width represents time interval and the 'rise' of the trapezoid represents change in velocity. Thus the area, which is 'ave ht' * width, represents vAve * `dt = `ds, the displacement. And slope = rise / run represents change in vel / change in clock time = ave rate of change of velocity with respect to clock time, or average acceleration.
Note that the approximation of the trapezoidal graph is a linear approximation to the actual behavior. The actual graph would likely be concave downward, so that the linear approximation to average velocity would be an underestimate and the actual displacement would be greater than that predicted by the trapezoidal approximation.
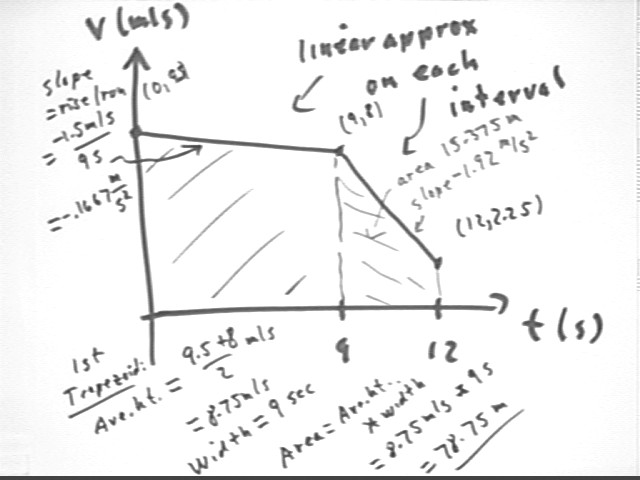
Velocity is rate of change of position with respect to clock time so vAve = `ds / `dt. It follows that `ds = vAve * `dt. Using our linear approximation of velocity on each interval we obtain the results quoted above.
Acceleration is rate of change of velocity with respect to clock time so aAve = `dv / `dt, which we calculate directly as indicated above.
2d interval shows greater negative acceleration, corresponding to coasting up a steeper road
Problem Number 2If in times .5 sec, 2 sec, 9.25 sec and 9.75 sec a ball rolls down a ramp from rest, starting at different positions on the ramp and starting from rest each time, and covers respective distances of .3011746, .8285943, 2.847338 and 3.519988 cm, does the data support the contention that the acceleration of the ball is independent of velocity and position on the ramp?
Same analysis as today's quiz problem but different numbers, probably different conclusions.
Our results for acceleration give us approximately 1.2 cm/s^2,.4 cm/s^2, .3 cm/s^2 and .3 cm/s^2. The last three are reasonably consistent but the first is much different. We could conclude either that the first result was anomalous and that the acceleration is fairly constant, or that the first result was good and that the accelerations were not constant.
Problem Number 3Reason out the quantities v0, vf, Dv, vAve, a, Ds and Dt: If an objectís velocity changes at a uniform rate from 11 cm/s to 15 cm/s as it travels 104 cm, then what is the average acceleration of the object?
We know v0, vf and `ds. Flow diagram can guide our reasoning.
From v0 and vf we get vAve = 13 cm/s and `dv = 4 m/s.
From vAve and `ds we get `dt = 104 cm / (13 cm/s) = 8 s.
Now we have a = `dv / `dt = 4 cm/s / (8 s) = .5 cm/s^2.
Using the equations which govern uniformly accelerated motion determine vf, v0, a, Ds and Dt for an object which accelerates through a distance of 104 cm, starting from velocity 11 cm/s and accelerating at .5 cm/s/s.
We have `ds, v0 and a. In this case we cain't reason out nothin' so we revert to equations.
We find an equation with `ds, v0 and a. We could use the third equation to find `dt or fourth equation to find vf. Much easier to find vf.
We have vf^2 = v0^2 + 2 a `ds so
vf = +- sqrt( v0^2 + 2 a `ds) = +- sqrt( (11 cm/s)^2 + 2 * .5 cm/s^2 * 104 cm) = +- sqrt( 225 cm^2 / s^2) = +- 15 cm/s.
vf = +15 cm/s gives us vAve = (11 cm/s + 15 cm/s) / 2 = 13 cm/s, so that `dt = `ds / vAve = 104 cm / (13 cm/s) = 8 sec.
vf = -15 cm/s gives us vAve = (11 cm/s + (-15 cm/s)) / 2 = -2 cm/s, so that `dt = `ds / vAve = 104 cm / (-2 cm/s) = -52 sec. (example: you started the clock when a cart is rolling downward at 11 cm/s; 52 sec earlier the cart was rolling upward at -15 cm/s).
Problem Number 4There are ten possible combinations of three of the the five variables v0, vf, a, Dt and Ds. These ten combinations are summarized in the table below:
1 v0
vf
a
2
v0
vf
dt
3
v0
vf
ds
4
v0
a
dt
5
v0
a
ds
*
6
v0
dt
ds
7
vf
a
dt
8
vf
a
ds
*
9
vf
dt
ds
10
a
dt
ds
If we know the three variables we can easily solve for the other two, using either direct reasoning or the equations of uniformly accelerated motion (the definitions of average velocity and acceleration, and the two equations derived from these by eliminating Dt and then eliminating vf).
Only two of these situations require equations for their solution; the rest can be solved by direct reasoning using the seven quantities v0, vf, a, Dt, Ds, Dv and vAve. These two situations, numbers 5 and 8 on the table, are indicated by the asterisks in the last column.
We learn more physics by reasoning directly than by using equations. In direct reasoning we think about the meaning of each calculation and visualize each calculation.
When reasoning directly using v0, vf, `dv, vAve, `ds, `dt and a we use two known variables at a time to determine the value of an unknown variable, which then becomes known. Each step should be accompanied by visualization of the meaning of the calculation and by thinking of the meaning of the calculation. A 'flow diagram' is helpful here.
When using equations, we need to find the equation that contains the three known variables.
Do the following:
Given a, `dt, `ds as in situation #10 we can use a and `dt to get `dv, and we can use `ds and `dt to get vAve.
Since vAve is halfway between v0 and vf, which differ by `dv, we know that v0 is vAve - .5 `dv and vf is vAve + .5 `dv (assuming positive `dv; if `dv is negative then v0 will be vAve + .5 `dv , etc. ).
Using equations we can solve the third equation `ds = v0 `dt * .5 a `dt^2 for v0, obtaining v0 = (`ds - .5 a `dt^2) / `dt. We could then use the second equation to find vf = v0 * a `dt.
Direct reasoning doesn't work here.
Given vf, a and `dt we can solve the 4th equation for v0:
vf^2 = v0^2 + 2 a `ds yields
v0 = +-sqrt(vf^2 - 2 a `ds).
Then the second equation vf = v0 + a `dt easily gives us `dt = (vf - v0) / a.
Problem Number 5A projectile leaves the edge of a table and, while traveling horizontally at a constant velocity, falls freely a distance of 62 cm to the floor. It travels a horizontal distance of 19.7 cm during its fall. If its vertical acceleration is 980 cm/s2, how long does it take to fall and what is its horizontal velocity during the fall?
We separate vertical and horizontal motions. Vertical motion has accel = accel of gravity, horiz motion has constant horiz velocity.
Vertical Motion:
v0 = 0, a = 980 cm/s^2, `ds = 62 cm.
We get vf = +-sqrt(v0^2 + 2 a `ds) = ... = 340 cm/s approx..
Thus vAve = (0 + 340 cm/s) / 2 = 170 cm/s and `dt = `ds / vAve = 62 cm / (170 cm/s) = .36 sec.