Physics I Quiz 0927
University and General Physics Students Only:
What average net force does it take to stop a 1500 kg car initially moving at 10 m/s in a distance of 1 meter as its hood crumbles on contact with a concrete wall?
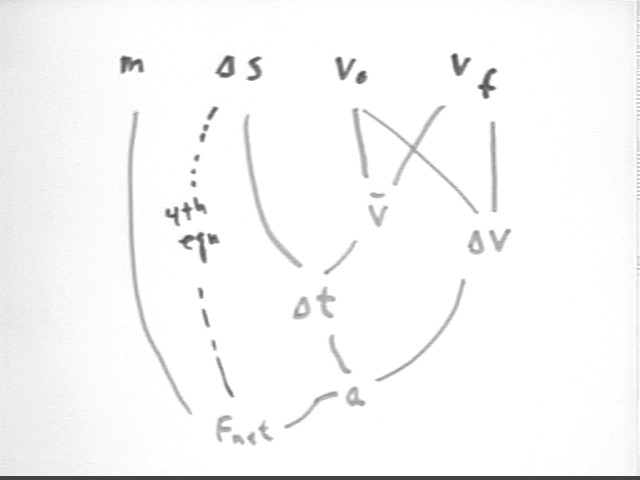
We know `ds, vf (vf = 0), and v0 as well as mass m.
From `ds, vf and v0 we can find acceleration a, which we can then combine with mass to find the average net force.

The detailed calculations are as follows:
From v0 = 10 m/s and vf = 0 m/s we get vAve = 5 m/s.
From `ds = 1 m and vAve = 5 m/s we get `dt = .2 sec.
From v0 = 10 m/s and vf = 0 m/s we get `dv = vf - v0 = 0 m/s - 10 m/s = -10 m/s.
From `dv = -10 m/s and `dt = .2 s we get aAve = `dv / `dt = -10 m/s / (.2 s) = -50 m/s^2.
From m = 1500 kg and aAve = -50 m/s^2 we get FnetAve = 1500 kg * -50 m/s^2 = -75,000 Newtons.
How much work is done by the net force on the car in the process?
`dWnet = Fnet * `ds = -75,000 N * 1 m = -75,000 N m = -75,000 Joules.
What is the effect of a -75,000 Joule net work on an object?
Net work `dWnet = -75,000 Joules decreases the KE of the object by 75,000 Joules.
Note that init KE of the car is .5 * 1500 kg * (10 m/s)^2 = 75,000 Joules, and final KE is 0 so `dKE = -75,000 J.
Note also that the net work done on an object can be negative only if the force acting on it is in the direction opposite to the displacement of the object.
What force is exerted BY the car and how much work is done by this force?
The force exerted BY the car is equal and opposite to the force exerted ON the car. So +75000 Joules is exerted BY the car against the barrier as it moves 1 meter (more precisely, as its center of mass moves one meter). `dWby done BY the car is therefore 75000 N * 1 m = + 75,000 Joules, while the work done ON the car is the equal and opposite quantity -75,000 J.
If `dWnet is work done BY the net force exerted by the car then how are `dWnet and `dKE related?
Several ways to say it. They are equal and opposite, or `dWnet = - `dKE. Or the Work-Energy Theorem:
What is the average force exerted on the 70-kg driver?
Fave = m * a = 70 kg * -50 m/s^2 = 3500 Newtons.
All students:
As you uniformly accelerate a rolling chair with mass 12 kg through a displacement of 4 meters in 2 seconds, what is the acceleration and what is the tension in the rubber band system with which you are accelerating it?
We are given mass m, displacement `ds, time interval `dt and intial velocity v0. The flow diagram below illustrates this situation.
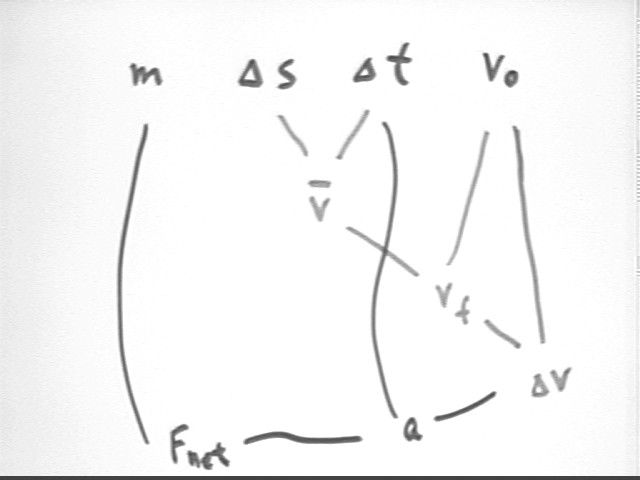
From `ds and `dt we get vAve = 4 m / (2 s) = 2 m/s.
Since v0 = 0 and accel is unif we get vf = 2 * v0 = 4 m /s.
From vf and v0 we get `dv = vf - v0 = 4 m/s - 0 m/s = 4 m/s.
From `dv and `dt we get a = `dv / `dt = 4 m/s / (2 sec) = 2 m/s^2.
From a and m we get Fnet = 2 m/s^2 * 12 kg = 24 kg m/s^2 = 24 Newtons.
This net force is the direct result of the tension in the rubber band.
How much work do you do in the process?
`dWnet = Fnet * `ds = 24 N * 4 meters = 96 Newton meters = 96 Joules.
What is the final kinetic energy of the chair?
KEf = .5 m vf^2 = .5 * 12 kg * (4 m/s)^2 = 96 kg m^2 / s^2 = 96 Joules.
Since KE0 = 0 we see that change in KE = work by net force.
If an object of mass 8.1 Kg and initially at rest is pushed by a net force of 52.65 Newtons for 5.1 seconds, what are its acceleration, its final velocity, its average velocity, and the distance it travels?
We know m, Fnet and `dt; also v0 = 0. Given m, Fnet, `dt and v0 we can draw the conclusions illustrated in the diagram below:
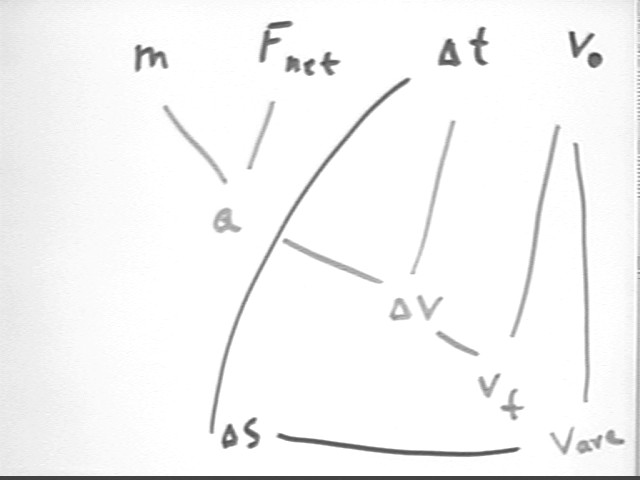
We find
a = Fnet / m, then put that together with `dt to get
`dv = a * `dt, which we put together with v0 to get
vf = v0 + `dt, which we put with v0 to get
vAve = (vf + v0) / 2, which we put with `dt to get
`ds = vAve * `dt.
We get a = 52.65 N / 8.1 kg = 7 m/s^2 approx.
We then get `dv = 7 m/s^2 * 5 sec = 35 m/s (approx.)
Since v0 = 0 we get vf = v0 + `dv = 35 m/s.
vAve = (35 m/s + 0 ) / 2 = 17.5 m/s so
`ds = 17.5 m/s * 5 sec = 88 meters approx.
How much work is done in the process, and what is the change in the KE of the object?
`dWnet = F net`ds = 56 N * 88 m = 5000 N m = 5000 Joules.
Change in KE is
KEf - KE0 =
.5 m vf^2 - .5 m v0^2 =
.5 * 8 kg * 35 (m/s)^2 - .5 * 8 kg * (0 m/s)^2 =
5000 Joules (approx.)
This confirms that `dKEnet = `dWnet.