Notes from Class 1002

Physics I Quiz 1002

University and General College Physics Students:  

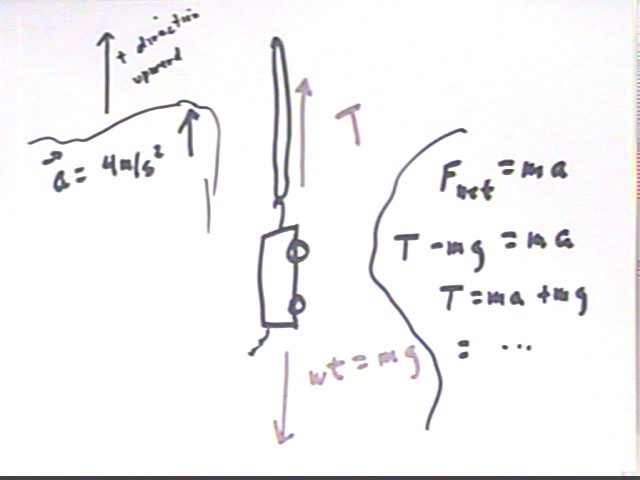
A rubber band has maximum unstretched length 8 cm.  For every additional cm of length it exerts a force of 1 Newton.  A small cart of mass .15 kg is suspended from the rubber band and accelerated upward at 4 m / s^2. 

List the forces acting on the cart and give the direction of each.

A simple demonstration with a rubber band and a mass illustrates how the hanging mass itself stretches the rubberband, creating tension, and how the rubberband stretches even more when the system  is accelerated upward.

We first choose the upward direction as positive, then note that the accleration, which is upward, will also be positive.

If we ignore air resistance we see that the forces acting on the cart are the tension in the rubberband and the weight of the cart.

What is the net force acting on the cart?

As indicated in the figure the net force is Fnet = m a.  In this case Fnet = .15 kg * 4 m/s^2 = .6 Newtons.  This force is positive, therefore upward, in the same direction as the accleration.

How much force is exerted by gravity?

Gravity exerts the force which we call weight, which is equal to the product m g of the mass of the object and the acceleration of gravity.  In this case we have wt = m g = .15 kg * 9.8 m/s^2 = 1.47 Newton.

How much force is therefore exerted by the rubber band?

Fnet = m a and Fnet = T - m g so we have

T - m g = m a and

T = m a + m g = 1.5 kg * 9.8 m/s^2 + 1.5 kg * 4 m/s^2 = 1.47 N + .6 N = 2.07 N.

All students:

If -51 Joules of work are done by a system against the net force acting on it, then by how much does the KE of the system change?

Work-energy Theorem says that `dKE + `dW = 0, where `dKE is the change in the KE of the system and `dW is the work done BY the system.

If `dW = -51 J, as it is here, then `dKE + -51 J = 0 so `dKE = +51 J.

Example:  If I accelerate a mass upward from rest (e.g., the cart in the first problem), I exert a force in the upward direction, and the system exerts an equal and opposite force on my hand.  The force exerted BY the system  is in the direction opposite its displacement so the mass does negative work, thereby increasing its KE. 

In the example of the cart being accelerated upward the force exerted by my hand is not the net force.  The net force includes the gravitational force--i.e., the weight of the cart.  The net force does positive work ON the system  and the system therefore does negative work against the net force--i.e. the work done BY the system against the net force is negative.  Again, note that since the net force is in the direction of motion this increases the KE.

If -91 J of net work is done by a system while  5 J of work are done on the system by nonconservative forces, then by how much do the PE and the KE of the system change?

`dW can be expressed as `dWcons + `dWnoncons, all work regarded as work done BY the system.

`dW = -91 J, `dWnoncons =  -5 J and therefore 

`dWcons = `dW - `dWnoncons = -91 J - (-5 J) = -86 J.

The work done BY the system against a conservative force, which is the negative of the work done ON the system by that force, is the PE change of the system.

`dWcons = `dPE = -86 Joules.

A more detailed form of the work-energy theorem includes the breakdown of `dW into the work done against conservative forces and against nonconservative forces:

`dKE + `dW = 0 so

`dKE  + `dWnoncons + `dWcons = 0 or

`dKE + `dWnoncons + `dPE = 0.

Remember that all `dW's are BY the system.

Gravity acts downward on a falling object and therefore, if the object is falling downward, does positive work on the object.  But how does the object exert force on gravity, thereby doing negative work against gravity?

If the object is falling in Earth's gravitational field, then the object exerts just as much force on Earth as Earth does on the object, but in the opposite direction.  Being less massive than Earth the object's acceleration toward Earth is much greater than Earth's acceleration toward the object (which, since the Earth isn't rigid anyway, is a complicated thing).  So we aren't aware of the effect of the object's force on Earth, which is why this can be  confusing.

Experiment:

Determine the height to which a single folded-up piece of paper can be projected by pulling back a pair of rubberbands 1 cm, 2 cm and 3 cm beyond their maximum unstretched lengths.

Determine the change in the potential energy of the paper.

Determine the average force exerted by the rubberbands, assuming a total 1.5 Newtons of force per cm of pullback, and use this average force and the pullback distance to determine the work done by the rubberbands.

Compare the work done by the rubberbands with the change in the potential energy of the paper as it rises.

Calculate the velocity the paper would have if all the work done by the rubberbands went into its KE.

Calculate the height to which the paper would rise if its velocity when released by the rubberbands was equal to the velocity you just calculated, and compare with the height to which it did rise.

Discuss all energy considerations involved in the process from the start of pullback to the instant the paper reaches its maximum altitude.

Note that the mass of a single sheet of paper is about 3 grams.