Physics I Quiz 1007
University Physics Students (General College Physics and Principles of Physics students may also attempt this problem, which doesn't directly involve any concepts we haven't covered in all classses):
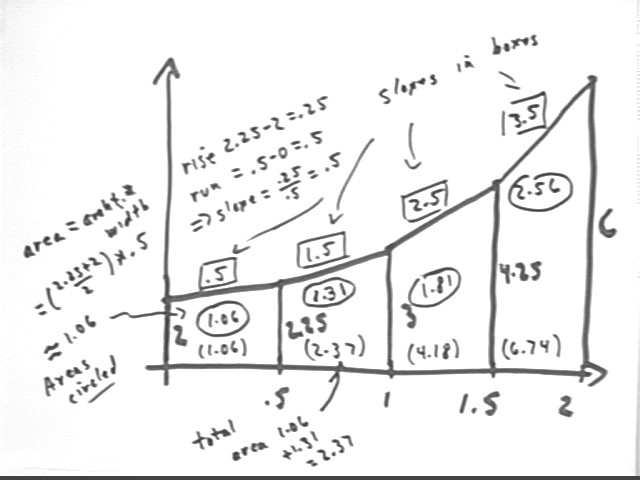
The graph shown below represents the net force F in Newtons vs. position x in meters exerted on a 5-kg object as it is pulled upward. The object is initially at rest at position x = 0. The forces are 2 N, 2.25 N, 3 N. 4.25 N and 6 N at positions 0, .5, 1, 1.5 and 2 meters.
According to the piecewise straight-line approximation of the graph what is the kinetic energy of the object at each of these positions?
The work done on the object by the net force thru a displacement `ds is `dW = Fave * `ds. Since each trapezoid has an average altitude which represents approximate Fave and a width which represents `ds, the area of each trapezoid represents approximate Fave * `ds = `dWbyNet by the net force on that interval. Units will be in Newtons * meters = Joules.
On the first interval we have `dWbyNet = 1.06 Joules. Since the object starts from rest at position x = 0 this will represent its KE at position x = .5 m.
On the second interval we have `dWbyNet = 1.31 J. This will be the change in KE on the second interval, on which it starts with KE of .106 Joules. It therefore ends the second interval with 1.06 J + 1.31 J = 2.37 J.
We see that the area of each trapezoid will be added to the areas of preceding trapezoids to give us the KE at the 'end' of that trapezoid. We get KE 4.18 J at x = 1.5 m and 6.74 J at x = 2 m.

University and General College Physics Students:
Masses of 10 kg and 11 kg are connected by a thread passing over a pulley of negligible mass and friction. The force exerted by gravity on the greater mass tends to pull the system in the clockwise direction, which we will regard as the positive direction, while the force on the lesser mass tends to pull the system in the counterclockwise direction.
What is the net force on the system?
The weights exert forces of 108 N and 98 N, approx., in the clockwise and counterclockwise directions, respectively.
The net force is therefore 10 N in the clockwise direction.
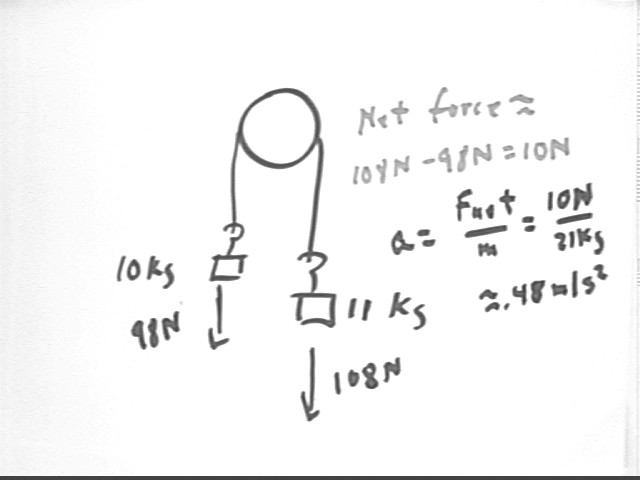
What is the acceleration of the system?
Acceleration is therefore a = Fnet / mass = 10 N / (21 kg) = .48 m/s^2, approx..
If the system starts from rest, what will therefore be its velocity after moving .8 meter? What will be its KE at this point?
Accel is .48 m/s^2, v0 = 0, `ds = .8 meter and vf will be positive so
vf = + sqrt( v0^2 + 2 a `ds ) = ... = .9 m/s, approx.
So KE = .5 m v^2 = .5 * 21 kg * (.9 m/s)^2 = 8 Joules, approx.
By how much will the gravitational potential energy of the greater mass change and by how much will the gravitational potential energy of the lesser mass change?
Change in gravitational PE is equal to work done by the system against the gravitational force. In this case the force exerted against gravity is m g, exerted upward (against the downward force of gravity). If `dy is the displacement of the object, with the upward direction being positive, then it follows that PE change is `dPE = m g * `dy.
Thus as indicated in the figure below the PE change of the 11 kg mass is about -95 J, the PE change of the 10 kg mass is about +87 J so PE change of system is -95 J + 87 J = - 8 J approx..

How does the change in gravitational PE compare with the change in the system's KE?
We see that the changes are equal and opposite (approx. -8 J and approx. 8 J, respectively). This is consistent with conservation of energy:
Conservation of energy tells us that `dW + `dKE + `dPE = 0, where `dW is the work done by the system against nonconservative forces and `dPE is the work done by the system against conservative forces. In this example `dW = 0 (the only force we are considering is gravitational) so we are left with `dKE + `dPE = 0.
Changes are equal and opposite. `dKE + `dPE = 0 in this case where the only forces are gravitational.
Note:
All students:
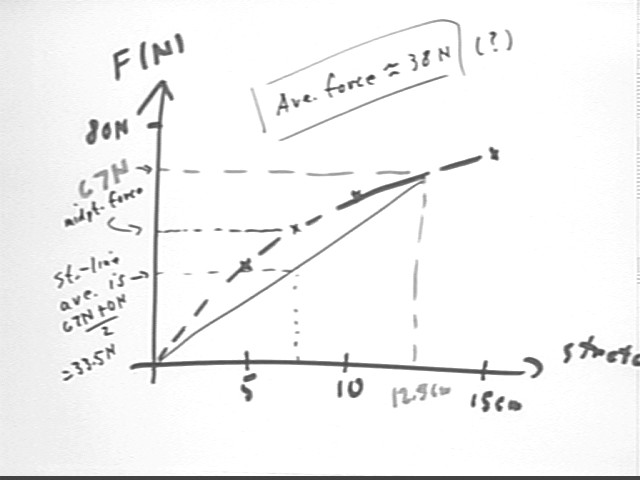
A rubber band exerts forces of 34.70401 Newtons, 57.16382 Newtons and 76.54326 Newtons when stretched along a horizontal surface by 5 cm, 10 cm and 15 cm.
The graph is shown in the figure below.
From the graph we estimate force 67 N at 12.5 cm stretch. Our first estimate of the average force exerted by the rubber band between the 12.5 cm position and position 0 would be the average of 0 N and 67 N or 33.5 N; the graph is concave down so ave force is a bit higher than this. Let's estimate a 38 N ave. force.
Note, mostly for University Physics but accessible to all:
The situation for the .105 kg mass is depicted below. We see decreasing forces acting over the 12.5 cm displacement from release to the equilibrium point of the rubber band. The force decreases from about 67 N at the initial point to 0 N at the equilibrium point. We use our 38 N estimated ave force to get the work F * `ds done on the system by the rubber band; since the rubber band force and the displacement are in the same direction we see that positive work is done on the system.
The work is therefore
`dWon = 38 N * 12.5 cm = 38 N * .125 m = 4.75 Joules.
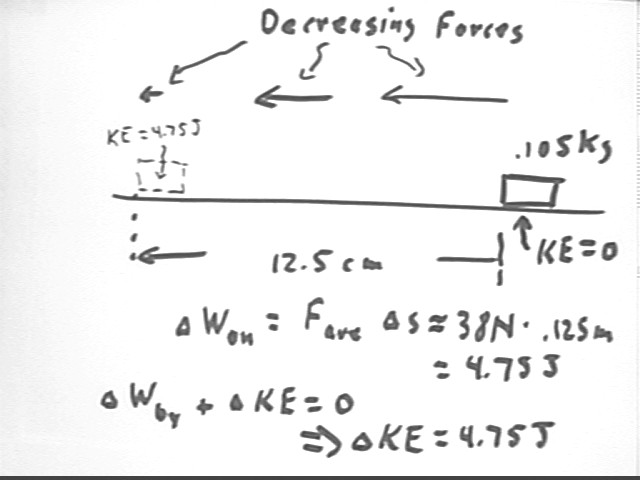
This is the work done on the mass by the rubber band. Since there is no frictional force and since gravity acts perpendicular to the direction of motion, this is the work done by the net force on the mass, and we conclude that the work done BY the mass is the negative of this result:
`dWby = -4.75 J.
Since `dKE + `dWby = 0 we have `dKE = +4.75 Joules.
Since the object starts from rest, with KE zero, we see that its KE at the equilibrium position is 4.75 Joules.
Thus we have a mass of .105 kg with KE 4.75 Joules. Its velocity is thus v = +-sqrt(2 * KE / m) = +-sqrt(2 * 4.75 J / (.105 kg) ) = +- sqrt(91 J) = +- 8.5 m/s.
The forces acting on the mass are the weight, directly downward; Fnormal acting perpendicular to the incline and therefore directly upward, and the frictional force f, which acts in the direction opposite to that of motion. While the rubber band is pulling on the system there is also a force in the direction of `ds, but since this force does not act over most of the coasting distance it is not indicated except by the presence of the rubber band.
Since the system is in vertical equilibrium the two vertical forces add up to zero, so the normal force is equal and opposite to the weight. The magnitude of the normal force is thus Fnormal = m g = .105 kg * 9.8 m/s^2 = 1.03 Newtons. The frictional force is .03 * Fnormal:
Frictional force = .03 * normal force = .03 * 1.03 N = .03 N approx.
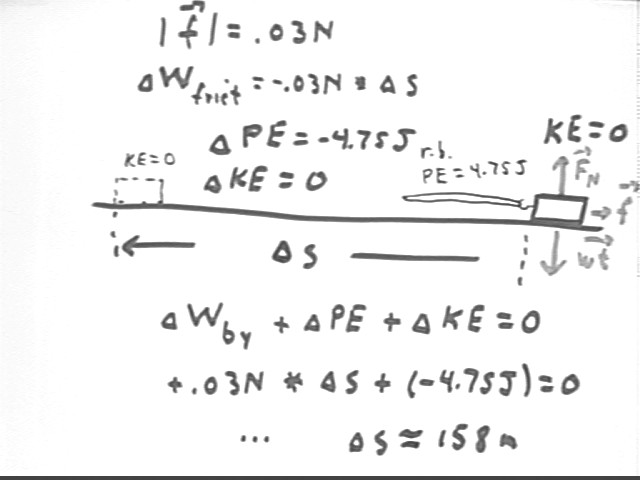
The work done by friction is therefore -.03 N * `ds, where `ds is the displacement of the object across the surface (direction of `ds is assumed positive).
Work of the system against friction is therefore .03 N * `ds.
By energy conservation the -4.75 J of work done by the system against rubber band plus the work .03 N * `ds done by the system against friction is equal and opposite to the KE change of the system:
`dWnet + `dKE = 0.
Work by net force is -4.75 J + .03 N * `ds; system was originally at rest and system came to rest so `dKE = 0.
(-4.75 J + .03 N * `ds) + 0 = 0 and
.03 N * `ds = 4.75 J so
`ds = 4.75 J / (.03 N) = 158.3 meters.
Since `dWnet consists of work done against both conservative and nonconservative forces it can be broken down into work done against the conservative rubber band force, which is `dPE, and the work done against the nonconservative frictional force, which we denote `dWnoncons. Now the -4.75 J of work done against the rubber band force is regarded as potential energy change; its negative value shows that the PE of the rubber band is decreasing (i.e., it holds less and less energy as it snaps back). The work `dWnoncons done by the system against friction is positive, corresponding to the fact that the system exerts a force in its direction of motion to oppose friction. We have
`dWnoncons + `dWcons + `dKE = 0 or
`dWnoncons + `dPE + `dKE = 0 which again gives us
-4.75 J + .03 N * `ds + 0 = 0 and
.03 N * `ds = 4.75 J so
`ds = 4.75 J / (.03 N) = 158.3 meters.