Notes from Class 1009

Physics I Quiz 1009

University Physics Students (General College Physics and Principles of Physics students may also attempt this problem, which doesn't directly involve any concepts we haven't covered in all classses):  

If the net force exerted on an object of mass 12 kg is given by F(x) = - .2 x^3 Newtons / m^3, where x is the position of the object, then what is the work done by the object against the net force as position changes from x = 3 meters to x = 1 meter?  If the object started from rest at the x = 3 m position what is its KE at the 1 meter position?

The force exerted ON the object is -.2 x^3 N/m^3, so the force exerted BY the object against this force is +.2 x^3 N/m^3.  Let `dW be the work done by the object against the force.

For any short interval displacement interval `dx, we have `dW = F * `dx, so that F = dW/dx = W ' , the derivative of W with respect to x.  It follows that W is an antiderivative with respect to x of F.

University and General College Physics Students:  

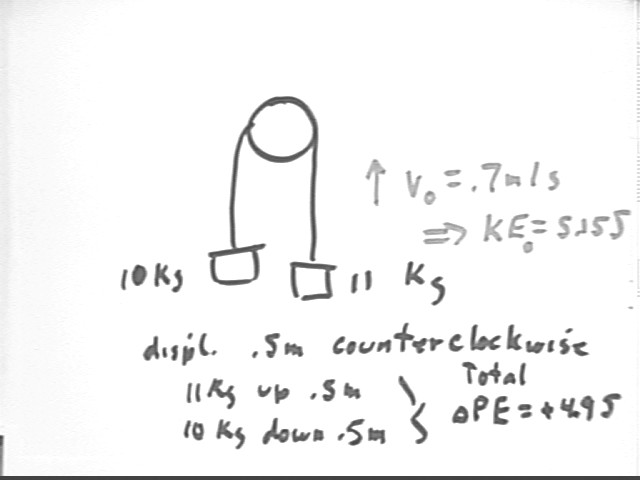
Masses of 10 kg and 11 kg are connected by a thread passing over a pulley of negligible mass and friction.  The force exerted by gravity on the greater mass tends to pull the system in the clockwise direction, which we will regard as the positive direction, while the force on the lesser mass tends to pull the system in the counterclockwise direction.

The system is given an initial velocity of .7 m/s in the counterclockwise direction.  

From given mass and initial velocity we get

KE = .5 m v^2 = .5 * 21 kg * (.7 m/s)^2 = 5.15 Joules.

The 10 kg mass descends and the 11 kg mass ascends.

`dPE of 10 kg mass is 10 kg * 9.8 m/s^2 * (-.5 m) = -49 Joules

`dPE of 11 kg mass is 11 kg * 9.8 m/s^2 * (-.5 m) = +53.9 Joules

`dPE of system is -49 J + 53.9 J = + 4.9 J.

No work is done by nonconservative forces so `dPE + `dKE = 0 so we have

+4.9 J + `dKE = 0 and

`dKE = -4.9 J.

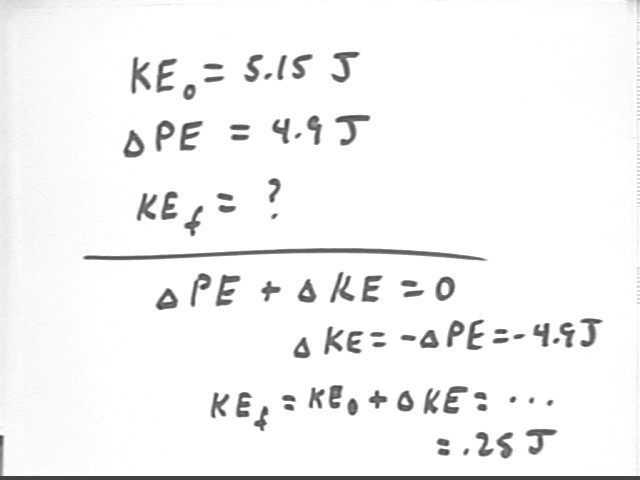
Initial KE was 5.15 J so final KE is KEf = KE0 + `dKE = 5.15 J - 4.9 J = .25 J. 

The system has mass 21 kg and KE is .25 J.

.5 m v^2 = KE so v = sqrt( 2 KE / m).  Thus

v = +-sqrt( 2 * .25 J / (21 kg) ) = +-( .024 (kg m^2 / s^2) / kg) = +-sqrt(.024 m^2/s^2) = +-.15 m/s, approx..

Since the system was initially given a velocity in the counterclockwise direction and since the change in PE has not been sufficient to dissipate all of the initial KE the system will still be moving in the counterclockwise direction.  If this direction is taken as positive then our approximate velocity will be +.15 m/s..

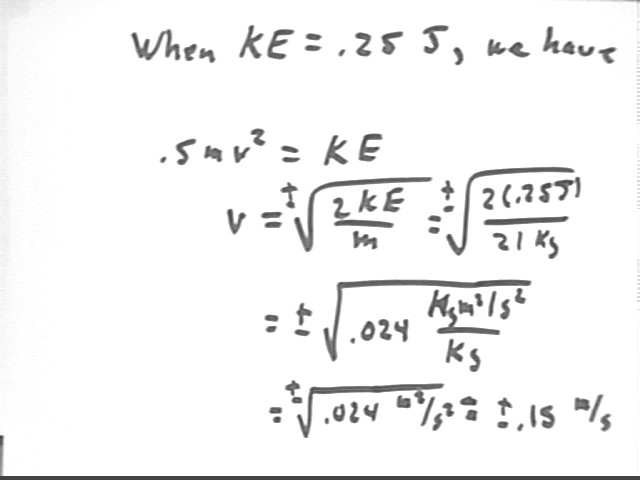
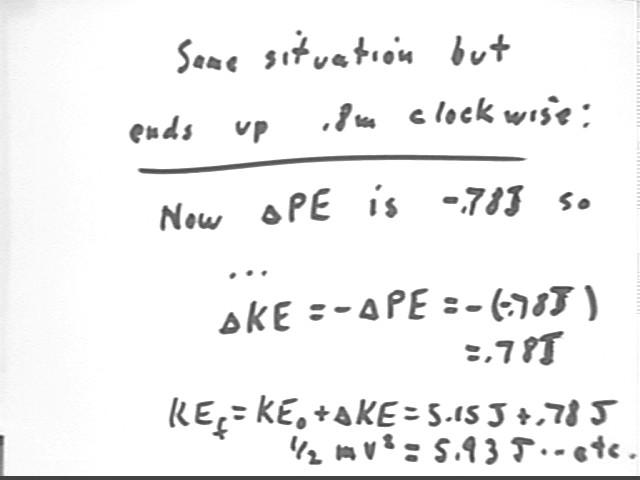
Use the same analysis to determine the KE of the system, again given the .7 m/s counterclockwise initial velocity, when it has undergone a net clockwise displacement of .8 meters.

At net clockwise displacement of .8 meters the 11 kg mass will be lower than originally and the 10 kg mass higher; net change in PE is -.78 Joules, approx..

Init KE is still 5.15 J.

`dPE + `dKE = 0 so

-.78 J + `dKE = 0 and

`dKE =  .78 J.

Thus KEf - KE0 = .78 J and

KEf = .78 J + KE0 = .78 J + 5.15 J = 5.93 J.

So v = +-sqrt( 2 * 5.93 J / (21 kg) ) =+-.61 m/s, approx..

Since the system started out with velocity in the counterclockwise direction and under uniform acceleration ended up moving in the clockwise direction the velocity  at this point must be clockwise.  Retaining the counterclockwise direction as the positive direction we get approximate velocity v = -.61 m/s..

All students:

A mass of 100 kg slides up a frictionless incline until it is 3 meters higher than it was when it started.

How much PE does the system gain during this process?

The displacement parallel to the gravitational force is + 3 m, using the upward direction as positive.

Change in gravitational PE is work done against the gravitational force:  `dPEgrav = 100 kg * 9.8 m/s^2 * 3 m = 2940 Joules.

The tension in the spring varies from 0 N at the equilibrium position to 645 N at .54 m stretch.

An ideal spring is massless, the force is a linear function of displacement from equilibrium, and no energy is dissipated.

The linearity of the force tells us that average force = (0 + 645 N) / 2 so that the work done against spring tension is `dW =   (0 + 645 N) / 2 * .54 m = 174 Joules.

The spring force is conservative (i.e., it can be recovered on release of the spring), so the work done against the spring force constitutes a PE change.  Thus we say that `dPEelastic = 174 Joules.

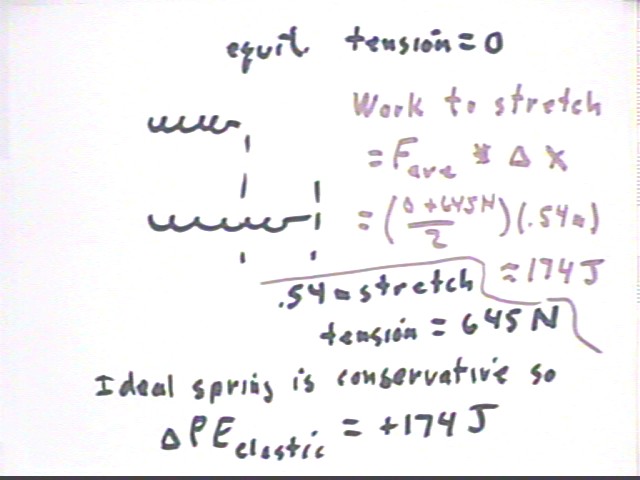
The total PE change of the mass is therefore `dPE = `dPEgrav + `dPEelastic = 2940 J + 174 J = 3110 J, approx..

An 4 kg sledgehammer is raised 2 meters then forcibly brought down on a metal post, which it strikes at 13 m/s.  The post does not move appreciably, being in contact with bedrock.  All work done by nongravitational forces results from burning Cheerios.  How many Joules worth of Cheerios are burnt to raise the sledgehammer?  How many Joules worth of Cheerios are burnt in the process of bringing the sledgehammer down?  After 10 minutes of repeated strikes what sensation will be noticeable to a hand rested on the top of the post?  How would the sensation differ had the process been going on for an hour?

The 4 kg mass has a weight of 4 kg * 9.8 m/s^2 = 39.2 Newtons.  Lifted through a vertical displacement of 2 meters it gains 39.2 N * 2 m = 78 J of KE, approx..  Thus 78 J worth of Cheerios went into lifting the hammer.  Note that the mass of the individual swinging the hammer probably had an upward vertical displacement, requiring even more Cheerios, and that the individual's energy conversion process is only around 15% efficient so that even more Cheerios were actually utilized.

The KE of the sledgehammer when it strikes the post is KE = .5 m v^2 = .5 * 4 kg * (13 m/s)^2 = 338 Joules.  Of this 338 Joules, 78 were supplied by gravity as the gravitational PE decreased to its original value.  The remaining 260 Joules were supplied by the individual (note that some might be supplied by the decreasing PE of the individual, who probably displaces to a somewhat lower position in the process of swinging the hammer; this energy will be restored on the next upswing by the increasing PE of the individual).

Suggested Procedure for analyzing energy:

List all the forces acting on the system, and sketch all forces to scale.

List all the forces exerted by the system, and sketch all forces to scale.

 

List all forces which act on the system parallel to its direction of motion.

If displacement is knows determine the work done by the net force in the direction of motion.

 

List all conservative forces which act on the system parallel to its direction of motion.

Determine the work `dWconservativeON done on the system by conservative forces.

 

List all nonconservative forces which act on the system parallel to its direction of motion.

Determine the work `dWnonconservativeON done on the system by nonconservative forces.

 

Determine the work done BY the system against nonconservative forces.  This is `dPE.

Determine the work done BY the system against conservative forces.  This is `dWnoncons.

 

Apply the principle of conservation of energy.

 

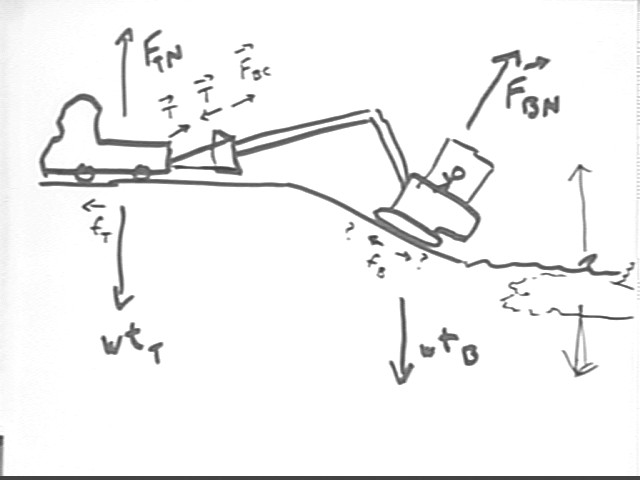
The situation  depicted below summarizes forces on truck, backhoe (and shark).

Normal force F(BN) exerted by the slope on the backhoe is prependicular to the slope.  The weight of the backhoe is directed vertically downward.  The frictional force fBbetween backhoe and slope is directed opposite to the sum of all nonfrictional forces (possibly upward if the bucket pulls upward with enough force to pull the backhoe  up the slope, otherwise downward against the gravitational component parallel to the slope).

The tension T in the chain pulls the bucket forward (i.e., away from the water) and down, and the truck upward and back toward the water.

The frictional force fB between truck and level ground is exerted in the forward direction, opposite to the backward component of the tension acting on the truck.

The normal force F(TN) on the truck is directed upward by the compressed ground, and along with the upward component of the tension will be equal and opposite to the weight of the truck (assuming that the truck is not lifted up by the backhoe).

Note that the upward component of the tension has the effect of reducing the normal force on the truck, which reduces the possible frictional force, tending to defeat the attempt of the backhoe to get away from the shark.  Had the chain been hooked to the bottom of the backhoe the tension might have had a downward component, tending to increase the normal force and enhancing the effort at hand.

(The shark experiences a weight force downward and an equal and opposite buoyant force.)