Notes from Class 1011

Physics I Quiz 1011

Suggested Procedure for analyzing energy:  

Remember that we're trying to make intuitive sense out of the conservation of energy relationship `dKE + `dPE + `dWnoncons = 0, and that `dPE is the work done BY  the system against conservative forces while `dWnoncons is the work done BY the system against nonconservative forces.

1.  List all forces exerted on and by the system:

2.  List all forces exerted on and by the system in the direction parallel to motion and determine work:

3.  Consider conservative forces and find the corresponding work:

3.  Consider nonconservative forces and find the corresponding work:

4.  Find the work done BY the system against conservative and nonconservative forces:

5.  Apply the principle of conservation of energy.

Apply this procedure to the following situations all involving cars on inclines:

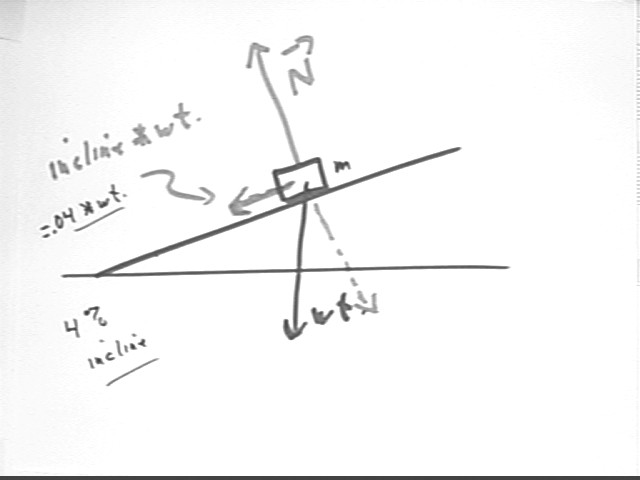
For any object on an incline the weight can be expressed as two components, one in the parallel to the incline and the other perpendicular to it.  These components are combined with forces of friction and air resistance as well as normal force to get net force.

For example for a mass on a 4% incline the weight will resolve into components perpendicular and parallel to the incline, with the parallel component being very close to .04 * weight.

Note for further reference that the accurate value of the parallel component is weight * sin(theta), where theta is the angle of the incline with horizontal.  For small angles sin(theta) is very close to tan(theta), which is the slope.  As the angle gets larger these quantities begin to diverge and the approximation obtained from weight * slope becomes less accurate.

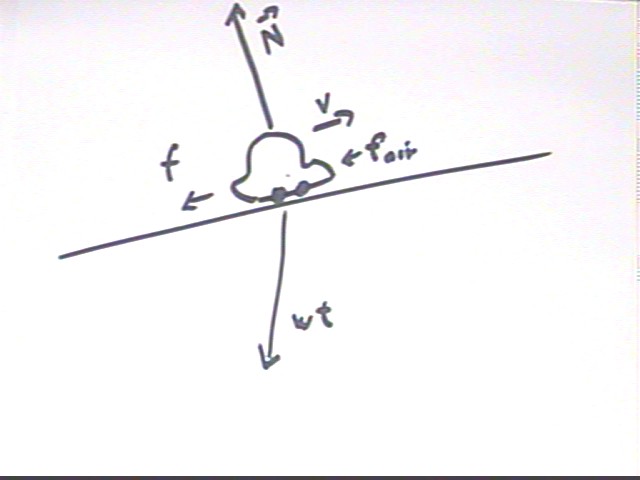
The forces in the direction of motion are the weight component parallel to the incline, friction and air resistance.  Friction and air resistance are in the direction opposite to the velocity v (this assumes that the air is still with respect to the incline; a tailwind, for example, could produce an air resistance in the opposite direction)..

Net force on system is 

Net work on system is net force * displacement.

The only conservative force in this situation is the gravitational force, or weight.  Work ON system by conservative force is product of displacement (up or down incline, depending on situation) and weight component parallel to incline (always down the incline).

Nonconservative forces here include friction and air resistance, which act opposite to the direction of motion and hence do negative work on the system.

Work by system against cons and noncons forces is equal and opposite to work done on system by these forces.

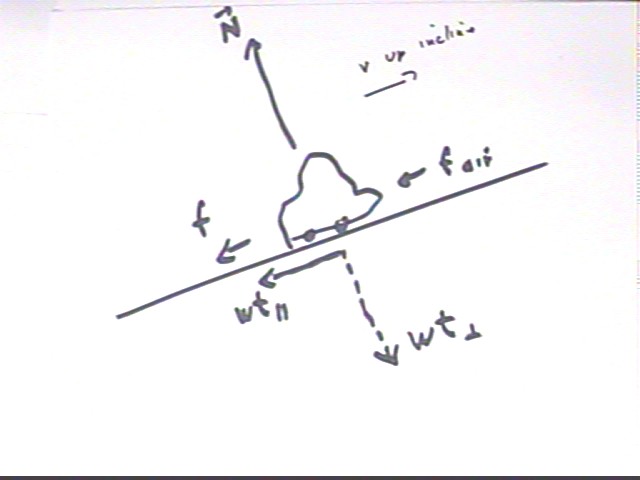
The figure below shows the forces exerted by the car against friction and air resistance (the car must exert forces against these forces so these forces are exerted by the car in the direction of motion), the upward gravitational force the car exerts on the Earth and the force 'down into' the ramp at a perpendicular to the ramp.  This figure shows why the work done BY the system is equal and opposite to the work done ON the system (because the forces exerted BY the system are equal to but in a direction opposite to those exerted ON the system).

The forces exerted on the car can be represented as in the figure below, with the weight replaced by its components parallel to and perpendicular to the direction of motion.  Note that work done against the weight is done against a conservative force, while work done against friction and air resistance are done against nonconservative forces.  

 

 

 

 

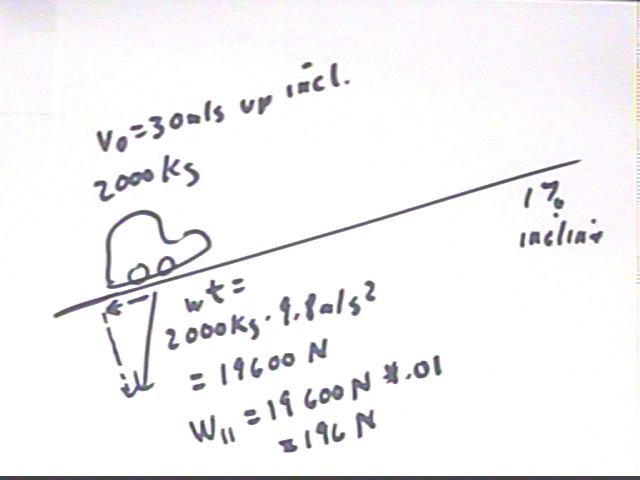
1.  An automobile of mass 2000 kg is moving up a long, constant 1% incline at 30 m/s is put into neutral and coasts 1000 meters.  Assume (somewhat unrealistically) that friction and air resistance are negligible. 

This situation is depicted in the figure below.  We are ultimately going to determine `dKE, `dPE and `dWnoncons within the context of the conservation of energy equation `dKE + `dPE + `dWnoncons = 0.

Note that the car has initial velocity 30 m/s, which gives it initial kinetic energy 

The weight of the car is 19,600 Newtons, which on a 1% incline gives us a weight component of .01 * 19,600 Newtons = 196 Newtons parallel to the incline.

If we ignore friction and air resistance then the only force acting in the direction of motion is the 196 N  gravitational component down the incline.  The work done by this component is -196 N * 1000 m = -196,000 Joules.  Note that this work is done against by a conservative force and will therefore be related to the PE of the system.

Since gravity does -196,000 J of work on the system, the system does +196,000 J of work against gravity.  Thus the PE of the system increases by +196,000 J (change in PE is work done by system against conservative force).

Energy conservation tells us that

We're neglecting nonconservative forces (friction, air resistance) so `dWnon ons = 0 and thus

Since KE0 = 900,000 J we find that after coasting 1000 meters we have KEf = KE0 + `dKE = 900,000 J + (-196,000 J) = 704,000 J.

We could easily find the final velocity of the object from v = +-sqrt( 2 * KE / m).

Again this ignores friction and air resistance, which will be very significant in reality.

Conceptually, when your car coasts up a hill, gravity is pulling in the direction opposite to motion so gravity does negative work on it, which means that the car does positive work against gravity, so its gravitational PE increases.  Since the car is coasting this PE increase is accomplished at the expense of its KE.  If the car doesn't have enough KE it can't coast all the way up the hill.

2.  A 2000 kg automobile coasts freely down a 3% incline, from rest, for a distance of 1000 meters.  Ignore air resistance.  What does energy conservation tell you?

The figure below indicates weight, normal force, the frictional force f and the force fAir of air resistance.  We find that if we ignore friction and air resistance the net force is the 'parallel component' of the weight, which is 588 N down the incline.

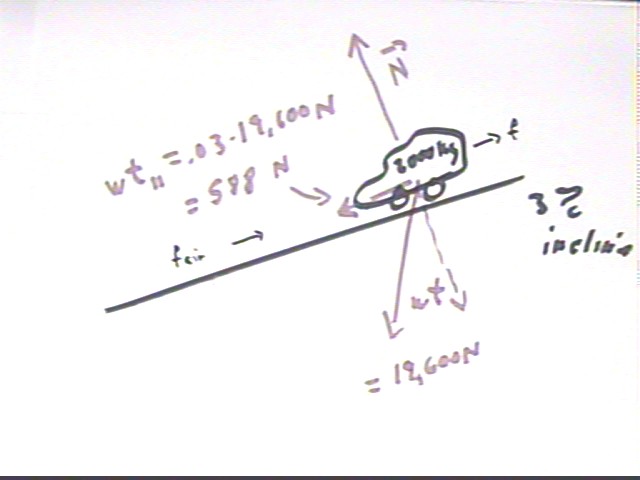
Traveling 1000 m down the incline we see that gravity does 588 N * 1000 m = 588,000 J of work on the system.  This is work done on system by conservative force.  So system does -588,000 J of work against the conservative force--i.e., its potential energy changes by -588,000 J.

If we neglect nonconservative forces we have `dWnoncons = 0 so

`dKE + `dPE + `dWnoncons = 0 gives us

`dKE = - `dPE = - (-588,000 J) = 588,000 J.

Since KE0 = 0 (starting from rest) we have KEf = 588,000 J.

We could easily find v from mass and KE.

3.  A 2000 kg automobile coasts down a 3% incline at a constant 10 m/s for a distance of 1000 meters.  Assume air resistance to be negligible.

`dKE + `dPE + `dWnoncons = 0.

As seen in the preceding problem `dPE = -588,000 J.

`dKE = 0 since velocity is constant.

We conclude that

`dWnoncons = - `dPE = -(-588,000 J) = 588,000 J.

The system does 588,000 J against some unspecified nonconservative force. 

This unspecified nonconservative force could for example be a combination of air resistance and road friction; the 10 m/s velocity could be the velocity at which air resistance becomes just great enough to counter the total of all other forces and make the net force zero, resulting in the 0 acceleration implied by the unchanging velocity.

More imaginative possibilities for the nonconservative force might include a muddy road, rocks in the road, or a flock of suicidal pigeons more or less continuously running into the windshield. 

4.  An automobile drives up a 5% incline, for a distance of 1000 m, at a constant 30 m/s.

The gravitational force component parallel to the incline is .05 * 19,600 N = 980 N, opposite to the upward direction of motion, so gravity does -980 N * 1000 m = -980,000 Joules of work on the system.  The system therefore does +980,000 J of work against gravity, increasing its PE by 980,000 J.  KE does not change so 

`dKE + `dPE + `dWnoncons = 0 gives us

0 + 980,000 J + `dWnoncons = 0 and

`dWnoncons = -980,000 J.

The work done BY the system against nonconservative forces is -980,000 J, so that nonconservative forces do +980,000 J of work ON the system.

The key nonconservative force is the force exerted between the tires of the vehicle and the road.  The point of contact between the wheel and the road is in fact stationary if the wheel is not sliding with respect to the road.  Presumably the engine is driving the drive wheels 'backward', and the resulting frictional force  exerted on the wheels is in the forward direction.