Physics I Quiz 1014
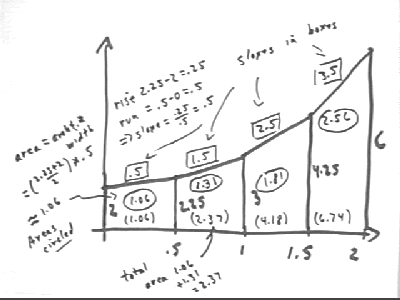
University Physics: What do the slopes and areas of the graph depicted below, showing the net force F, in Newtons, acting on a 10 kg mass vs. clock time t, represent?
The slope of a trapezoid is rise / run, representing change in force / change in clock time, or the time rate, in Newtons / second, at which the force is changing.
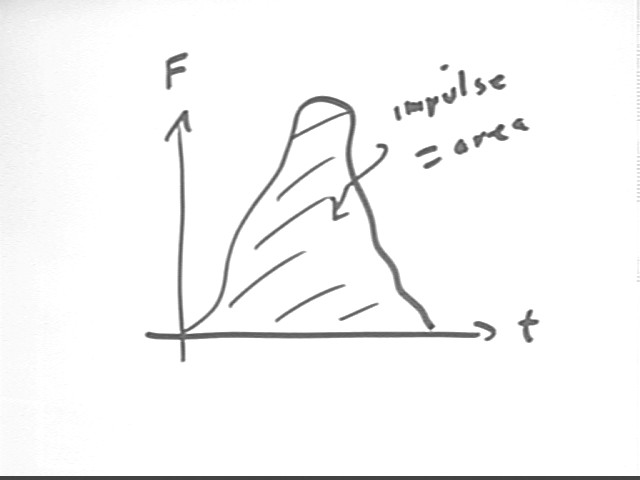
The area of a trapezoid is ave graph altitude * trapezoid width, representing approximate average force * time interval or Fave * `dt, which is the impulse of the force during the time interval represented by the trapezoid.
It follows that the derivative of a force vs. clock time graph is the rate F ' (t) at which force changes with respect to clock time, while the definite integral of a force vs. clock time graph between two given clock times is the impulse of the force between those clock times.

The impulse of a positive force is therefore represented by the area between the t axis and the graph of F vs. t.
All students:
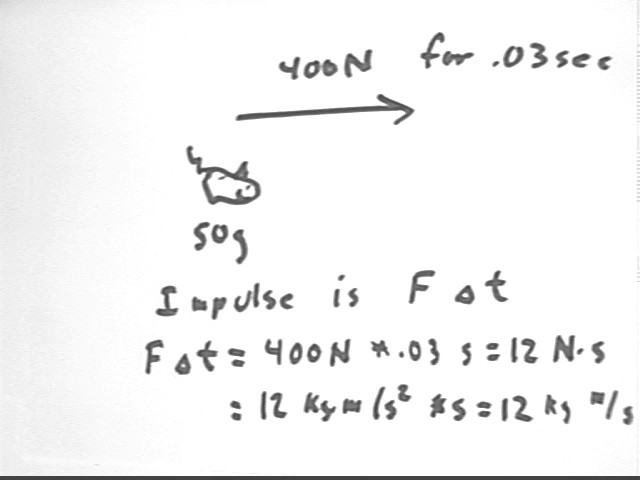
If a net force of 400 Newtons acts for .03 seconds on a 50 gram mass, by how much does the velocity of the mass change?
We could find the result using Newton's Second Law and the ideas of uniformly accelerated motion (accel would be 400 N / (.05 kg) = 8000 m/s^2 so in .03 seconds velocity would change by 8000 m/s^2 * .03 s = 240 m/s). However we choose to apply the impulse-momentum theorem:
F `dt = `d(m v) or for constant mass m
F `dt = m `dv. We obtain
400 N * .03 s = .05 kg * `dv or
12 N * s = .05 kg * `dv or
12 kg m/s^2 * s = .05 kg * `dv or
12 kg m/s = .05 kg * `dv so that
`dv = 12 kg m/s / (.05 kg) = 240 m/s.

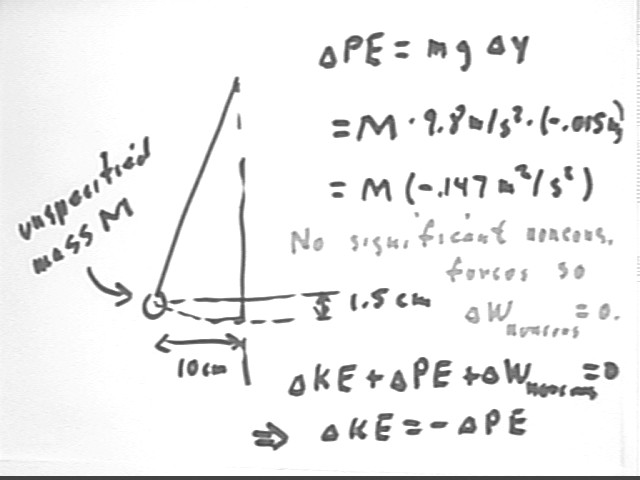
A pendulum of a certain length is pulled back 10 cm, which raises the pendulum 1.5 cm. The pendulum is released. Assuming no energy loss to nonconservative forces, what is its velocity at the instant it reaches its equilibrium position? (Note: It's unnecessary to assign a mass to the pendulum; the mass can simply be represented as M. However if you feel that you really need to specify the mass you may use any constant mass you wish).
The PE of the pendulum decreases by M * g * `dy = M * 9.8 m/s^2 * (-.015 m) = M * (-.147 m^2 / s^2).
Presumably the pendulum is released from rest so its initial KE is 0.
If no nongravitational forces act on the pendulum, which in typical applications is pretty much the case, we have `dWnoncons = 0 so that
`dPE + `dKE = 0 and
`dKE = - `dPE so
KEf - KE0 = `-dPE and since KE0 = 0
.5 M vf^2 = M ( .147 m^2 / s^2). Solving for vf we have
vf = +- [ M ( .147 m^2 / s^2) / (.5 M) ] = +-sqrt(.294 m^2 / s^2) = +-.54 m/s, approx.

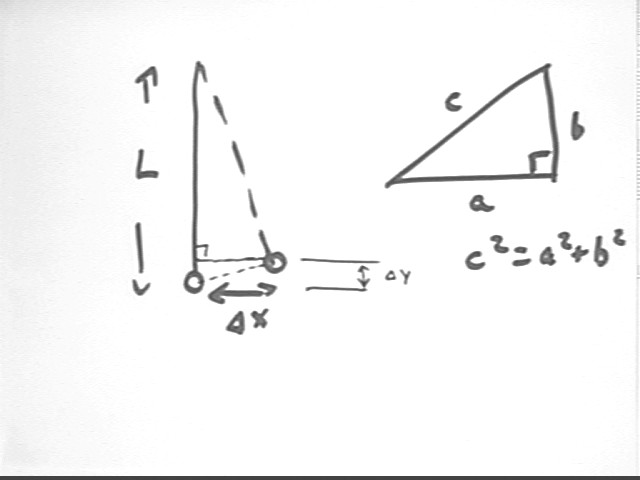
Note for future reference that it is possible to construct a right triangle with L as the hypotenuse and horizontal displacement `dx as one leg, as indicated below. The height `dy to which the pendulum is raised is the difference between the length of the vertical side of this triangle, which is easily found using the Pythagorean Theorem, and the length of the pendulum.
We now understand most of the quantities in terms of which we do physics.
We started with the basic undefined quantities, which include mass, length and time (as well as Coulombs, with which we haven't yet dealt).
Then using the idea of rate we defined velocity and acceleration.
From acceleration and mass we determine net force, according to Newton's Second Law.
From force and displacement we define work/energy. Since `dKE = work done by the net force acting ON a system by the net force acting on the system we see that `dKE + `dWnet = 0, where `dWnet is the work done BY the system AGAINST the net force acting on it. This is the work-energy theorem. Breaking `dWnet into `dPE, the work done by the system against conservative force, and `dWnoncons, the work done by the system against nonconservative forces, we express this as `dKE + `dPE + `dWnoncons = 0.
From force and time interval we get impulse F `dt, which is equal to `d (mv), the change in momentum. When m is constant, `d(mv) = m * `dv.

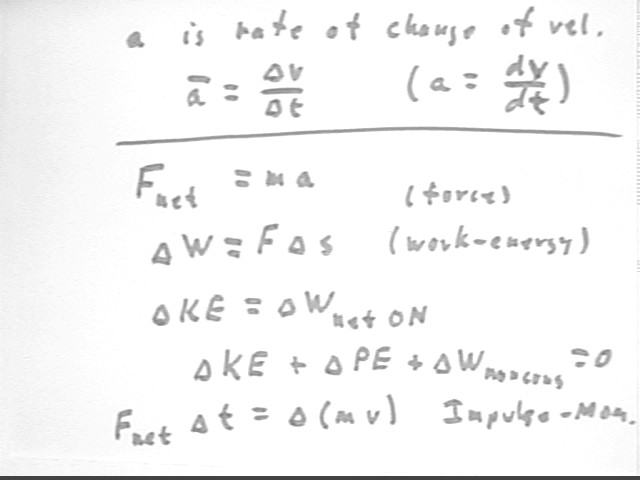
Force, work and momentum have the units indicated below:
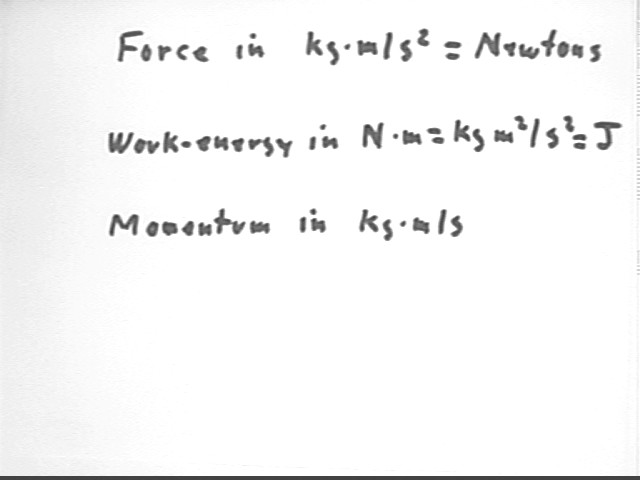
Experiment:
Roll a big marble down the 'track' and determine its velocity as it exits the ramp.
Take measurements needed to get change in gravitational PE down the incline (I'll give you the mass).
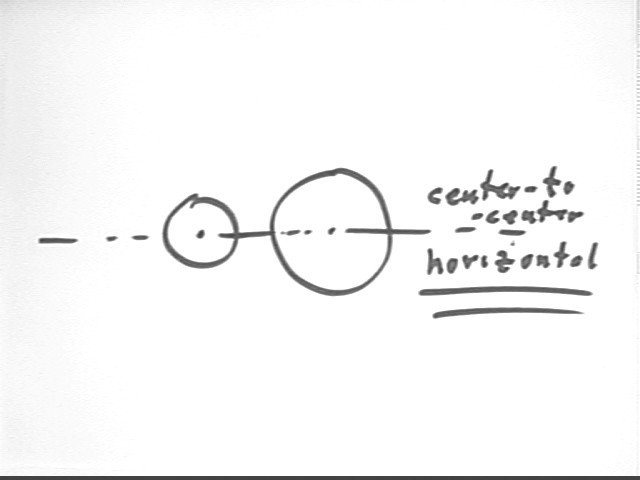
Collide the big marble with the pendulum marble so that immediately after collision both marbles are moving in the horizontal direction.
This is accomplished by ensuring that the center-to-center line between the two marbles is horizontal.
Take measurements to determine the after-collision velocity of the big marble and the pendulum marble. (The pendulum marble can be analyzed from the length of the pendulum and how far it is displaced from its equilibrium position as a result of the collision).
In the figure below `dx is the horizontal displacement of the pendulum, `dsx is the horizontal displacement of the large marble after collision, and `dy is the vertical displacement of the large marble as it rolls down the incline.
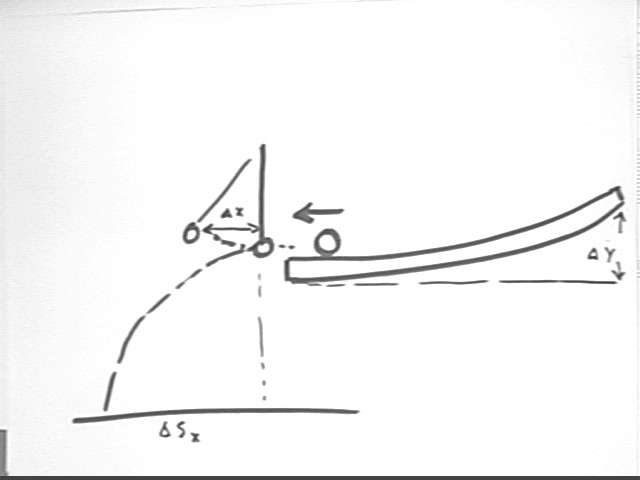
Measure the diameters of both marbles.
Analyze the momentum changes:
Find and list in a table the velocities of the big marble and the pendulum marble immediately before and immediately after collision. The velocity of the pendulum marble after collision can be determine from its PE change in a manner similar to that used in the quiz problem.
The mass of the big marble is 13 grams. The mass of the small marble is 13 grams * (d2 / d1)^3, where d1 and d2 are the diameters of the large and small marbles. Determine the mass of the small marble.
Determine the momentum of the large marble immediately prior to collision.
Determine the momentum of the small marble immediately after the collision.