Notes from Class 1016

Physics I Quiz 1016 

University Physics:  If force F(t) = 1000 t^3 N / s^3 acts on an object from t = 1 s to t = 2 s, by how much will the momentum of the object change?

As we saw in the quiz for the 10/14 class the area of a typical F vs. t trapezoid gives the approximate impulse during the time interval corresponding to the trapezoid.  This indicates that the impulse corresponds to the area under the graph, which is the definite integral of the given function.  So we integrate F(t) = 1000 t^3 N/s^3 with respect to t, from t = 1 to t = 2.

An antiderivative is 1000 t^4/4 N/s^3 = 250 t^4 N/s^3.  The change in this function from t = 1 sec to t = 2 sec is 

250 (2 sec) ^4 N/s^3 - 250 (1 sec)^4 N/s^3 = 3750 Newton seconds = 3750 kg m/s.

This is the desired change in momentum.

All students:

A marble of mass 13 kg, falling at about 4 m/s, lands on top of the fingernail of the index finger of a student whose finger is unfortunately already pressed to the floor.  The marble comes to rest as it travels a distance of 3 millimeters.  

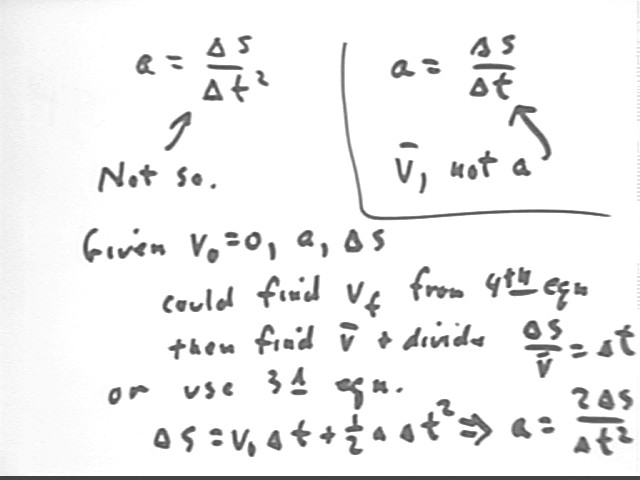
Note on serious errors in calculating acceleration:  Several quizzes indicated either a = `ds / `dt^2 or a = `ds / `dt.  Neither of these is correct.  `ds / `dt is velocity; the calculation doesn't even give units of acceleration.  

`ds / `dt^2 does give the right units but does not give acceleration in this situation.

We are analyzing vertical motion, characterized by v0 = 0, a = g = 9.8 m/s^2 and `ds = 60 cm.  This analysis requires use of the third and/or fourth equation of motion as indicated below.  The strategy of finding vf, then vAve and dividing vAve into `ds is familiar, having been used in numerous examples.

The third equation of motion `ds = v0 `dt + .5 a `dt^2, with v0 = 0, gives us `ds = .5 a `dt^2.  We easily solve for a, obtaining a = 2 `ds / `dt^2.  This is close to the asserted a = `ds / `dt^2, but it's not clear whether that assertion was made as a result of a valid analysis or something less enlightened.

The marble is shown below at initial contact with the finger.  The assumption of the problem is that the finger is compressed 3 mm by the impact.

The change in the momentum of the marble is easily found to be -.052 kg m/s.

Uniform accel allows us to find vAve by averaging init and final velocity, giving us vAve = 2 m/s.  At this average velocity the marble will come to rest in .0015 seconds.

The impulse-momentum theorem therefore tells us that the average force is about -35 Newtons.

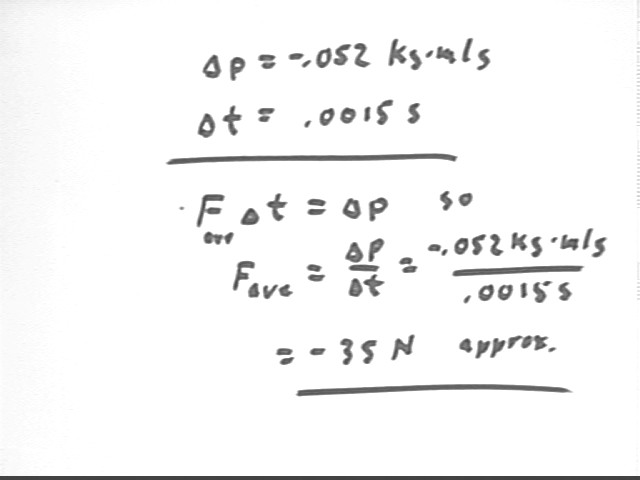
Do you think that the acceleration of the marble after contact with the finger would really be uniform?  What do you think the actual acceleration vs. clock time graph would look like?  Give a reasonable estimate of the maximum force exerted.

As the finger is compressed the force it exerts on the marble, which is equal and opposite the force exerted by the marble on the finger, will probably increase.  A graph of F vs. t will therefore probably be concave up.  The area under the curve must be .052 kg m/s, as would be the case for a linear graph (corresponding to constant acceleration).  The graph for the increasing force will have an increasing slope, so if the widths of the two graphs are the same its maximum slope would have to be greater than that for the linear situation, as would its maximum 'height', indicating a greater force.    However the time intervals (hence the widths) would be different for different force characteristics.  You should think about how this might affect the final conclusions.

All students:

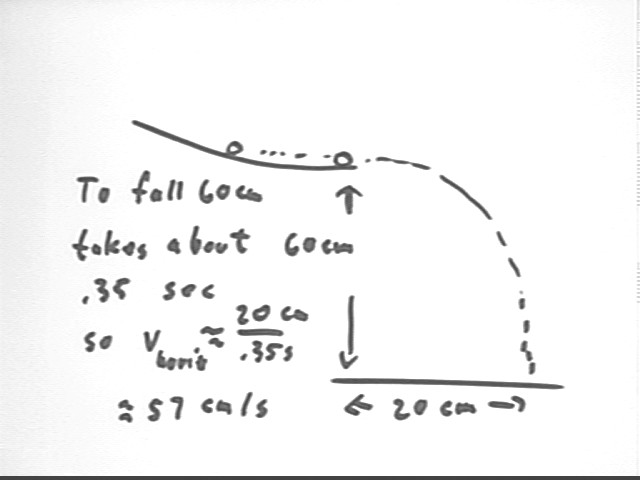
When a marble exits the incline with zero vertical velocity it falls to the floor 60 cm below as it travels in the horizontal direction for 20 cm.  When it collides with the pendulum just as it comes off the same incline, with the centers of the two marbles at the same vertical position, it travels only 8 cm in the horizontal direction as it falls.  What are the velocities of the marble just before and just after hitting the pendulum?

Using standard techniques of analysis we determine that the time of fall is about .35 second, giving us an average horizontal velocity of about 57 cm/s.

Similar analysis tells us that when the marble collides with the pendulum its horizontal velocity after collision is about 23 cm/s.

This allows us to compare the before-collision momentum of the large marble (based on the horiz velocity coming off the ramp) with the after-collision momentum (based on the horiz velocity after collision).  We find that the momentum changes by about -.004 kg m/s.

If a pendulum of length 13 cm, initially hanging at rest at equilibrium, is struck and as a result displaced to a maximum distance of 5 cm from its equilibrium position, then will be its speed when it returns to equilibrium?

To analyze the motion of the pendulum we will find from the given information the change `dy in its vertical coordinate, then use energy considerations to determine its velocity immediately after collision.

Constructing the indicated right triangle we find that at a 5 cm horizontal displacement from equilibrium the 13-cm pendulum is 12 cm below its support.  From this we conclude that the pendulum falls 1 cm as it swings back to its equilibrium position. 

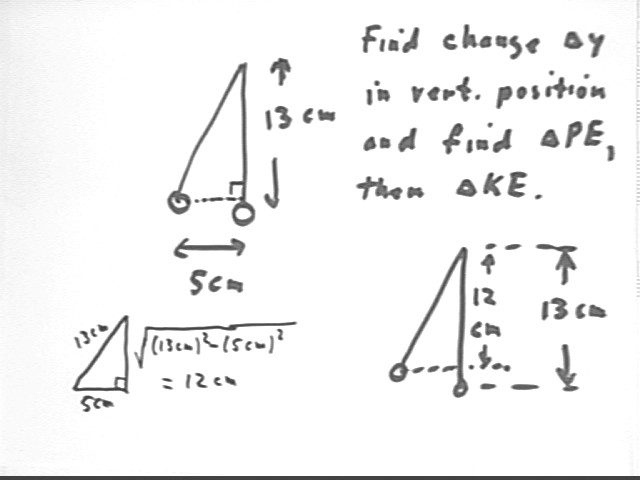
Using M for the mass of the pendulum we find `dPE in the fall back to equilibrium.  Then using energy conservation (note that `dWnoncons is presumably negligible here) we get vf = .32 m/s.

Energy considerations tell us that the pendulum must have had the same velocity immediately after collision (must have been so in order to have enough KE to increase its PE as its vertical position changes by +1 cm).

 

If we use m1 and m2 for the masses of the large and small marble, we can write expressions for the total momentum before and after collision (designated by pB and pA).  

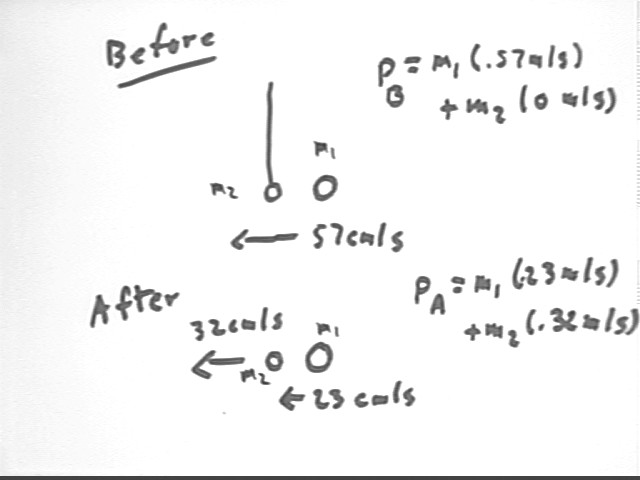
The total change in momentum must be zero, since the net force on the large marble and the net force on the small marble are equal and opposite and hence result in equal and opposite momentum changes.

Setting the total momentum before collision equal to the total momentum after collision we can solve for m2 / m1, obtaining m2 / m1 = 1.07 approx..  This would mean that the second (smaller) marble is 1.07 times as massive as the first, which would not be a very good result for this experiment.

Analysis of your actual data will likely give a more accurate result for the ratio of masses.

 

Experiment:  

Using three rubber bands with paperclips stretch the rubber bands out in the manner of the figure below, and mark the endpoints of each rubber band (as indicated by the circled points).

Sketch the line through the endpoints of each rubber band.  These lines will indicate the direction of the force exerted by each.

Sketch a y axis through the points of the rubber band which in this figure appears horizontal (the one to the right).

Sketch an x axis, perpendicular to the y axis, through the point at which the three lines of force meet.

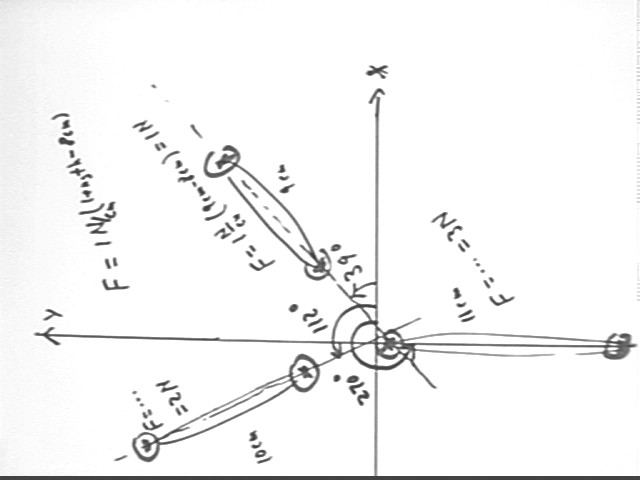
Turn the figure so that the y axis is pointing upward, and measure the angles made by the three lines of force with respect to the positive x axis.  The angles shown here are 39 deg, 112 deg and 270 deg..

Measure the length of each rubber band.  The lengths shown here are 9 cm, 10 cm and 11 cm.

Figure out the force on each rubber band, using F = 1 N / cm * (length - 8 cm).  For the lengths in the figure below this results in forces of 1 N, 2 N and 3 N.  Yours won't come out that nicely.

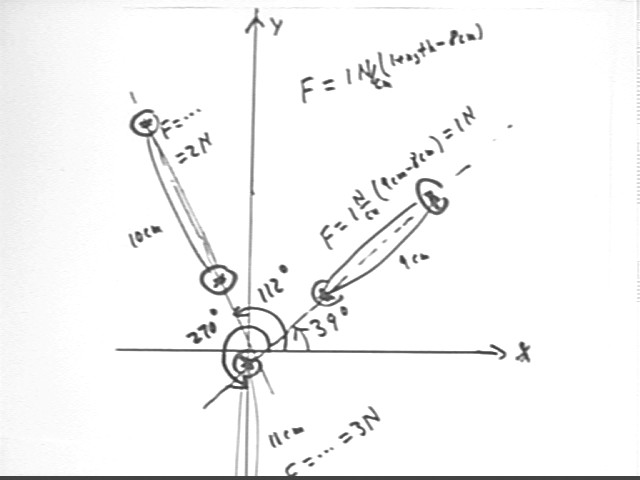
This will result in a figure like the one below, in which the forces are shown drawn to scale and all acting at the point of intersection.

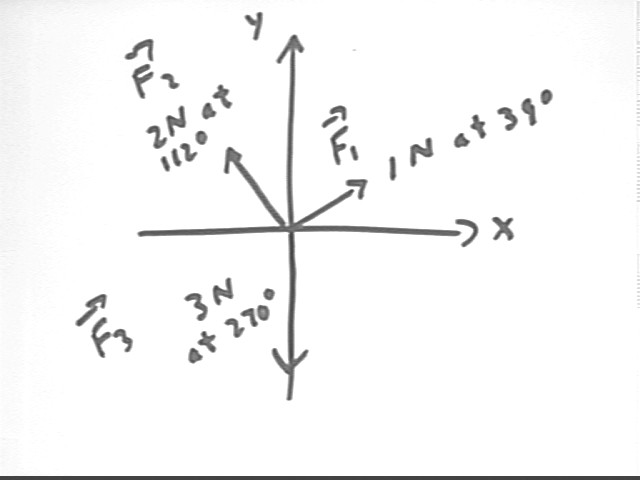
Make a table such as the one below.  Using your calculator calculate the x and y component of each force.

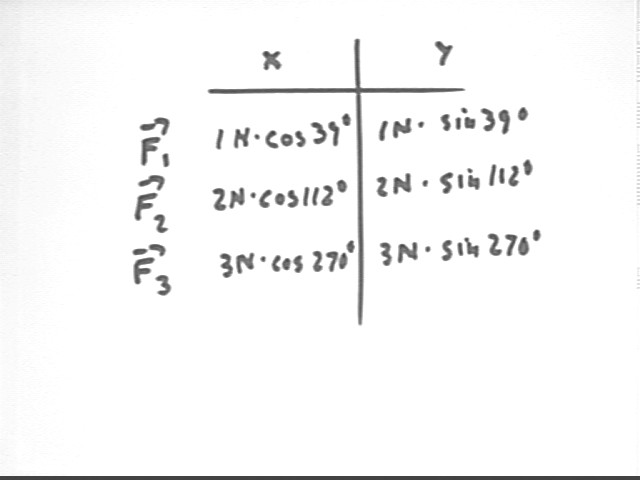
Add up the x components.  What do you get?

Add up the y components.  What do you get?

 

 

   

One day, all of the world's famous physicists decided to get together for a tea luncheon. Fortunately, the doorman was a grad student, and able to observe some of the guests...