Physics I Quiz 1021
University and General Physics: You are in an airplane moving at 200 m/s at an altitude of 10 km. The airplane is going to land, which requires that its speed be reduced to 50 m/s and its altitude to 0 km. What does conservation of energy tell you about what happens to the energy of your mass?
Whatever your mass we'll call it M. At the 10 km height your KE is .5 M (200 m/s)^2 = 20,000 m^2/s^2 * M. At landing your KE is .5 m (50 m/s)^2 = 1250 m^2/s^2 * M, so `dKE = 1250 m^2/s^2 * M - 20,000 m^2 / s^2 * M = -18,750 m^2/s^2 * M.
Your change in PE is weight * change in altitude = M g * (-10 km) = M * 9.8 m/s^2 * -10,000 m = -98,000 m^2/s^2 * M.
Thus the total energy of your mass changes by `dKE + `dPE = -18,750 m^2/s^2 * M - 98,000 m^2/s^2 * M = -116,750 m^2/s^2 * M.
Since `dKE + `dPE + `dWnoncons = 0 we have `dWnoncons = - ( `dKE + `dPE ) = - ( -116,750 m^2 / s^2 + M) + + 116,750 m^2 / s^2 * M.
The conclusion is that the airplane does positive work against the total of all nonconservatives forces. Air is the only thing touching the airplane, so this work must be done against air resistance. The airplane has to do a tremendous amount of work against air resistance to fall while slowing. This is accomplished by changing the configuration of the wings and the angle of the airplane with horizontal in order to expose more wing area to the relative motion of the air..
The tension in the string of a pendulum making an angle of 10 degrees with the vertical is 20 Newtons. What angle does the pendulum make with horizontal? What are the horizontal and vertical components of the tension force? What must be the weight of the pendulum's mass? What is its acceleration back toward the equilibrium position?
An automobile with mass 1500 kg coasts down an incline which makes an angle of 10 degrees with horizontal. Construct a right-handed coordinate system with the x axis parallel to the incline and a y axis perpendicular to the x axis. What angle does the automobile's weight make with the positive x axis? What therefore are the x and y components of the automobile's weight? What must be the normal force exerted by the incline on the automobile? If the coefficient of rolling friction is .02, and if air resistance is considered negligible, then what is the acceleration of the automobile?
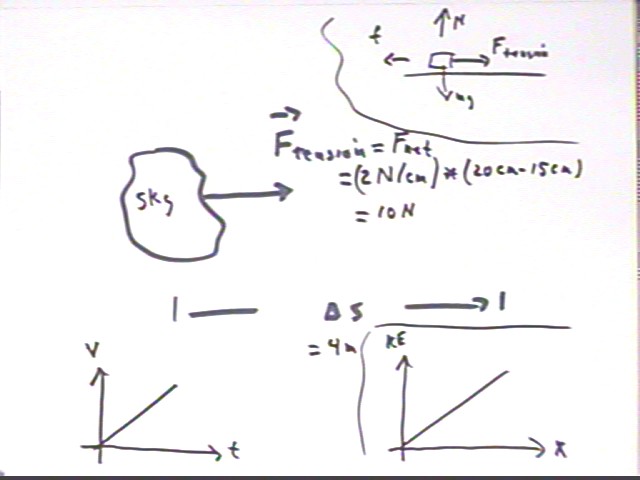
1. A stretched rubber band exerts a constant force on an object as it travels a given distance.
· A rubber band which exerts 2 Newtons of force for every cm in excess of length 15 cm maintains a length of 20 cm as it accelerates a mass of 5 kg from rest through a distance of 4 meters. All forces except the tension of the rubber band add up to zero.
2. A stretched rubber band exerts a constant force on an object for a given time interval
·
A rubber band which exerts 2 Newtons of force for every cm in excess of
length 15 cm maintains a length of 20 cm as it accelerates a mass of 5 kg from rest from t
= 0 to t = 4 seconds. All forces except the
tension of the rubber band add up to zero.
3. An object coasts down
an incline.
4. A pendulum is pulled
back and released.
5. A mass m1 rests on a
tabletop and it attached to mass m2 suspended by a string over a pully.
6. Masses m1 and m2 are
suspended from the same string over a pulley.
7. An automobile goes up
(or down) a hill.
8. A pumpkin fired from a
cannon strikes a moving car head-on.
9. An object moving in the horizontal direction begins to fall freely.
Definitions:
· vAve = `ds / `dt
· a = `dv / `dt
If acceleration is uniform vAve = (v0 + vf) / 2 * `dt.
The four equations of uniformly accelerated motion
· `dW = F * `ds
· KE = .5 m v^2
· `dPE = work done against a conservative force.
· PEgrav = m g y
· PEspring = .5 k x^2
· p = m v
·
impulse = Fnet * `dt
Laws:
· Newton's Laws (inertia, F = m a, action-reaction)
·
Conservation of energy (follows from 4th equation of motion and Newton's 2d
Law):
`dKE + `dWnet = 0 (basic form)
`dKE + `dPE + `dWnoncons = 0 (breaking `dWnet into `dPE
and `dWnoncons)
·
Impulse-Momentum and Conservation of momentum (follows from 2d equation of
motion and Newton's 2d Law)
Fnet * `dt = `dp
m1 v1 + m2 v2 = m1 v1 ' + m2 v2 '
Problem-solving Procedure
·
List all forces acting on the system
and sketch to scale, listing all known magnitudes and directions.
· If forces act in more than 1 dimension
resolve all forces into components relative to an appropriate coordinate system.
· v0, vf, `ds, `dt, a, `dv, vAve
· m, F, Fnet
· KE0, KEf, `dKE, `dPE, `dWnoncons
· `dp, p1, p2, impulse
Identify the system and note conserved quantities and
the laws of physics:
· Newton's first, second and third laws.
· Conservation of energy.
· Conservation of momentum.
Think about what you've got:
· Identify the units of each quantity.
· Relate each quantity to experience or
experiment.
· Graph everything you can.
· Identify relationships among given,
desired and derivable quantities.
Assemble your information and relate to the situation:
· Find all possible derivable quantities.
· Relate your results to the situation
and if anything is missing find it.
Apply these procedures to the following situations:
1.
A
rubber band which exerts 2 Newtons of force for every cm in excess of length 15 cm
maintains a length of 20 cm as it accelerates a mass of 5 kg from rest through a distance
of 4 meters. All forces except the tension of
the rubber band add up to zero.
The length in excess of 15 cm is 20 cm - 15 cm = 5 cm, so the force is 5 cm * 2 N/cm = 10 N. `ds is 4 meters; in the absence of other information we assume that `ds and F are in the same direction. We note that since all other forces add up to zero the net force is equal to the rubber band force.
We also note that the mass of the object is 5 kg.

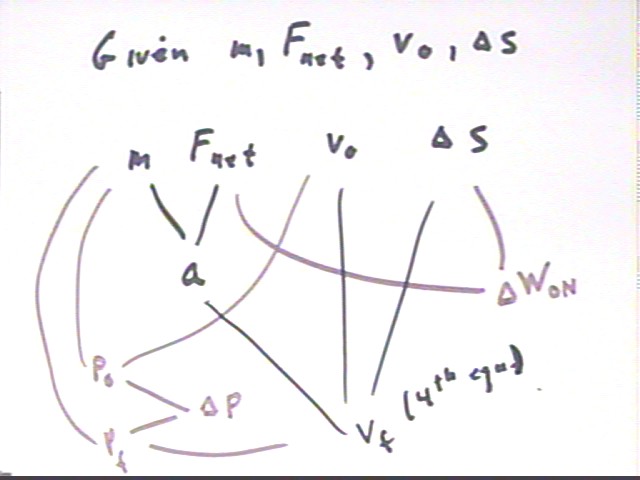
Knowing m and Fnet we can find a, which could then be combined with v0 and `ds to obtainf vf using the 4th equation of unif accel motion. It isn't indicated on the figure but v0 and vf could then be used to get vAve, which could be combined with `ds to get `dt.
We also note that m and v0 give us initial momentum p0, and m and vf give us final momentum pf; combining these we get `dp, the change in momentum. It isn't shown but `dp, which is equal to impulse, and Fnet can be combined using the impulse momentum theorem to give us `dt.
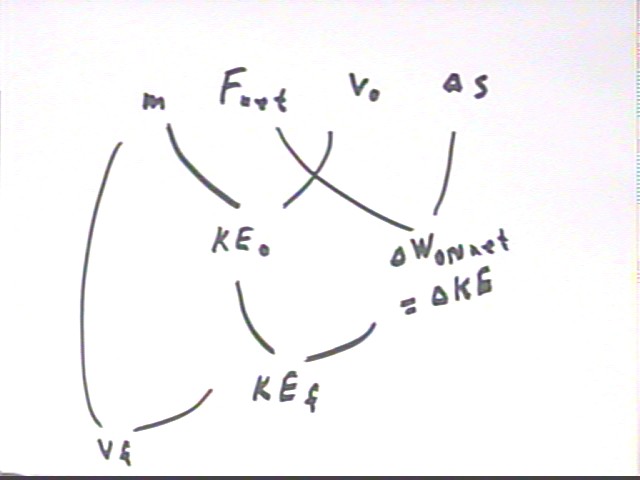
Fnet and `ds could give us the work done on the system by the net force. In the second figure below we isolate this part of the diagram and note that the work done on the system by the net force is `dKE. From m and v0 we have KE0, so which we can combine with `dKE to get KEf. Combining knowledge of KEf and m then gives us vf.
2.
A rubber band which exerts 2 Newtons of
force for every cm in excess of length 15 cm maintains a length of 20 cm as it accelerates
a mass of 5 kg from rest from t = 0 to t = 4 seconds.
All forces except the tension of the rubber band add up to zero.
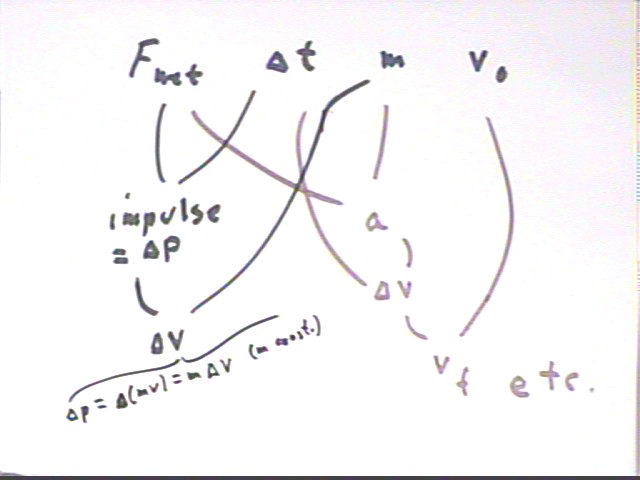
We sketch the situation below, showing an object with net force Fnet = 10 N. Listing the given quantities we have Fnet = 10 N, v0 = 0, `dt = 4 sec, m = 5 kg.
We can from the given information determine the impulse Fnet `dt of the net force.

The diagram indicates how Fnet and `dt give us impulse, which is equal to `dp. From `dp and the constant mass we easily determine `dv and indicated.
We could alternatively combine Fnet with m to get acceleration a, which with `dt gives `dv, which can be combined with v0 to get vf.
3. A bicycle and its rider with a total mass of 100 kg coast from rest for a distance of 5 meters down an incline at 30 degrees with respect to horizontal. The coefficient of friction between bicycle and incline is .02 and air resistance is considered negligible.
The figure below depicts a mass, repesenting but not looking like the bicycle and rider, on a 30 deg incline. The forces on the object include the weight m g, the normal force Fn perpendicular to the incline, the frictional forces fAir of air resistance and the force fSurface of surface friction both act in the direction opposite motion. `ds = 5 meters and coefficient of friction `mu = .02 are also indicated.
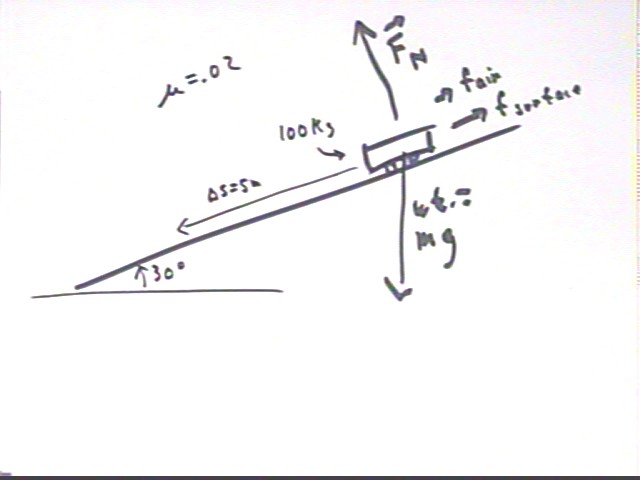
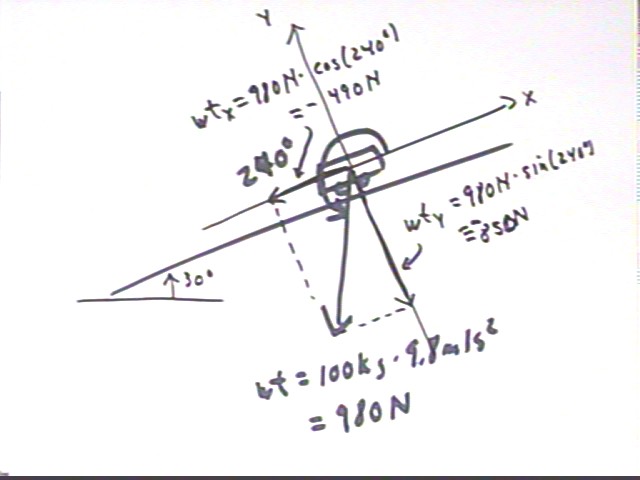
We construct a coordinate system with the x axis parallel to the incline and the y axis perpendicular. This system has the advantage that, since we know all the motion is in the x direction, we know that acceleration in the y direction is zero and that the forces in the y direction therefore add up to zero.
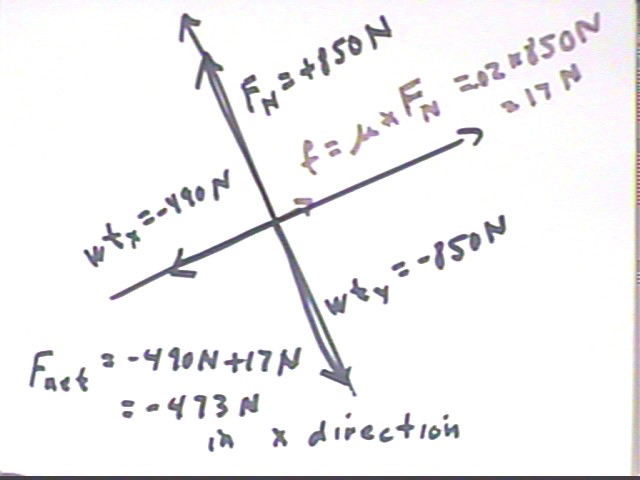
All forces except the weight act in the x direction. We find the components of the weight. Noting that inclining the x axis at 30 degrees above horizontal rotates the y axis from its usual vertical to an angle of 30 degrees with vertical, we find that the weight acts at an angle of 240 deg as measured counterclockwise from the positive x axis. We therefore obtain -490 N and -850 N, approx., for the x and y components of the weight.
The normal force Fn is the only force other than the weight acting in the y direction; since the net force in the vertical direction must be zero it follows that Fn = 850 N. From this and the coefficient of friction we find that the force of surface friction has magnitude .02 * 850 N = 17 N, which in this case acts in the direction up the plane--in the positive x direction as depicted here.
The net force in the x direction is therefore -490 N + 17 N = -473 N.
The diagram is not depicted here but from Fnet and the given `ds we can now determine `dWnet, the work done on the system by the net force, which is equal to the change in the KE of the system.. Since the system is as rest initial KE is zero we easily find the final KE. With the mass of the system we then find the final velocity vf.
Alternatively we could use the net force and the mass to find the acceleration of the system. Then knowing v0 = 0 and `ds we could find the final velocity using the fourth equation of motion.
Having found vf we can combine with v0 to get vAve, which with `ds gives us `dt.
Further problems:
A pendulum is pulled back
and released.
· A 5 kg simple pendulum of length 4
meters is pulled back .2 meters from its equilibrium position. The pendulum is then released.
A mass m1 rests on a tabletop and is attached to mass
m2 suspended by a string over a pully.
· A 5 kg mass on a table is attached by a
string over a pulley to a suspended mass of 2 kg. The
coefficient of friction between mass and table is .2.
The system is initially moving at .5 m/s in the 'forward and downward' direction,
and it moves 1.5 meters from this point.
· A 5 kg mass on a table is attached by a
string over a pulley to a suspended mass of 2 kg. The
coefficient of friction between mass and table is .2.
The system is initially moving at .5 m/s in the 'forward and downward' direction,
and it moves for 3 seconds starting from this point.
Masses m1 and m2 are suspended from the same string
over a pulley.
· Masses of 4 kg and 5 kg are suspended
by a string over a pulley. Friction exerts a
force equal to .1 times the total weight of the system, which is released from rest and
descends in the direction of the greater mass for 3 meters.
· Masses of 4 kg and 5 kg are suspended
by a string over a pulley. Friction exerts a
force equal to .1 times the total weight of the system, which given a velocity of 2 m/s in
the direction of the 4 kg mass. How far does
the system move before turning around and moving in the opposite direction?
A pumpkin fired from a cannon strikes a moving car
head-on.
· A 10 kg pumpkin moving at 900 mph
(about 400 m/s) collides head-on with a 1500 kg automobile traveling toward it at 30 m/s.