Physics I Quiz 1023
The tension in the string of a pendulum making an angle of 10 degrees with the vertical is 20 Newtons. What angle does the pendulum make with horizontal? What are the horizontal and vertical components of the tension force? What must be the weight of the pendulum's mass? What is its acceleration back toward the equilibrium position?
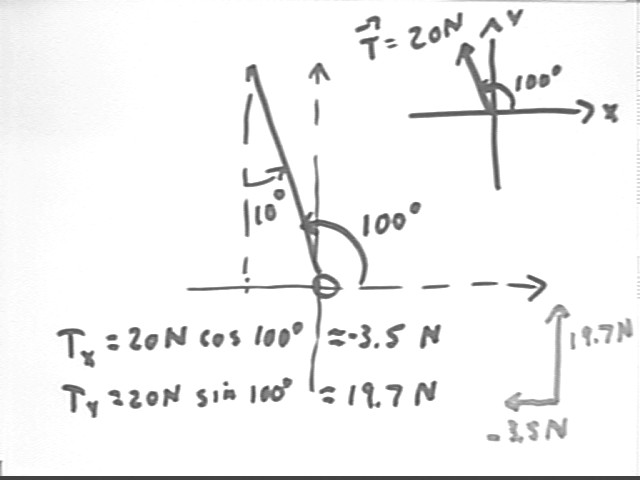
We first sketch the pendulum on a coordinate system with axes in the horizontal and vertical directions, as indicated below. As sketched the angle of the pendulum is seen to be 100 deg. It follows that the 20 N tension force is at 100 deg and that the x and y components are respectively -3.5 N and 19.7 N, approx..
The tension force is in all ways equivalent to the action of the two component forces. The two component forces are sketched at lower right.

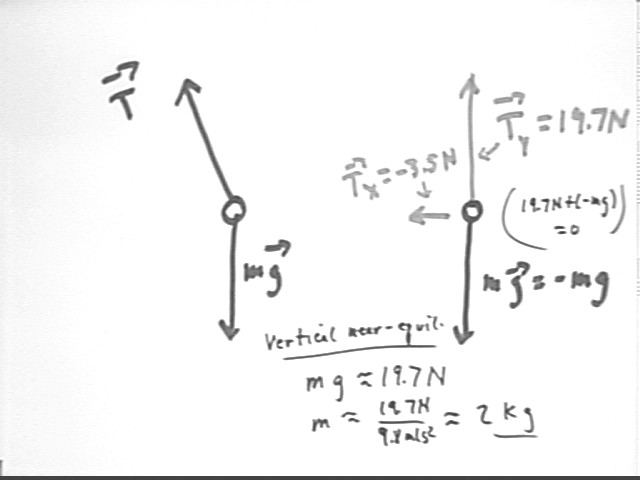
Since the string is nearly vertical already the pendulum won't descend much as it swings back toward equilibrium, so its vertical acceleration will be nearly zero. If the vertical acceleration was in fact zero we would have vertical equilibrium on the swing back. Since the acceleration is small but not quite zero we say that we have approximate equlibrium in the vertical direction.
It follows that the weight of the pendulum mass is nearly, though not quite, equal and opposite to the y component of the tension. So we have
net force = Ty - m g = 0 approx. and
m g = Ty approx.
Since we know g and Ty we can find m:
m = Ty / g = 14.7 N / (9.8 m/s^2) = 2 kg, approx.
Knowing the mass we can now find the acceleration in the x direction, which is
ax = Tx / m = -3.5 N / (2 kg) = -1.75 m/s^2.
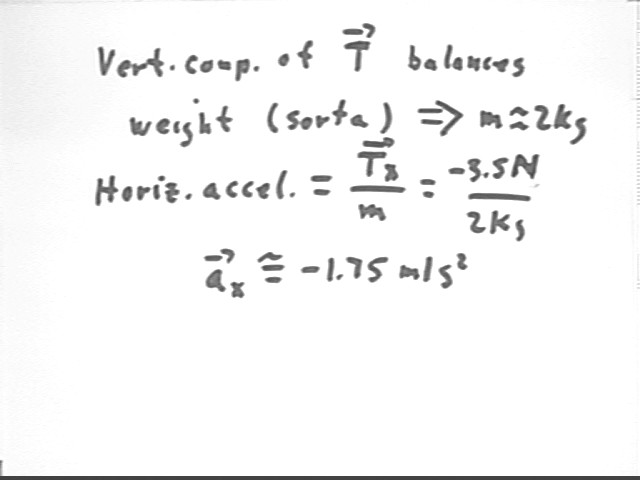
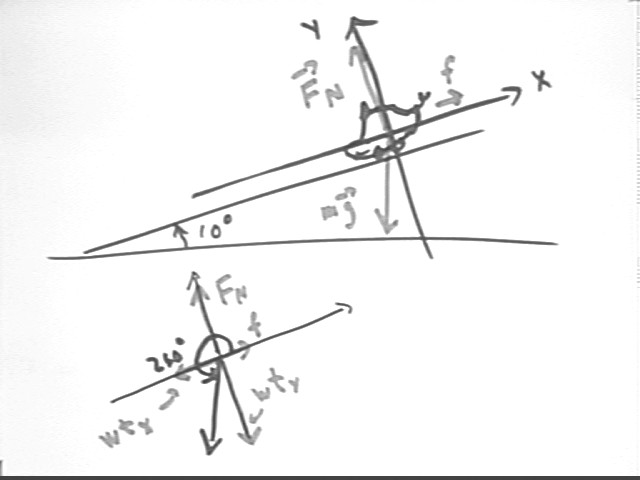
An automobile with mass 1500 kg coasts down an incline which makes an angle of 10 degrees with horizontal. Construct a right-handed coordinate system with the x axis parallel to the incline and a y axis perpendicular to the x axis. What angle does the automobile's weight make with the positive x axis? What therefore are the x and y components of the automobile's weight? What must be the normal force exerted by the incline on the automobile? If the coefficient of rolling friction is .02, and if air resistance is considered negligible, then what is the acceleration of the automobile?
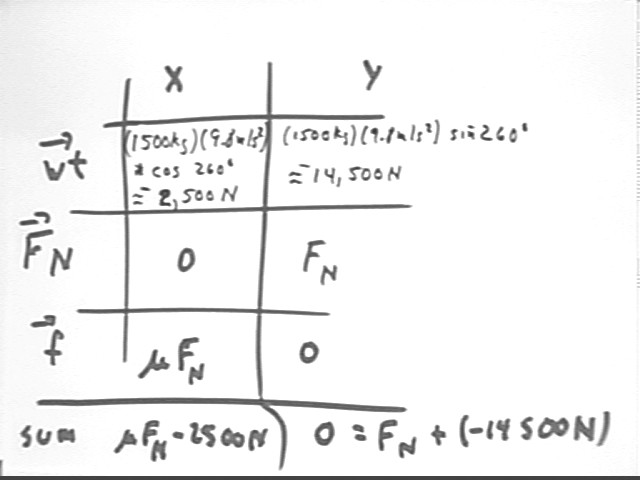
The sketch below depicts the automobile on the incline, with the x and y axes respectively parallel and perpendicular to the incline. The normal force Fn, the frictional force f and the weight force m g are depicted. The small graph at lower right depicts these same force, indicating the 260 deg angle of the weight vector with the positive x axis.
A table showing the x and y components of the three vectors shows x components 1500 kg * 9.8 m/s^2 * cos(260 deg) = -2500 N, approx., as well as 0 since Fn is along the y axis and therefore has zero as its x component, and `mu Fn, the frictional force which acts in the positive x direction.
The y components are 1500 kg * 9.8 m/s^2 * sin(260 deg) = -14,500 N, approx., as well as the entire force Fn, which is along the positive y axis, and o for the frictional force, which acts in the positive x direction with no y component.
Since we have equilibrium in the y direction (we have chosen our directions in such a way that the motion is all in the x direction, giving us a constant y velocity of 0 and therefore 0 acceleration in the y direction), we see that Fn + (-14,500 N) = 0 and that the net force in the x direction is the sum mu * Fn - 2500 N = FnetX.
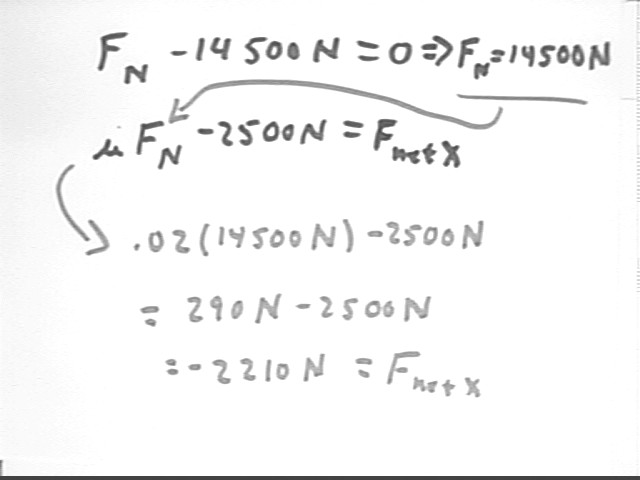
Our equation for y equilibrium tells us that Fn = 14,500 N.
Using this solution in the second equation we obtain a form which gives us FnetX = -2210 N.
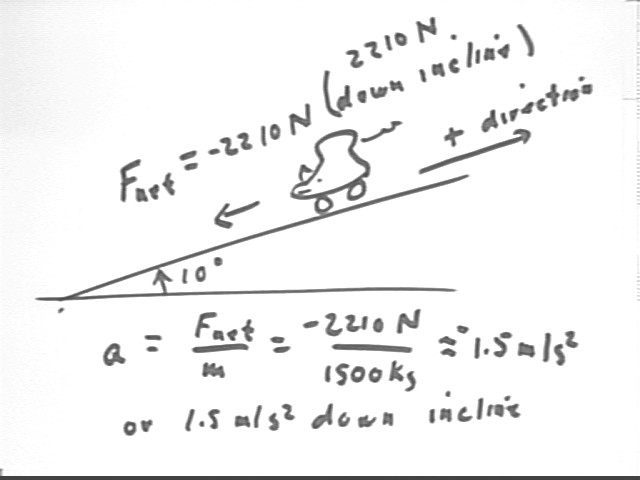
The result is that the sum of all the forces acting on the car is -2210 N down the incline, giving it an acceleration of a = F / m = -2210 N / (1500 kg) = -1.5 m/s^2, approx., down the incline.
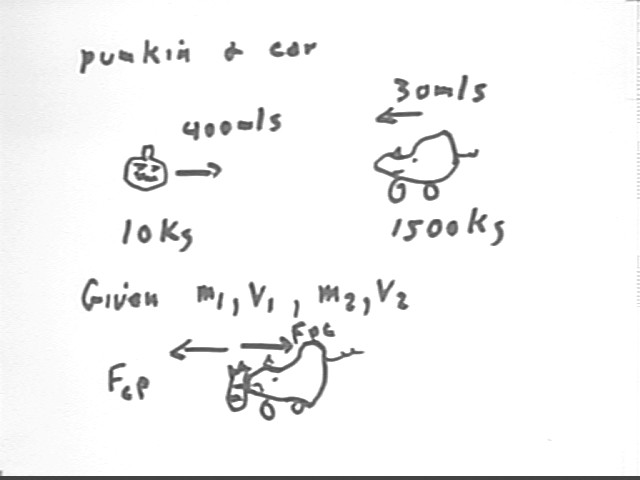
A 10 kg pumpkin moving at 900 mph
(about 400 m/s) collides head-on with a 1500 kg automobile traveling toward it at 30 m/s.
Determine all relevant quantities.
We know the initial velocities v1 = 10 m/s and v2 = -30 m/s and the masses m1 and m2. We should immediately recognize that we therefore have the momentum p1 = m1 v1 and p2 = m2 v2 of the two colliding object. We also know the momentum is conserved in a collision.
Looking briefly at the forces we see that during the collision a force Fcp is exerted by the car on the pumpkin and a force Fpc is exerted by the pumpkin on the car. These forces will be variable from the instant of first contact until the instant the pumpkin and the car arrive at a mutual velocity.
By Newton's Third Law the forces are equal and opposite: Fcp = - Fpc, and since both forces act at every instant during the collision it follows that `dt is the same for both, so that the impulses of the two forces are equal and opposite. From this it follows that the momentum changes are also equal and opposite, and that the total momentum of the car-pumpkin system remains constant. Thus total momentum before is equal to total momentum after collision.
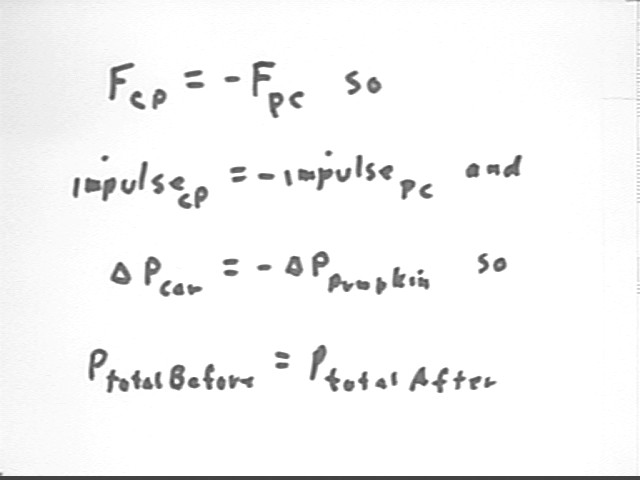
The total momentum before is p1 + p2 = m1 v1 + m2 v2 and the total momentum after is p1' + p2' = m1 v1' + m2 v2', where the ' indicates an after-collision quantity.
We also know that after collision v1' = v2' so we simply use v' for the common after-collision velocity. We obtain the equation
m1 v1 + m2 v2 = (m1 + m2) v', which we easily solve to obtain
v' = (m1 v1 + m2 v2) / (m1 + m2).
Substituting the given values of m1, m2, v1 and v2 (and using the rightward direction as positive) we get
v' = ( 10 kg * (400 m/s + 1500 kg * (-30 m/s) ) / (10 kg + 1500 kg)
= ( 4000 kg m/s - 75,000 kg m/s) / (1510 kg)
= -71,000 kg m/s / (1510 kg)
= -27.3 m/s, approx..
Looking at each step of the solution we recognize the following:
The numerator of ( 4000 kg m/s - 75,000 kg m/s) / (1510 kg) represents the 4000 kg m/s momentum of the pumpkin and the -75,000 kg m/s momentum of the automobile before collision and the denominator represents the 1510 kg total mass of the system.
-71,000 kg m/s / (1510 kg) represents the total momentum of the system, which applies after as well as before the collision, divided by the total mass of the system.
= -27.3 m/s, approx. represents the final velocity of the car and the pumpkin.
The car's velocity changed by -27.3 m/s - (-30 m/s) = +2.7 m/s and the pumpkin's velocity change by -27.3 m/s - 400 m/s = -427.3 m/s. The pumpkin, with 1/150th the mass of the car, had 150 times as much momentum change (within roundoff errors).

Using a 4.9 N weight suspended from two rubber bands held perpendicular to one another we saw directly how increasing the angle of inclination of the x axis results in greater and greater force component in the x direction and lesser and lesser force component in the y direction.
The situation is depicted below for angle of inclination 15 degrees.
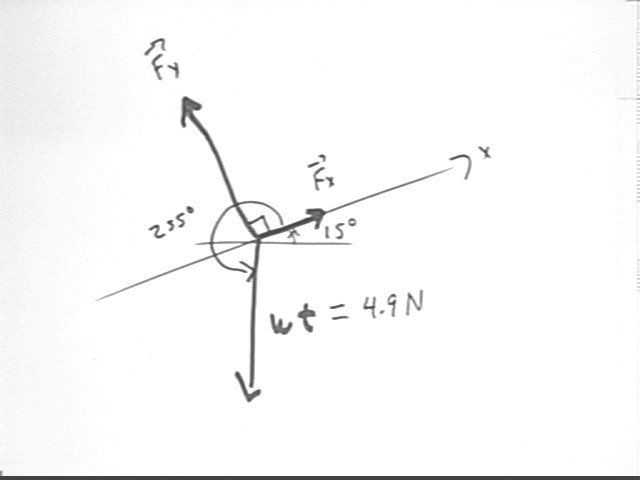
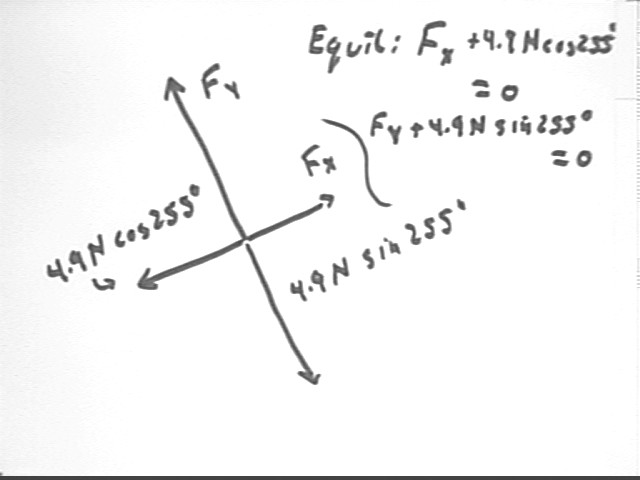
The tension forces in the x and y direction will be called Fx and Fy. The components of the weight in the x and y direction are easily calculated from the 255 deg angle and the known weight of 4.9 N.
Since the system was stationary its velocity was constant so the system was in equilibrium. Thus Fx will be equal and opposite to the x component of the weight and Fy will be equal and opposite to the y component of the weight.
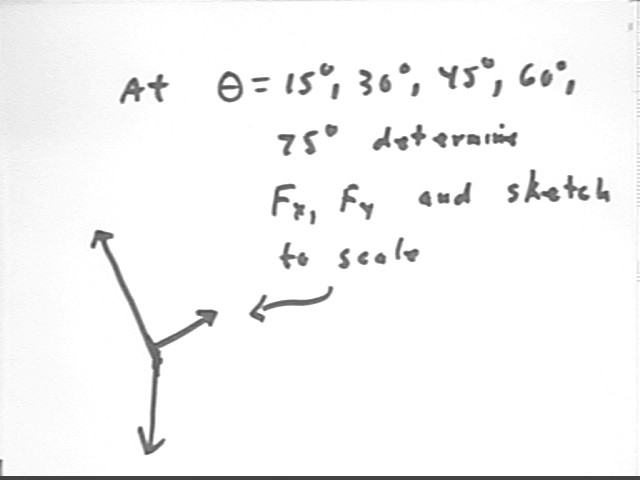
In preparation for an experiment to be performed during the next class period, determine the forces Fx and Fy required to support a 4.9 Newton weight at the given angles of inclination of the x axis.
Apply the problem-solving procedure outlined during the last class to the following situations:
A pendulum is pulled back
and released.
· A 5 kg simple pendulum of length 4
meters is pulled back .2 meters from its equilibrium position. The pendulum is then released.
A mass m1 rests on a tabletop and is attached to mass
m2 suspended by a string over a pully.
· A 5 kg mass on a table is attached by a
string over a pulley to a suspended mass of 2 kg. The
coefficient of friction between mass and table is .2.
The system is initially moving at .5 m/s in the 'forward and downward' direction,
and it moves 1.5 meters from this point.
· A 5 kg mass on a table is attached by a
string over a pulley to a suspended mass of 2 kg. The
coefficient of friction between mass and table is .2.
The system is initially moving at .5 m/s in the 'forward and downward' direction,
and it moves for 3 seconds starting from this point.
Masses m1 and m2 are suspended from the same string
over a pulley.
· Masses of 4 kg and 5 kg are suspended
by a string over a pulley. Friction exerts a
force equal to .1 times the total weight of the system, which is released from rest and
descends in the direction of the greater mass for 3 meters.
· Masses of 4 kg and 5 kg are suspended
by a string over a pulley. Friction exerts a
force equal to .1 times the total weight of the system, which given a velocity of 2 m/s in
the direction of the 4 kg mass. How far does
the system move before turning around and moving in the opposite direction?
A pumpkin fired from a cannon strikes a moving car
head-on.
· A 10 kg pumpkin moving at 900 mph
(about 400 m/s) collides head-on with a 1500 kg automobile traveling toward it at 30 m/s.