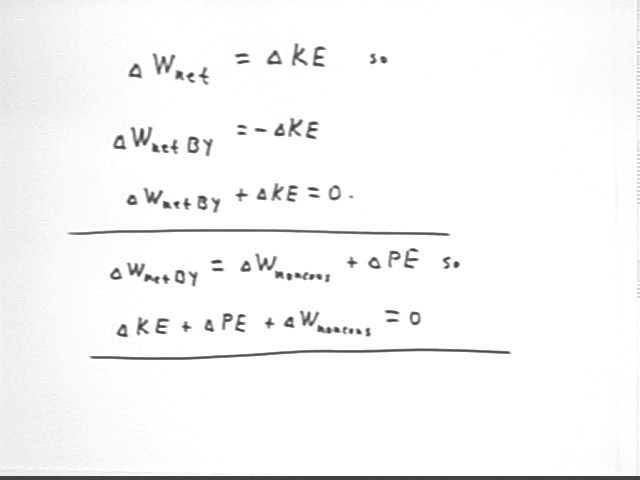Notes from Class 1025

Physics I Quiz 1025

Determine the forces Fx and Fy required to support a 4.9 Newton weight given that the angle of inclination of the x axis is 20 degrees.

Apply the problem-solving procedure outlined during the last class to the following situations:

A pendulum is pulled back and released.  

·     A 5 kg simple pendulum of length 4 meters is pulled back .2 meters from its equilibrium position.  The pendulum is then released.  

A mass m1 rests on a tabletop and is attached to mass m2 suspended by a string over a pully.  

·     A 5 kg mass on a table is attached by a string over a pulley to a suspended mass of 2 kg.  The coefficient of friction between mass and table is .2.  The system is initially moving at .5 m/s in the 'forward and downward' direction, and it moves 1.5 meters from this point.

·     A 5 kg mass on a table is attached by a string over a pulley to a suspended mass of 2 kg.  The coefficient of friction between mass and table is .2.  The system is initially moving at .5 m/s in the 'forward and downward' direction, and it moves for 3 seconds starting from this point.  

Masses m1 and m2 are suspended from the same string over a pulley.  

·     Masses of 4 kg and 5 kg are suspended by a string over a pulley.  Friction exerts a force equal to .1 times the total weight of the system, which is released from rest and descends in the direction of the greater mass for 3 meters.

·     Masses of 4 kg and 5 kg are suspended by a string over a pulley.  Friction exerts a force equal to .1 times the total weight of the system, which given a velocity of 2 m/s in the direction of the 4 kg mass.  How far does the system move before turning around and moving in the opposite direction?  

A pumpkin fired from a cannon strikes a moving car head-on.  

·     A 10 kg pumpkin moving at 900 mph (about 400 m/s) collides head-on with a 1500 kg automobile traveling toward it at 30 m/s.  

Experiment:

Determine the max unstretched length of a rubber band.

Using that rubber band fill the container until the rubber band suspending it exceeds its max unstretched length by 3 cm.

Suspend the container from each of the other rubber bands and determine by how much the length of each differs from its maximum unstretched length.

For angles theta = 15 deg, 30 deg, 45 deg and 60 deg:

Suspend the container from the original rubber band, and suspend this system from the other two rubber bands in such a way that

• The two rubber bands are at right angles.

• The angle with horizontal of the first of the two rubber bands is theta.

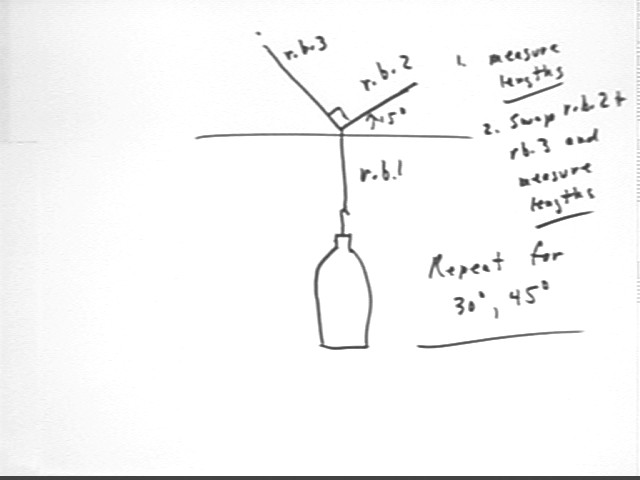
Measure the length of each of the two rubber bands.

Swap the two supporting rubber bands and measure the lengths again.

Assume that your rubber first band stretches by 1 cm for every .7 Newtons of tension.  Determine the weight of the bottle.

e.e., if the stretch in the first rubber band was 3.0 cm, then the weight of the bottle was .7 N / cm * 3.0 cm = 2.1 N)

How many Newtons of force does each of the other two rubber bands exerts per centimeter of stretch?

e.g., if the second rubber band had length 2.0 cm when supporting the bottle by itself, and if the weight of the bottle was 2.1 N, then the stretch of 2.0 cm resulted in a tension of 2.1 N and the force per cm is 2.1 N / (2.0 cm) = 1.05 N / cm.

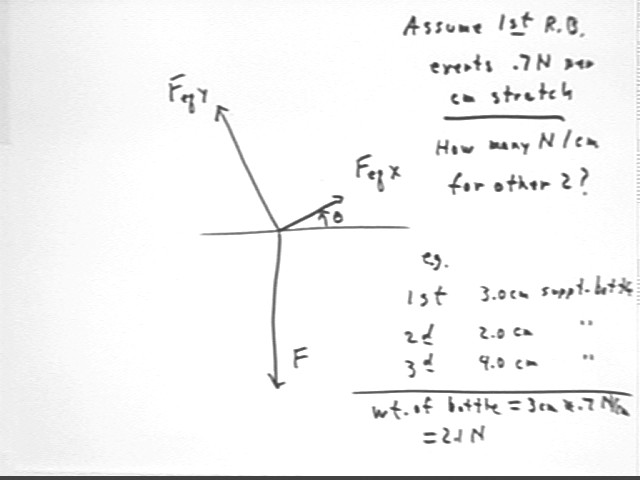
Determine the tension in each rubber band.

You will use the number of N / cm for the rubber band and the stretch of that rubber band in the specific situation you are analyzing.

Find the components in the directions of the other two rubber bands of the force exerted by the rubber band which directly supports the bottle. 

You will find the angle of the single supporting rubber band with the positive x axis (in the direction of the force labeled FeqX in the figure above) and the force of the single supporting rubber band (represented by F in the figure above) to find these components. 

How well do your results reconcile with the idea that the tension components of the first rubber band in the directions of the other two are equal and opposite to the forces exerted by those two rubber bands?

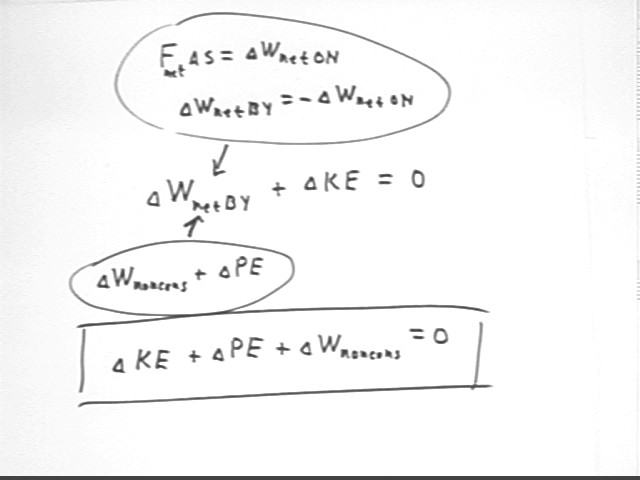
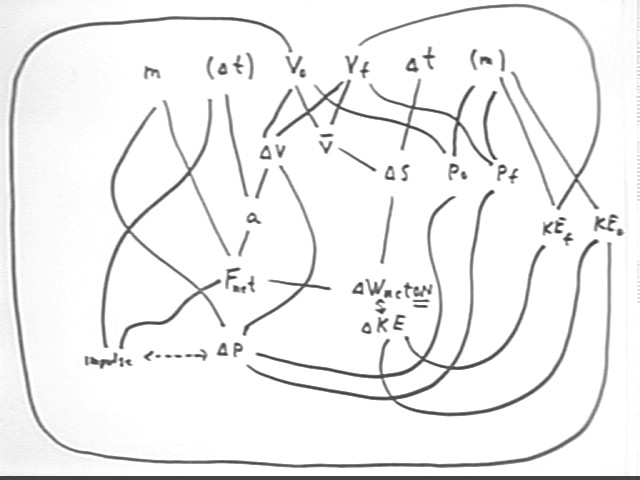
The figure shown below summarizes most of the quantities and relationships studied so far.  Each quantity is a vertex of at least one 'triangular' relationship.

The arrows between `dWnetON and `dKE, and between impulse and momentum, indicate that the two quantities connected by an arrow are equal.  These arrows therefore represent the Impulse-Momentum Theorem and hence the Law of Conservation of Momentum, and the original form of the Work-Energy Theorem.

You should look at each individual quantity, construct every triangle involving that quantity, write down the basic algebraic relationship between the quantities and a brief statement of how that relationship represents experience and common sense, and determine how that relationship allows us to find the quantity in terms of each of the other two.

You should also review the assigned problems to see how each one 'fits into' the diagram.

Your goal should be to be able to reconstruct this diagram whenever you need it.

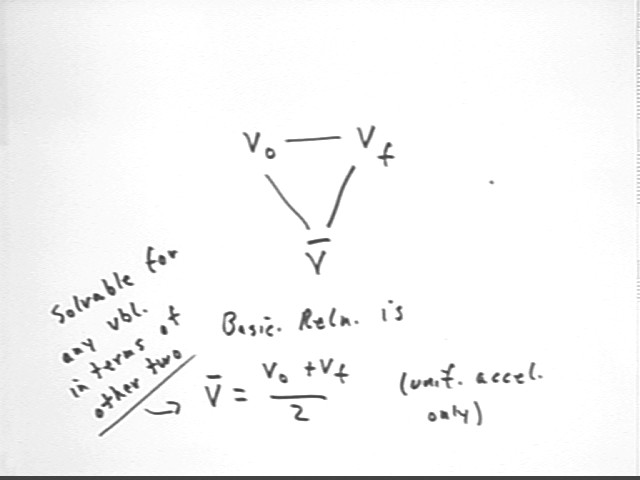
One possible triangle is the one shown below.  This triangle should be among those you construct for each of the variables v0, vf and `dt.

The defining relationship here is vAve = (v0 + vf) / 2, as indicated.  Note that this relationship applies only to uniformly accelerated motion.

This relationship is a direct result of the linearity of the v vs. t graph for unif accel motion.

The relationship is already solved for vAve; it is easily solved for either v0 or vf.  You should do this solution.

You should do a similar analysis for every 'triangle' in the larger diagram.

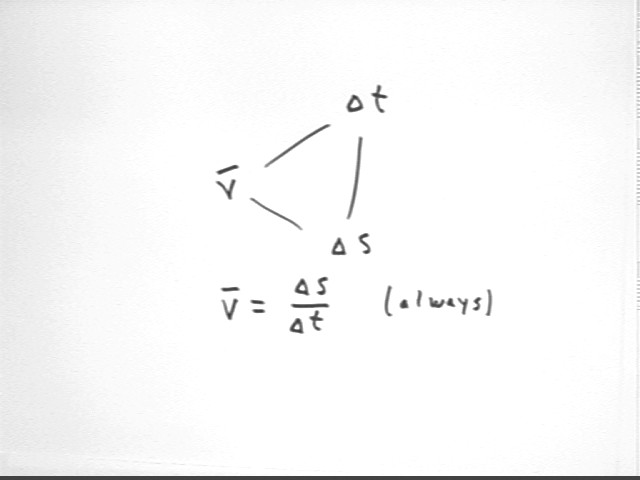
Another triangle involves vAve, `dt and `ds.  The defining relationship here is vAve = `ds / `dt, which holds in every situation.

The work-energy theorem as stated in the diagram says that Fnet `ds = `dWnetON, the work done by the net force ON the system BY the applied force F.  This is natural in the context of the diagram, where a is the accel of the system and Fnet is the net force exerted ON the system.

When we change our perspective to that of the system itself, we want to think in terms of the work done BY the system, which is the negative of the work done ON the system.  We have `dWnetBY = - `dWnetON, by Newton's Third Law.

From this it follows that `dWnetBy = -`dKE so that `dKE + `dWnetBY  = 0.  This is the second form in which we've seen the Work-Energy Theorem.

If we break the net force exerted by the system into forces exerted against conservative forces and forces exerted against nonconservative forces, we express the work done against all conservative forces as `dPE, the change in the PE of the system.  We use `dWnoncons (sometimes referred to in this context as just W) to represent the work done against all nonconservative forces.  This gives us the third breakdown of the Work-Energy Theorem:

`dKE + `dPE + `dWnoncons = 0.