Problem Number 1
By how much will the kinetic energy (abbreviated KE) of an object increase as a result of a net force of 540 Newtons exerted over a distance of 70 meters, assuming (ideally)that no energy is dissipated in the process?
Change in KE = work done by net force = 540 N * 70 m = etc.
Problem Number 2A displacement vector has length 2 and is directed at an angle with the positive x axis of 75 degrees. What are the displacements in the x and y direction which would give the same net displacement?
x component = magnitude * cos(theta)
y component = magnitude * sin(theta)
Problem Number 3What are x and y the components of the velocity vector obtained when we add the two following velocity vectors:
What are the magnitude and angle of the resultant vector?
resultant x component is Rx = Ax + Bx
resultant y component is Ry = Ay + By
Magnitude of resultant is sqrt(Rx^2 + Ry^2)
Angle of resultant is arctan(Ry/Rx), plus 180 deg if Rx is negative.
Problem Number 4Two objects collide and remain stuck together after collision.
One object has mass 13 kg and is moving in the positive direction at 11 m/s and the other has mass 13 kg and and moves at 20 m/s in the negative direction.
conservation of momentum tells us that
m1 v1 + m2 v2 = m1 v1' + m2 v2'.
We're given m1, m2, v1 and v2.
The objects stick together so v1' = v2'; use v ' for both v1 ' and v2 '.
m1 v1 + m2 v2 = m1 v' + m2 v' or
m1 v1 + m2 v2 = (m1 + m2) v' so
v ' = (m1 v1 + m2 v2) / (m1 + m2).
Problem Number 5
An object is pushed a distance of 13 meters by a force of 3 Newtons, with the force in the direction of the displacement.
`dW = F * `ds
Problem Number 6As an unknown force is exerted on an object of constant mass 18 kg its velocity is observed to change from 7 m/s to -35 m/s is 1 seconds.
Fave `dt = `dp.
`dp = m * `dv.
Solve for Fave.
From `dv and `dt find aAve.
Find Fave from m and aAve.
Problem Number 7An object of mass 15 kg experiences a variable force F(t) (here F(t) indicates function notation, not multiplication of F by t; F(t) is the force at clock time t) for .05 seconds.
If the average force over this time is 144 Newtons,
aAve = Fave / m
`dv = aAve * `dt.
Fave * `dt = `dp
`dp = m `dv.
Solve for `dv.
Problem Number 8An object with mass 6 kilograms, initially at rest, is acted upon by a force of 88.2 Newtons.
F `dt = `dp
`dp = m `dv
find `dv.
v0 = 0 so vf = 0 + `dv = `dv.
`dKE = .5 m vf^2 - .5 m v0^2
`dW = F `ds, where
`ds = (v0 + vf) / 2 * `dt
This result should be the same as that obtained in the previous step, by the Work-Energy Theorem.
Problem Number 9
A dense ball rolls off the edge of a cliff and follows a very nearly parabolic path to the floor.
At a certain instant the horizontal component of its velocity are, respectively, 7.87 meters per second and 3.84 meters per second.
v = sqrt(vx^2 + vy^2)
theta = arctan(vy/vx).
As we move closer to a planet its gravitational pull increases.
The more massive a planet is the greater its gravitational pull at a given distance.
Given two planets of the same density, one with greater radius, on which will you weigh more if you stand on its surface?
It will turn out that the gravitational field is essential 'spread out' over concentric spheres, making the field strength inversely proportional to the square of the distance from the center.
For two planets of equal density the planet's mass will be proportional to the cube of the planet's radius.
The net effect for a person standing on the surface is that the gravitational field is proportional to the cube of the planet radius and inversely proportional to the square of the planet radius. The result is that for planets of equal mass the field at the surface is proportional to the radius of the planet. The bigger planet has the greater gravitational field, and for example a planet twice the radius of another (with equal density) will exert twice the gravitational pull.
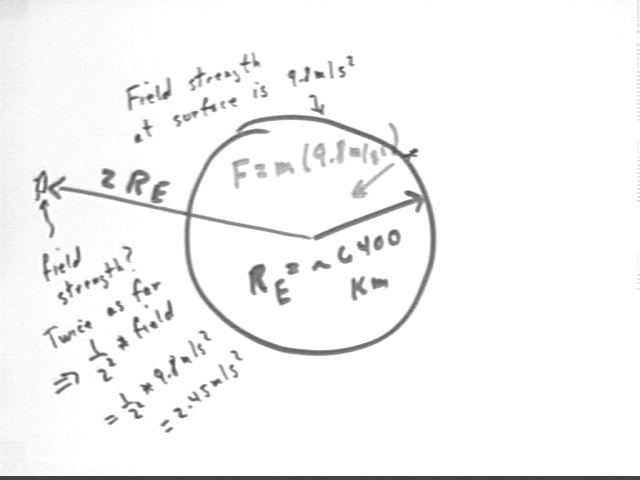
Earth's radius is about rE = 6400 km = 6,400,000 m and the gravitational field at its surface has strength 9.8 m/s^2.
By the inverse-square proportionality the field strength at double this distance is therefore 1 / 2^2 * 9.8 m/s^2 = 2.45 m/s^2.
A 75-kg person climbing a tower extending from the surface of the Earth to distance 2 rE will have to do a lot of work against gravity. At the start of the climb, near the surface, the gravitational field will exert a force of 75 kg * 9.8 m/s^2 = 734 Newtons, approx.. Near the end of the climb the field will exert a force o only 75 kg * 2.45 m/s^2 = 184 N, approx..
To get the average force we're tempted to average the maximum force, 734 N, with the minimum force, 184 N, to get an average force of 460 N, approx.. However the change in gravitational field, and therefore on gravitational force, is not linear with respect to position, but rather follows an inverse square proportionality. A graph of 1 / r^2 vs. r shows that the linear approximation very significantly overestimates the average force.
Using the erroneous approximation 460 N for the ave force we see that the work required is `dW = Fave * `ds = 460 N * 6,400,000 m = 3,000,000,000 Joules, approx..
It would take awhile for a 75 kg individual to produce that much excess energy. At the rate of 100 watts, or 100 Joules / second (sustainable by a 75 kg individual in very good physical condition), the time required would be about 1 year of continuous effort. Working only 8 hours per day, which is reasonable, the time required would be about 3 years.
