Physics I Quiz 1101
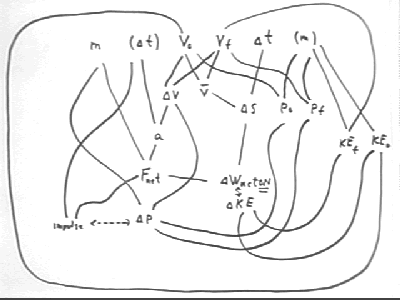
Using the 'map' distributed in class on 10/25, determine which 'triangles' correspond to each of the problems given below, and state the relationship for each 'triangle'.
If time permits construct a solution strategy based on the relationships you have identified.

An object moving at 9 m/s collides with an object moving at -6 m/s. After the collision the first object is observed to have velocity 1 m/s.
The mass of the first object is 4 kg and the mass of the second is 5 kg.
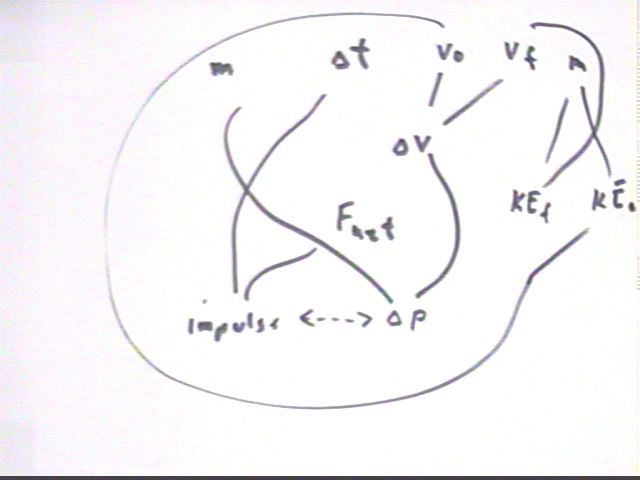
The situation here is a collision, so the beginning of our analysis is the impulse-momentum theorem, expressed in the picture as impulse < ------ > `dp. The figure below shows this part of the figure, along with the Fnet and the `dt we would put together to get the impulse.
Newton's Third Law tells us that the force exerted in the collision by the first object on the second is equal and opposite to the force exerted by the second on the first. For the short duration of a typical collision these equal and opposite forces greatly exceed any other forces acting on the objects and we therefore ignore all other forces, taking the net force on each object to be the force exerted on it by the other.
It follows that the impulses of the two forces are equal and opposite. The consequence of the impulse-momentum theorem is that the changes in momentum are therefore equal and opposite.

Setting `dp1 = - `dp2 and noting that for any object whose mass remains constant `dp = final momentum - initial momentum = m v' - m v we obtain the second equation
We are given the quantities m1, m2, v1, v1' and v2 so we can solve this equation for v2'. It is straightforward to substitute the known quantities to obtain v2'.
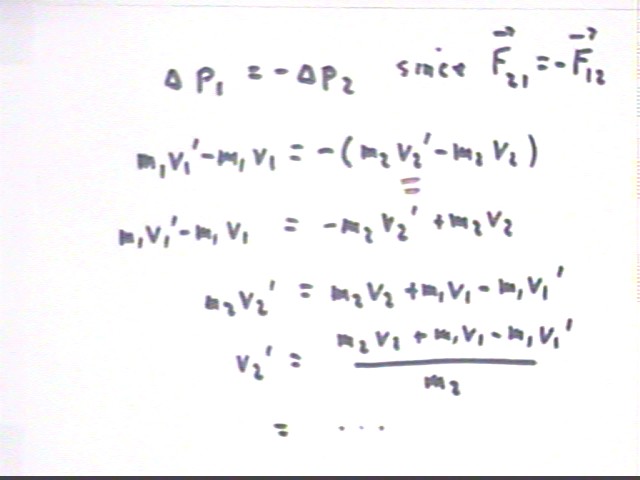
Problem Number 2
An object, initially at rest, is acted upon by a net force of 2600 Newtons.
Here we are given Fnet, m and `dt. These quantities are easily located in the 'map', and we see that Fnet and `dt give us the impulse, which is equal to the change `dp in momentum.
Combining `dp with m we get `dv, which we can combine with the known v0 to get vf. Combining these quantities with the known mass m we get KE0 and KEf, from which we will easily calculate `dKE.
Knowing `dt (given), v0 (given) and vf (calculated in the preceding) we can easily calculate vAve, which we multiply by the given `dt to get the object's displacement. This part of the 'map' is not depicted, since this is a standard procedure and the 'map' is already complicated enough.
Multiplying the given net force by the displacement of the object we get the work done by the net force.
If the calculations are done correctly the work done by the net force will equal the change in the KE.
Problem Number 3In order to stop a moving object, the object must be caused to expend a total of 144 Joules of energy.
The procedure here is straightforward and familiar. The 144 Joules of energy are expended if `dWnetBY = 144 Joules, so that `dWnetON = -144 Joules. So we know `dWnetON and `ds. If we locate these quantities on the 'map' we see that they form a 'triangle' with Fnet.
Of course we know from the definition of work that `dWnetBy = Fnet / `ds so Fnet will be 144 Joules / (8 meters) = 16 Newtons.

Gravitation
How much work is required to raise 75 kg from Earth's surface to 1000 km altitude?
At Earth's surface gravity exerts a downward force of 75 kg * 9.8 m/s^2 = 735 Newtons. To raise the object we gotta exert 735 Newtons against gravity, in the upward direction.
If this force didn't change, the work required would be 735 Newtons * 1000 km = 735 Newtons * 1,000,000 meters 735,000,000 Joules.
This is a bit of an overestimate, since gravitational acceleration decreases with altitude.
Using the inverse-square relationship we find that the acceleration of gravity at the 1000 km altitude is 7.33 m/s^2.
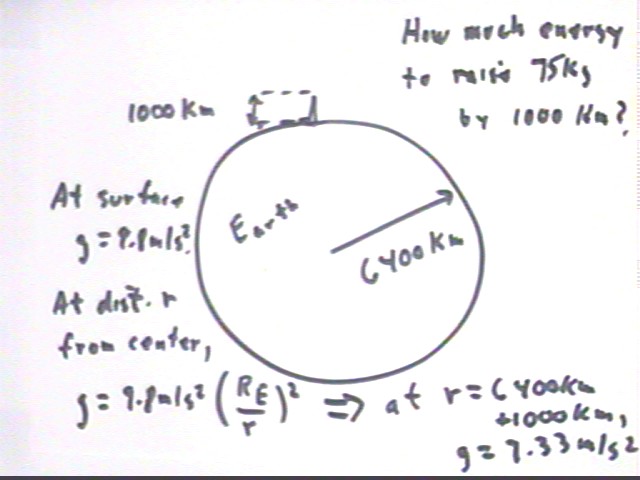
A graph of the magnitude of gravitational acceleration vs. distance r from the center of the Earth is depicted below. This graph is clearly nonlinear.
During the preceding class we averaged the forces at rE and 2 rE, which is equivalent to assuming a linear relationship. The straight line segment connecting the two corresponding graph points shows us that the linear assumption gives us an overestimate.
Between rE and rE + 1000 km, at which latter point the acceleration is about 7.3 m/s^2, we see that there is much less room for the graph to curve and that the graph is pretty close to linear, so averaging the two accelerations will give us a pretty good approximation.
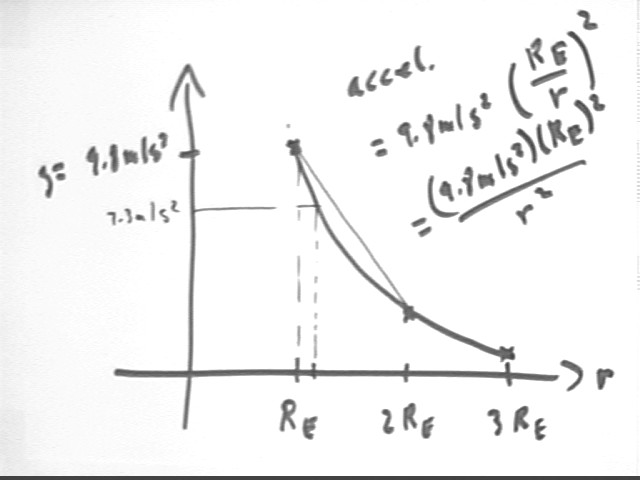
We get an approx. average of 8.57 m/s^2. If we modify our estimate of the work for this approximation we find that the total work is about 630,000,000 Joules.
Centripetal Acceleration
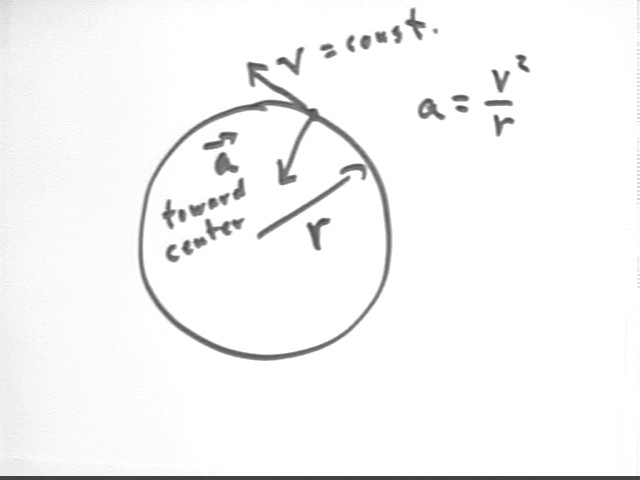
An object moving at velocity v on a circle of radius r has an acceleration toward the center of the circle which is equal to v^2 / r. This is called the centripetal acceleration of the object.
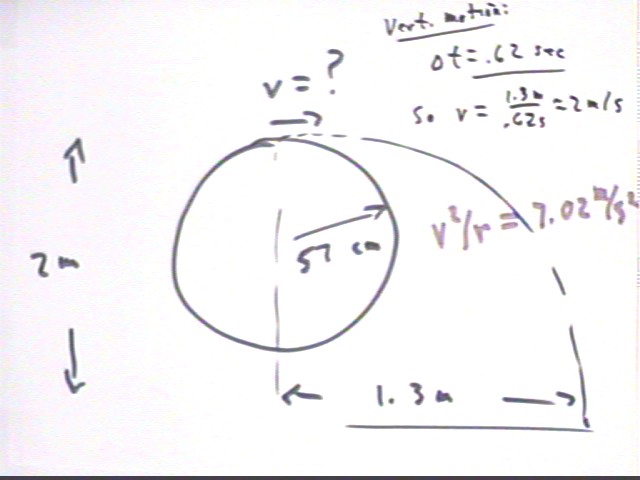
In class the instructor rotated a washer in a vertical circle of radius 57 cm, letting the string just barely go slack at the top of the arc and releasing the string at this point. The point of release was about 2 meters above the floor and the object traveled 1.3 m in the horizontal direction. Straightforward analysis yields time of fall `dt = .62 sec so that vHoriz = 1.3 m / (.62 s) = 2 m/s, approx..
This yields centripetal accel aCent = v^2 / r = (2 m/s)^2 / (.57 cm) = 7 m/s^2, approx..
The string having been slack, at the top of the arc the centripetal accel must have been 9.8 m/s^2 (since at the top gravity was the only force acting toward the center and the object was still traveling in a circular path). Our estimate of 7 m/s^2 is reasonable good confirmation of this fact.
To achieve a circular orbit of the Earth after climbing our tower we must attain just the right velocity parallel to the surface of the Earth. Too slow and we end up falling to Earth. As the velocity increases we travel further and further around the Earth, but only at a certain specific velocity do we make it all the way around to our starting point.
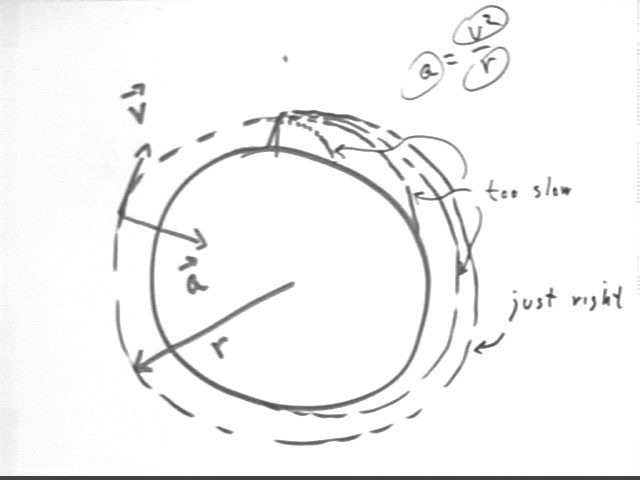
When we do in fact achieve circular orbit we will have a centripetal acceleration aCent = v^2 / r, which is supplied by gravity. At the 1000 km 'altitude' we have r = 6400 km + 1000 km = 7400 km or 7,400,000 m; and from our previous calculation we know that gravity is capable of supplying a 7.33 m/s^2 centripetal acceleration. This allows us to solve aCent = v^2 / r for v, giving us the speed necessary for a circular orbit at this 'altitude'.