Notes from Class 1104

University Physics Quiz 1104

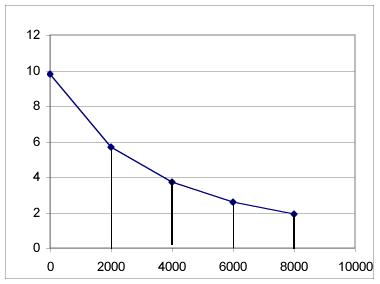
The approximate acceleration of gravity is given by the function g(y) = 9.8 m/s^2 * ( 6400 km / (6400 km + y) )^2.

This yields the approximate 'line graph' indicated below, representing acceleration vs. altitude for various 'altitudes' y.

Use the graph as appropriate to determine the approximate work required to 'lift' a 1 kg mass from the surface of the Earth to an 'altitude' of 8000 km.

The accelerations at 0, 2000 km, 4000 km, ... appear to be about 9.8 m/s^2, 5.8  m/s^2, 3.8 m/s^2, 2.7  m/s^2 and 2.0  m/s^2.

More accurate means tell us that these accelerations are in fact 9.8  m/s^2, 5.7 m/s^2, 3.7 m/s^2, 2.7 m/s^2 and 1.9  m/s^2.

For a 1 kg mass the graph also represents the number of Newtons of force exerted by gravity vs. 'altitude'.  We wish to find the work done for each interval of 'altitude'.  

Using the straight-line approximations we would get approximate average forces over the various 2000 km increments as follows:

The work over each interval is found by multiplying the 2000 km = 2,000,000 m corresponding to that interval by the approximate average force.  We get work contributions:

We can total these amounts to obtain total work about 36,000,000 J.

The calculations for the individual intervals correspond to ave altitude * width for each trapezoid, hence to trapezoid areas, which approximate the areas under the curve over the given intervals.

The 

Explain how you would use the g(y) function to determine the exact work done.

Physics I Quiz 1104

The table below gives the approximate acceleration of gravity at 'altitudes' of 2000 km, 4000 km, ..., 10000 km.

'altitude' (km) accel of gravity (m/s^2)
2000 5.7
4000 3.7
6000 2.6
8000 1.9
10000 1.5

What force would be required to 'lift' a 75 kg mass at 'altitudes' of 2000, 4000, 6000 and 8000 km.

Forces are about 428 N, 278 N, 195 N, 143 N.  Force at surface is about 734 N.

How much work would be done against gravity in lifting a 75 kg mass at constant velocity from the surface of the Earth to an altitude of 2000 km?

Force decreases from 734 N to 428 N as we lift thru the first 2000 km.  Approx. ave. force is (734 N + 428 N) / 2 = 580 N.  The approx. work is therefore `dW = F * `ds = 580 N * 2000 km = 580 N * 2,000,000 m = 1,160,000,000 Joules.

Ignoring air resistance how fast would the 75 kg object have to be 'shot' in the upward vertical direction in order to 'coast' to an altitude of 2000 km?

`dKE + `dPE = 0 since the only force acting on the object after the 'shot' is the gravitational force.  So `dKE = -`dPE = -1,160,000,000 J.

Intuitively, the object must be given enough KE that the KE can change it 1,160,000,000 Joules of PE.

Assuming that final KE is zero, then `dKE = KEf - KE0 = -KE0.

So -KE0 = -1,160,000,000 J and

.5 m v0^2 = 1,160,000,000 J so

v0 = +-sqrt(2 * 1,160,000,000 J / m) = +-sqrt(2 * 1,160,000,000 J / (75 kg)) = 5560 m/s.

How much work would be done against gravity in lifting the 75 kg mass at constant velocity from altitude 2000 km to altitude 4000 km?  

Forces at 2000 m and 4000 m are 428 N and 278 N, giving average force 353 N so that the work will be 353 N * (4000 km - 2000 km) = 706,000,000 J.

Ignoring air resistance how fast would the 75 kg object have to be 'shot' in the upward vertical direction from the surface of the Earth in order to 'coast' to an altitude of 4000 km?  

The total work required to 'lift' the object to 4000 km altitude is 

total work surface to 4000 km = work to raise to 2000 km + work to raise from 2000 km to 4000 km = 1,160,000,000 J + 706,000,000 J = 1,866,000,000 J.

The required velocity is again 

v0 = sqrt(2 * KE / m) = sqrt(2 * 1,866,000,000 J / (75 kg) ) = 7100 m/s, approx.. 

 

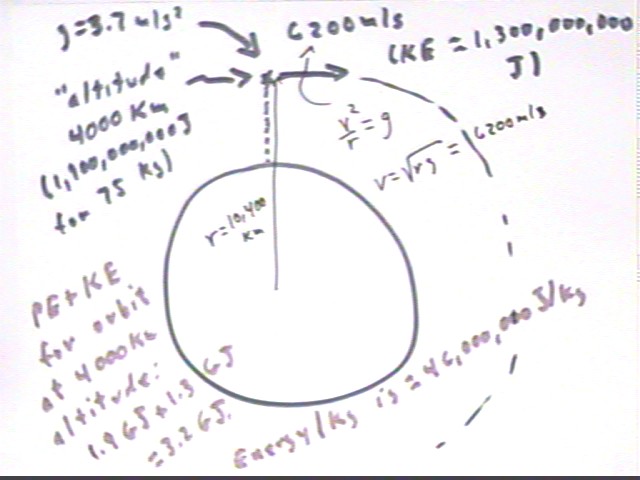
If the centripetal acceleration aCent = v^2 / r required to keep the object orbiting is provided by the Earth's gravitational attraction what must be the orbital velocity at the 4000 kg 'altitude', given that the Earth's diameter is 6400 km?

At 4000 km altitude the accel of gravity is about 3.7 m/s^2.  This is provided by the centripetal accl aCent = v^2 / r.  To get v we solve for v:

v = sqrt( aCent * r) 

At altitude 4000 km we have r = 6400 km + 4000 km = 10,400 km = 10,400,000 m.  So we get

v =  sqrt( 3.7 m/s^2 * 10,400,000 m) = sqrt(38,400,000 m^2/s^2) = 6200 m/s.

What is the total energy required to get the 75 kg object from the surface to a circular orbit at 4000 km 'altitude'?

The object will have KE = .5 * 75 kg * (6200 m/s)^2 = 1,300,000,000 Joules, approx..

It also has to have PE = 1,866,000,000 J so from the surface of the Earth to this orbit we need a total of

1,300,000,000 J + 1,866,000,000 J = 3,200,000,000 J.

This is for a 75 kg object.  How many joules do we need per kg?

We need 3,200,000,000 J / (75 kg) = 46,000,000 Joules / kg.

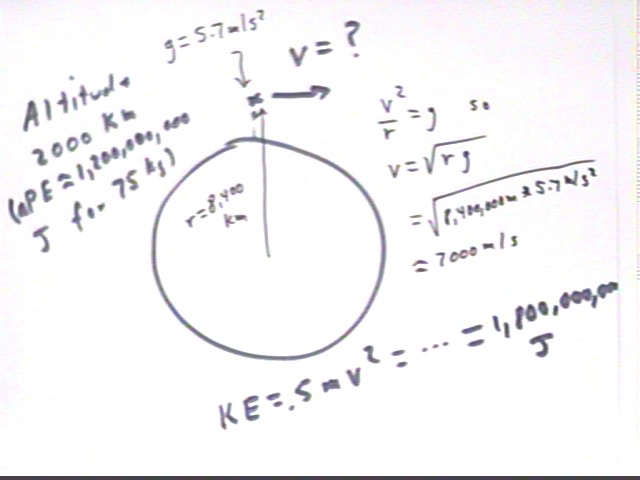
Compare orbit at altitude 4000 km with orbit at altitude 2000 km.  How much KE and how much PE is there at 2000 km?

Calculations similar to those done previously show us that orbital velocity is about 7,000 m/s, as opposed to 6200 m/s for the 4000 km 'altitude'.   This gives us KE of about 1,800,000,000 J at the 2000 km 'altitude'.  This is about 400,000,000 J greater than for the 4000 km altitude.

PE at the 2000 km 'altitude' was already found to be about 1,200,000,000,000 J, which is about 800,000,000 J less than the for 4000 km altitude.

Observe that the decrease in KE from the 2000 km to the 4000 km 'altitude' appears to be about half of the increase in PE. 

Note also that the change in total energy is `dPE + `dKE = 800,000,000 J + (-400,000,000 J) = +400,000,000 J.

How much work would be done against gravity in lifting the 75 kg mass at constant velocity from altitude 4000 km to altitude 6000 km, and from altitude 6000 km to altitude 8000 km?  Ignoring air resistance how fast would the 75 kg object have to be 'shot' in the upward vertical direction in order to 'coast' to an altitude of 8000 km?

The table below shows first the trapezoidal approximations to PE obtained by averaging the values of g at the begining and end of each interval, along with orbital velocity and KE results.  

The second part of the table, below the first, shows calculations based on Earth radius 6400 km and using integration of the force function f(y) = 1 kg * g(y) = 1 kg * 9.8 m/s^2 (6400 km / (6400 km + y))^2 to find PE.  Calculus students may note that an antiderivative of the f(y) function is -9.8 N (6400 km)^2 / (6400 km + y) and should be able, using the Chain Rule, to verify that this is an antiderivative..  

PE calculated by Trapezoidal Approximations of Orbital Energies per Kg, based on 2000-km intervals.

KE per kg calculated accurately (within roundoff error) from orbital velocity.
altitude y, km g in m/s^2 ave g for interval `dW / m per kg orbital vel m/s orbital KE / m in J per kg PE / m relative to surface, J KE / m change from next-lower orbit, J PE / m change from next-lower orbit, J ratio of KE change to PE change
0 9.8
2000 5.688889 7.744444 15488889 6912.79 23893333 15488889
4000 3.711243 4.700066 9400131 6212.642 19298462 24889020 -4594872 9400131 -0.48881
6000 2.610614 3.160928 6321857 5689.606 16185806 31210877 -3112655 6321857 -0.49236
8000 1.935802 2.273208 4546416 5279.731 13937778 35757293 -2248029 4546416 -0.49446
10000 1.492445 1.714124 3428247 4947.332 12238049 39185541 -1699729 3428247 -0.4958

 

Exact Calculations of Orbital Energies per Kg (PE from integral of force function, KE from orbital velocities, all accurate to 2 significant figures)

 
altitude y, km `dW / m per kg orbital vel m/s orbital KE / m in J per kg PE / m relative to surface, J KE / m change from next-lower orbit, J PE / m change from next-lower orbit, J ratio of KE change to PE change  
0
2000 14933333 6912.79 23893333 14933333
4000 9189744 6212.642 19298462 24123077 -4594872 9189744 -0.5
6000 6225310 5689.606 16185806 30348387 -3112655 6225310 -0.5
8000 4496057 5279.731 13937778 34844444 -2248029 4496057 -0.5
10000 3399458 4947.332 12238049 38243902 -1699729 3399458 -0.5

Note for University Physics students:

This question and answer applies generally to the calculation of work done by or against a varying force.

QUESTION FROM STUDENT:  I was working Text problem 6-65 last night when I found that I could get the right answer if I used a formula from the book, but it was one I did not exactly understand.

Ordinarily `dW = Fnet * `ds, but if you try this you come up with only half of the answer.

In the book it shows that F = kx, and taking the antiderivative ==> `dW = (antiderivative from x2 to x1)F`dx = (antiderivative from x2 to x1)kx`dx = 1/2 kX^2. If I use `dW = 1/2 kX^2, I am able to arrive at the right answer. What is the difference between `ds and `dx? Between X and `ds? Why do I need to integrate for this one and not others? Thank you for your help.

RESPONSE FROM INSTRUCTOR:  `dW = Fnet `ds applies to a constant force parallel to the direction of the displacement `ds.

If you have a variable force, as we have done for springs you have to multiply average force by displacement.

The average of a function over an interval is equal to the integral over that interval, divided by the length of the interval.

Since Fave = integral / interval we have Fave * interval = integral. Thus `dW = Fave * interval = integral.

`ds stands for displacement. The displacement from x = 0 to x = X is (X - 0) = X.

You integrate because the force isn't constant; as indicated above integration effectively allows you to get the average value of the force.

You could similarly integrate the approximate cubic force function for a rubber band to get the work required to stretch from one length to another.