Notes from Class 1106

Physics I Quiz 1106

The tables below summarize the situation analyzed during the preceding class.  The first table uses linear approximations over 2000-km intervals and the second uses exact values, obtained from calculus.

The first table tells us that the approximate PE per kg at 'altitude' 10,000 km is 39,185,541 Joules / kg, which we round off to 39,200,000 J / kg.  This information is included in the figure below.

If we multiply this result by 75 kg we obtain the PE of the 75-kg object, which will be about 3,000,000,000 Joules.

The first table tells us that the approximate PE per kg in a circular orbit at 'altitude' 10,000 km is about 12,200,000 J / kg.  This information is also included in the figure below.

If we multiply this result by 75 kg we obtain the KE of the 75-kg object, which will be about 915,000,000 Joules.

The table tells us in a similar fashion that the PE and KE per kg at 'altitude' 8000 km are respectively about 35,800,000 J / kg and 14,000,000 J / kg, respectively, as indicated in the table below.

For a 75 kg object we obtain PE and KE of about 2,700,000,000 J and 1,050,000,000 J.

 

We note that the PE decreases and the KE increases.  The changes per kg are about -3,400,000 J / kg for PE / m and +1,700,000 J / kg for KE / m.

This amounts to a total of -1,700,000,000 J / kg.  For a 75 kg object this would be a change of -1,275,000,000 J.

Note that | `dKE | is about half of | `dPE |.  It turns out that for circular orbits the ratio is exactly half. 

The pilot would have to find a way to 'fall' 2000 km while speeding up from about 4950 m/s to about 5300 m/s.  It's easy to speed up while falling but this 'fall' would decrease PE / m by 3,400,000 J / kg while the desired increase in KE / m is only 1,700,000 J / kg.  In the absence of nonconservative forces we would have `dKE = - `dPE, but here `dKE has only half the magnitude of `dPE.  So some nonconservative force would have to be applied.  Since `dKE + `dPE, per kg, is +1,700,000,000 J and `dPE, per kg, is -3,400,000,000 J we see that `dKE + `dPE < 0.

General conservation of energy tells us that `dKE + `dPE + `dWnoncons = 0, and since `dKE + `dPE < 0 it follows that `dWnoncons > 0.  That is, the spacecraft would have to do positive work against nonconservative forces.

This could be accomplished by a 'backward' engine burn--i.e., turn the spacecraft so that its engines are pointing in the direction of motion and fire them.  The engines exert a force in the 'backward' direction against the ejected gases; however the 'backward' direction is the direction of motion so the spacecraft exerts a force in the direction of motion, doing positive work against the escaping particles.  The result is a decrease in KE, which seems counterproductive since we wish to gain KE and lose PE.  

However the loss of KE changes the orbit from circular to elliptical.  The new elliptical orbit takes the spacecraft 'down' toward its lower orbit, and as it 'falls' it speeds up.

Another 'burn' would be necessary as the craft approaches the lower altitude in order to reorient the orbit to a circular pattern.  We won't go into detail here about this second 'burn', except to note that orbital mechanics are quite complex.  You don't just aim the Space Shuttle 'up' at the Space Station and drive on in.  You gotta be pretty good to pilot one of those things.

Note that the tables below could be extended.   If we extend the second table, which gives us the accurate as opposed to approximated values of PE / m (note that our calculations of KE / m did not involve approximations and are already accurate) we find that PE / m grows more and more slowly.  Looking at the table we find that PE / m grows from almost 40,000,000 J / kg at 'altitude' 10,000 km to 60,000,000 J / kg before we reach  'altitude' 160,000 km and to 61,000,000 J/kg by the time we reach 'altitude' 230,000 km.  However to reach 62,000,000 J / kg 'altitude' has to increase to over 550,000 km, and an increase in 'altitude' to 1,000,000 km results in PE/m equal only to about 62,300,000 J / kg.  At 'altitude' 4 million km we get PE/m = 62,619,406.58 J/kg, relative to surface.

It appears that PE / m is leveling off, and it appears conceivable that PE / m could approach a finite limiting value (in somewhat the same way that I can move toward a wall by moving half of the distance, then half the remaining distance, then half the remaining distance, etc.--always approaching the wall, and eventually approaching it as closely as you might wish no matter how close you wish, but never actually reaching it), and this limiting value is around probably less than 63,000,000 J / kg.

This means, among other things, that if you give an object of mass 1 kg an initial KE in excess of of 63,000,000 J and the only force it encounters is that of the gravitational field of the Earth, it will keep going forever and never 'fall back'.  We have essentially done this with the Voyager spacecraft launched well over 30 years ago, and now beyond the solar system.  It will keep going until it finally runs into something, and out where it is there's not much for it to run into.  Actually it will eventually be 'captured' in the orbit of some star, the orbit will decay, and probably after a very long time (billions of years) it will fall into that star.

The function that gives the potential energy, relative to infinity, of an object in orbit around the Earth is -G M m / r , where G = 6.7 * 10^-11 N m^2/kg^2, M is the mass of Earth (approx. 6 * 10^24 kg), m the mass of the satellite and r the radius of the orbit.  

The calculation is straightforward.  In the figure below we rearrange PE = - G M m / r to get PE / m = - G M / r, the PE per unit of mass (e.g., PE / kg as in the tables).  Substituting the radius and mass of the Earth we get PE / m = -62,500,000 J / kg.

Note that in the figure below the - sign got erroneously left off in the last two steps.

Had we used the more accurate mass 5.97 * 10^24 kg this result would have had a slightly greater magnitude.

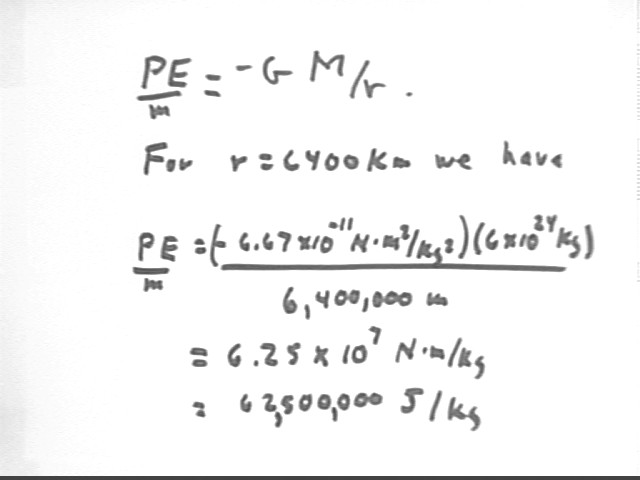
At 'altitude' 10,000 km we have PE / m = 40 MJ (megaJoules) relative to the surface of the Earth.  As we approach infinite distance our spreadsheet tells us that PE / m approaches a limit of around +63 MJ relative to the surface of the Earth.

Relative to infinite distance our equation PE / m = - G M / r, easily derivable by students familiar with calculus, tells us that the PE / m at the surface of the Earth is about -63 MJ.

These results are consistent.  The first result tells us that we need +63 MJ / kg to 'escape' to inifinite distance, which means PE / m change from here to infinity is +63 MJ / kg.  The second result tells us that between infinity and here the PE / m change is -63 MJ / kg.  This is consistent with what we understand about PE--going one way it goes up, coming back the other way it goes down.

 

Plugging in the mass of the Earth, G and the orbital radii 6400 km + 10000 km = 16,400,000 m and 6400 km + 8000 km = 14,400,000 m we get respective PE / m values about -24,400,000 J / kg and -27,800,000 J / kg.

From the 10,000 km to 8,000 km 'altitudes' the PE / m changes from -24,400,000 J / kg to -27,800,000 J / kg, which is a change of PEf - PE0 = -27,800,000 J / kg - (-24,400,000 J/kg) = -3,400,000 J / kg.

We have already used the tables to find the change, which according to the second (more accurate) table is -3,400,000 J / kg.

This illustrates the fact that PE change is the same no matter what you reference point (reference point surface of the Earth, or reference point infinite distance, it doesn't matter).

University Physics students only:

The force exerted by gravity on a given mass by the Earth is of the form F(r) = k / r^2, where k is a constant.  What is the simplest antiderivative of this function?  What do we get when we integrate F(r) = k / r^2 from r = 6,400,000 to r = 16,400,000?

The simplest antiderivative of k / r^2 with respect to is variable, which is r, will be - k / r.  We easily see this by expressing k / r^2 as the power function k r^-2 and using the fact that the derivative with respect to r of r^n is  n r^(n-1).

If k / r^2 is integrated from 6,400,000 to 16,400,000 the result is the change in the antiderivative function:  

-k / 16,400,000 - (-k / 6,400,000) = .0000000953 k, approx.

What is the force exerted by Earth's gravitational field on a 75-kg mass at the surface of the Earth?  What therefore is the value of k, including units, for a 75-kg mass?  Use the resulting function to determine exactly how much work is required against gravity as we raise a 75-kg mass from the surface of the Earth, at r = 6,400,000 m, to 'altitude' 16,400,000 m. 

We know that when r = 6,400,000 meters we have F = 75 kg * 9.8 m/s^2 = 735 N.  So if F = k / r^2 we have k = F * r^2 = 735 N * (6,400,000 m)^2 = 3.01 * 10^10 N m^2.

Thus for the 75 kg mass we have F = ( 3.01 * 10^10 N/m^2) / r^2.

To find the work required to raise the mass we integrate force * distance -- i.e., we integrate F with respect to r.

Our antiderivative is -( 3.01 * 10^10 N/m^2) / r.

Between r = 6,400,000 m and r = 16,400,000 m the antiderivative changes by 

-( 3.01 * 10^10 N/m^2) / (16,400,000 m) - (-3.01 * 10^10 N /m^2) / (6,400,000 m) 

= 2,900,000,000 J, approx.. 

This is the increase in our PE from surface to 'altitude' 10,000 m.

Comparing the result from the second table's PE / m change of 38,200,000 J / kg we multiply by the 75 kg to get a PE increase of 75 kg * 38,200,000 J / kg = 2,900,000,000 J, in agreement with the result we obtained from the integration.

PE calculated by Trapezoidal Approximations of Orbital Energies per Kg, based on 2000-km intervals.

KE per kg calculated accurately (within roundoff error) from orbital velocity.
altitude y, km g in m/s^2 ave g for interval `dW / m in J per kg orbital vel m/s orbital KE / m in J per kg  PE / m relative to surface, J per kg KE / m change from next-lower orbit, J per kg PE / m change from next-lower orbit, J per kg ratio of KE change to PE change
0 9.8
2000 5.688889 7.744444 15488889 6912.79 23893333 15488889
4000 3.711243 4.700066 9400131 6212.642 19298462 24889020 -4594872 9400131 -0.48881
6000 2.610614 3.160928 6321857 5689.606 16185806 31210877 -3112655 6321857 -0.49236
8000 1.935802 2.273208 4546416 5279.731 13937778 35757293 -2248029 4546416 -0.49446
10000 1.492445 1.714124 3428247 4947.332 12238049 39185541 -1699729 3428247 -0.4958

 

Exact Calculations of Orbital Energies per Kg (PE from integral of force function, KE from orbital velocities, all accurate to 2 significant figures)

 
altitude y, km `dW / m in J per kg orbital vel m/s orbital KE / m in J per kg PE / m relative to surface, J per kg KE / m  change from next-lower orbit, J per kg PE / m change from next-lower orbit, J per kg ratio of KE change to PE change  
0
2000 14933333 6912.79 23893333 14933333
4000 9189744 6212.642 19298462 24123077 -4594872 9189744 -0.5
6000 6225310 5689.606 16185806 30348387 -3112655 6225310 -0.5
8000 4496057 5279.731 13937778 34844444 -2248029 4496057 -0.5
10000 3399458 4947.332 12238049 38243902 -1699729 3399458 -0.5

Overview of Gravitation

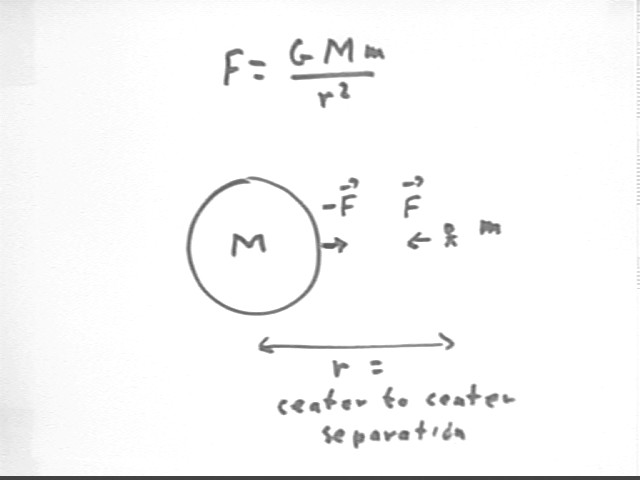
Newton's Law of Universal Gravitation is expressed as in the figure below.  Two masses whose centers are separated by distance r exert a mutual attractive force on one another, with F = G M m / r^2.

We can model this law with a 'flux model'.  By analogy with a light source, in which the power of the emitted light is spread over spheres of greater and greater radius as we move further and further from the source, we think of a mass giving rise to a gravitational flux.  Mass M will result in a total flux of 4 pi G M.

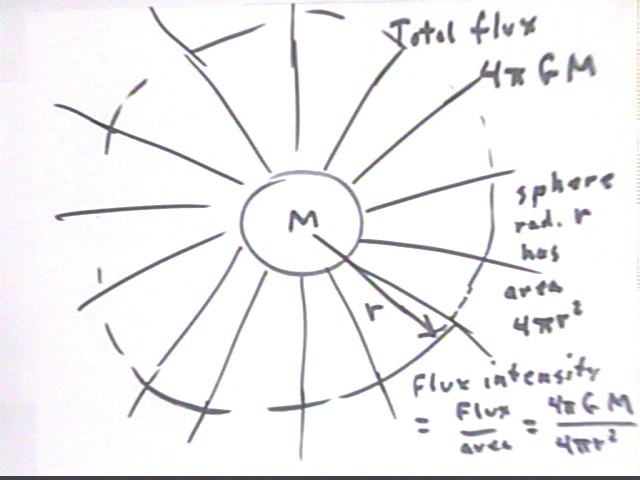
At distance r from the center of the mass this flux will be spread over a sphere of radius r, giving an average flux density

If the mass is spherically symmetric the flux will be spread uniformly over the sphere and will hence give a uniform flux density.

This flux density is the strength of the gravitational field.  For a spherically symmetric object the flux density at a given distance is a constant G M / r^2.

Flux density is interpreted as gravitational field strength.  It has units of N / kg or equivalently m / s^2.  This flux density can be interpreted as either force / unit of mass or as the acceleration of gravity, one being equivalent to the other.

From the fact that the acceleration of gravity is g = G M / r^2, we find that the gravitational force on an object is F = m g = m ( G M / r^2) = G M m / r^2, which is Newton's Law of Universal Gravitation.

The flux model reinforces the inverse-square nature of the law by invoking a picture of gravitational influence being spread over concentric spheres, whose area increases as r^2 with the result that flux density is proportional to 1 / r^2.

The idea of flux will be important when we study another inverse-square law, Coulomb's Law, and its ramifications.