Notes from Class 1108

Physics I Activity 1108

Angular Positions in Radians:

Sketch a circle with an x-y coordinate system centered at the origin.

The angular position of a point on a circle is measured in radians, starting from the positive x axis and moving counterclockwise.

There are about 6 radians around the circle.  Based on the assumption that there are indeed 6 radians around the circle sketch the positions on the circle that correspond to 0, 1, 2, 3, 4, 5, and 6 radians.

There are actually 2 pi or about 6.28 radians around the circle.  Modify your sketch to more accurately indicate the positions that correspond to 0, 1, 2, 3, 4, 5, and 6 radians.

Indicate the point which lies at angular position 2 radians and at a distance of 1.2 times the radius of your circle.

A right angle is pi/2 or about 1.57 radians.  A circle is perpendicular to a radial line (a line from the center to the circle).  Suppose your circle represents the Earth.  If you want to start a circular orbit whose radius is 1.2 Earth radii, beginning at the 2 radian position, then in what direction do you have to start out?

If you know your angular position then how do you determine the initial direction required for a circular orbit?

If you want to 'shoot' a projectile straight 'up', which means straight away from the center of the circle, starting from the 1 radian position, then in what direction (in radians) should you 'shoot' it?

See Notes on Initial Questions at the end of this page.

Using the program

Go to webpage at 164.106.222.236.  Click on Physics I and proceed until you get a line of blue 'buttons' across the top of your screen.  Click on the one that says 'simulations'.

Click on GrvField and choose to run the thing.

To start with you will determine the velocity required for a circular orbit at a distance of 1.2 Earth radii. 

Give the following answers to the prompts:

See if you've achieved a segment of a circular orbit.  If not go back and make the appropriate changes to the quantities you've entered until you have.  Keep notes on the quantities you've entered and the results of your work.  If your screen gets too messy enter 999 or 9999 at the appropriate point and clear it.

Then increase the duration of the simulation until you've got a full circle.  If the circle doesn't come back to its starting point it's not a circle.  Continue until you've got a circle.  See what the required velocity is.

Now find the velocity with which a projectile would have to be 'shot' from the surface of the Earth, ignoring air resistance, to get 'up' to the altitude of the orbit you have just created. 

Repeat but change your initial angular position to 1 radian (and of course change the initial direction of the 'shot' accordingly), and adjust your velocity to get closer to your goal.  Adjust the time of the simulation to allow the projectile to stop moving outward and begin falling back. Continue changing the intial angular position and your angular velocity until you manage to just reach the circular orbit you created in the first part of the experiment.

Repeat this procedure for the orbital radius you have been specifically assigned.

That is, determine the velocity necessary to maintain that orbit and the velocity required to achieve the altitude of that orbit.

Now achieve an elliptical orbit that just skims the surface of the Earth.

Starting from a position at 2 Earth radii from the center, adjust your initial velocity until you have an orbit that just touches the Earth's surface.  Observe everything you can about the motion of the satellite in this orbit.

Analysis

For each radius you investigated determine, by setting centripetal acceleration equal to gravitational acceleration, the 'actual' velocity for that circular orbit.

Compare with the velocities you obtained.

According to your observations:

According to theory:

For the elliptical orbit, based on your observations:

For the elliptical orbit, based on theory:

Speculate on what sorts of strategies are required to get a Space Shuttle into a circular orbit at an 'altitude' of 400 km.  Keep in mind that rocket fuel doesn't carry enough energy to even get its own mass into orbit.

Speculate on what strategies are required to get a spacecraft to the Moon, which is about 60 Earth radii away, and back.

Notes on Initial Questions:

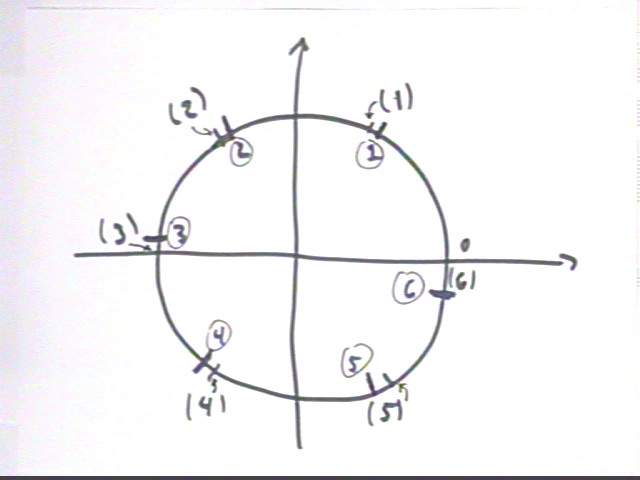
The circumference of a rough circle is first divided into 6 equal arcs between approximate angles 0, 1, 2, 3, 4, 5 and 6 radians.  The corresponding positions are indicated by the numbers in parentheses. 

Then the positions are adjusted for the fact that there are 2 pi rad = 6.28 rad, approx., around the arc.  This places the 6 radian position about .28 radians 'short' of the complete arc, at the position marked with the circled 6.  The other 'adjusted' positions are also indicated by circled numbers.

This figure is not drawn with great accuracy.  You should see if you can improve on it.

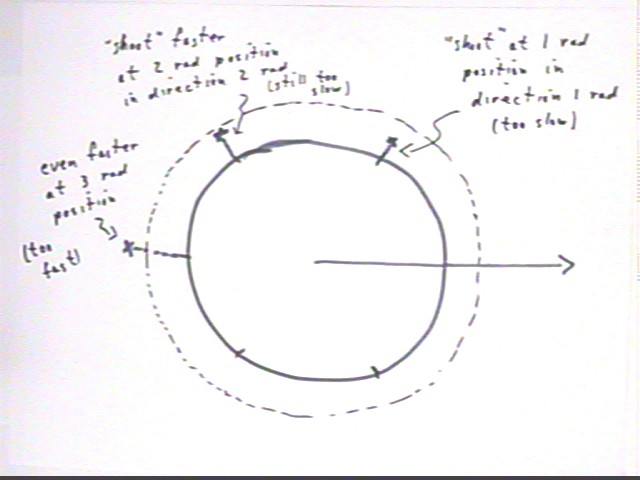
The figure below indicates the Earth with a tall tower from which a series of projectiles are 'shot'.  Throughout this exercise we are ignoring air resistance. 

The first projectile falls in an approximately parabolic arc to Earth and lands at the position indicated by the numeral 1.  The second also falls to Earth but lands at position 2, and the third falls to Earth landing at position 3.  The fourth is 'shot' at just the right velocity, always curving toward Earth but never reaching it, but never moving away either, remaining in a circular path.

Which of the first 3 velocities is the slowest, which is the fastest, and to achieve circular orbit would it be necessary to use a greater or a lesser velocity than the velocity of projectile 3?

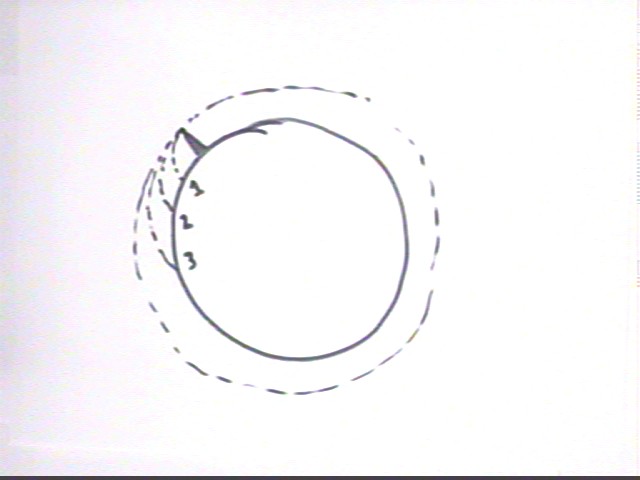
To achieve a circular orbit at, for example, the 2.4 radian position we must at this position have just the right velocity and by the basic geometry of circles the direction must be perpendicular to a radial line (i.e., a line from the center to the point).  A right angle is 1.57 radians so the initial velocity must be at angle 2.4 rad + 1.57 rad = 3.97 rad.   This would result in an orbit in the counterclockwise direction around the planet.

Note that we could also have an initial velocity in the opposite direction, at 2.4 rad - 1.57 rad = 1.83 rad.  This would cause an orbit in the clockwise direction.

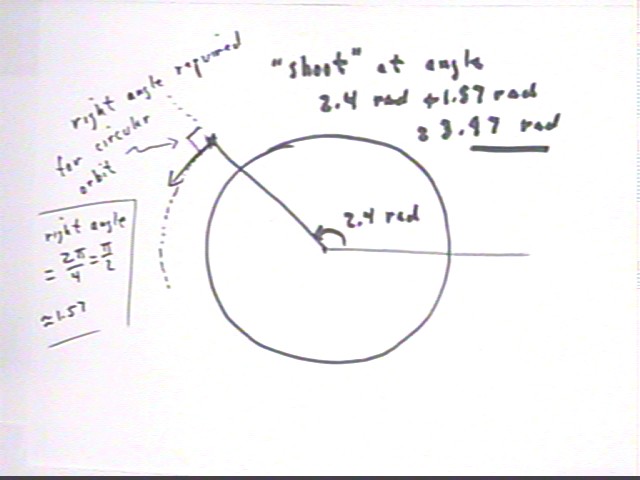
To reach a given orbital 'altitude' from the surface of the Earth with no leftover KE we must 'shoot' directly outward.  This means that our initial velocity is in a direction leading straight away from the center of the Earth.  The velocity is therefore along a radial line and the direction of the initial velocity must be the same as our angular position.  So if we are at position 1 radian we have to have an initial velocity in the 1 radian direction.  Similarly at 2 and 3 radian position initial velocities must be in the 2 radian and 3 radian directions, respectively.

The figure below shows trial-and-error attempts to reach the altitude of the indicated circular orbit.  The first attempt at 1 radians fell short; we conclude that our initial velocity was too low.  The second attempt, at 2 radians, uses a higher initial velocity but doesn't quite make it.  The third attempt, at 3 radians, 'overshoots' the desired orbit, from which we conclude that our initial velocity was too high.

It is clear that we could continue refining our attempts until we actually 'rise' to precisely the right 'altitude'.  We can use any sequence of angular positions we wish.