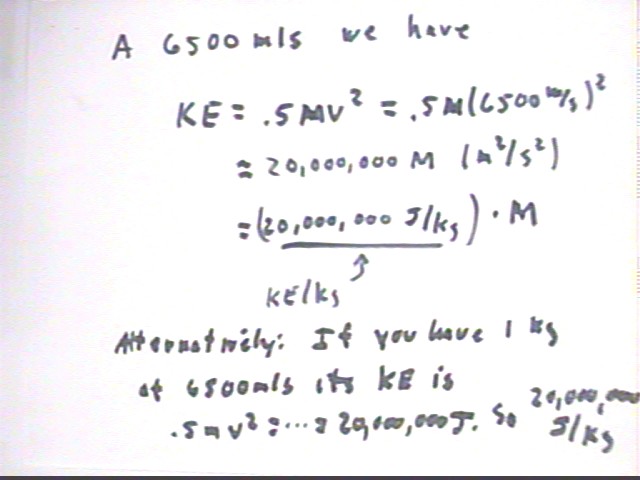
Physics I Quiz 1113
From the demonstration given at the beginning of class you should have noted the following:.
At 6500 m/s we achieved a nearly circular orbit at r = 1.5 Earth radii. We required an initial velocity of about 6000 m/s to raise a projectile from the surface of the Earth to a position of rest at r = 1.5 Earth radii.
Answer the following questions:
Using the quantities observed what are the KE / kg and the PE / kg for the circular orbit whose radius is 1.5 * Earth radius?
A 1 kg mass moving at 6500 m/s has KE = .5 * 1 kg * (6500 m/s)^2 = 20,000,000 Joules, approx., so
KE / m = 20,000,000 J / (1 kg) = 20,000,000 J/kg.
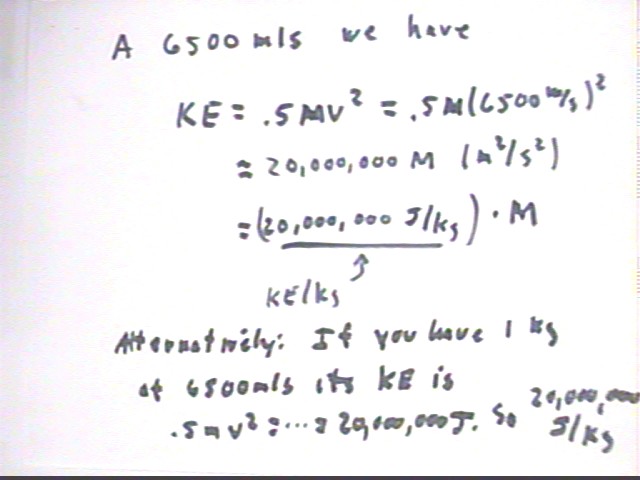
The is no PE change in the orbit, since there is no displacement in the direction of the gravitational force. The only PE change takes place in the projectile which is raised from the surface to the position of the orbit. So we analyze this situation.
There is by assumption, not in fact, no nonconservative force (e.g., no air resistance) acting on the mass as it 'coasts' up to the position of the orbit. Thus the work-energy theorem tells us that for this process `dPE + `dKE = 0. Since we know initial velocity (6000 m/s) and final velocity (at rest, vf = 0) we easily calculate the change in KE of a 1 kg mass:
`dKE = KEf - KE0 = 0 - .5 * 1 kg * (6000 m/s)^2 = -18,000,000 Joules,
which tells us that `dPE = -`dKE = +18,000,000 J, so that relative to the surface we have
PE / kg = 18,000,000 J / (1 kg) = 18,000,000 J / kg

What happens to the orbit if the projectile is started off at .1 radian (about 6 degrees) above, and then at the same angle below, a direction which is perpendicular to the radial direction? How does the motion of the projectile in this case illustrate conservation of energy?
Suppose we wish to construct a circular orbit of radius 1.7 Earth radii starting at angular position 5 radians. Sketch this situation and specify the initial angular position, initial radius and the direction of the initial velocity. Also show the path of the projectile if we give it an initial velocity which is too low, and also if the initial velocity is too high.
The radial line to this position makes angle 5 rad with the direction of the positive x axis and has length 1.7 rEarth, as indicated in the figure. The initial velocity must be perpendicular to the radian line and must therefore make angle 5 rad + 1.57 rad or 5 rad - 1.57 rad with the direction of the positive x axis. Calculating these angles:

Is it possible to start off with a velocity which is 'too low' and have the resulting orbit 'miss' the Earth? Explain.
Is it possible to start off with a velocity which is 'too high' for a circular orbit and not end up forever 'lost in space'? Explain.
A torque of .43 m * N is exerted on a meter stick whose moment of inertia is .01 kg m^2. Remember that Newton's Second Law F = m a is translated into angular terms by replacing F with torque and m with moment of inertia. What will be the angular acceleration of the meter stick? How long will it take the meter stick to accelerate to 10 rad / sec and through what angle will it move in the process?
We know that Newton's Second Law for rotation is torque = moment of inertia * angular acceleration, represented tau = I * alpha. To find angular acceleration from the given information we therefore find
angular acceleration = alpha = tau / I = .43 m N / (.01 kg m^2) = 43 rad/s^2.
The units of the calculation are as follows:
To attain 10 rad/sec at

Each centimeter of the meter stick in the preceding problem, which is being rotated about its center, has mass 1.2 grams. At 10 rad / sec how fast is the cm furthest from the axis of rotation moving and what is its KE? Answer the same question for a point halfway from the axis of rotation to the end.
Experiment:
You have been provided with a 'stick' and a marker top on which to rotate the stick. Balance the stick on the marker top.
Give the stick a good nudge and try to get it to rotate as many times as possible about a vertical axis thru the center of the marker top.
Take the data you will need to determine the angular acceleration of the stick as it coasts to rest, assuming uniform angular acceleration.
Find the angular acceleration of the stick.
Using the information below find the initial angular kinetic energy of the stick.
Using the dimensions of the stick determine its volume, then using its density determine its mass. Then using the formula given determine its moment of inertia.
Use the formula for KE and quantities you found in your previous analysis to determine the stick's initial KE.
