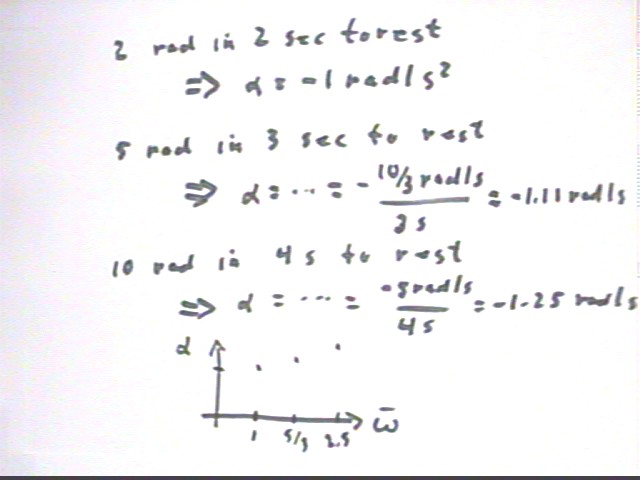
Physics I Quiz 1117
A 'stick' rotates repeatedly from different initial velocities to rest, rotating through 2 radians in 2 seconds, then through 5 radians in 3 seconds, then through 10 radians in 4 seconds. How well do these data support the contention that the angular acceleration of the system is independent of velocity?
The calculation of the angular accelerations is straightforward by analogy with calculations we would make for linear motion with v0, vf, vAve, `ds, a, etc..
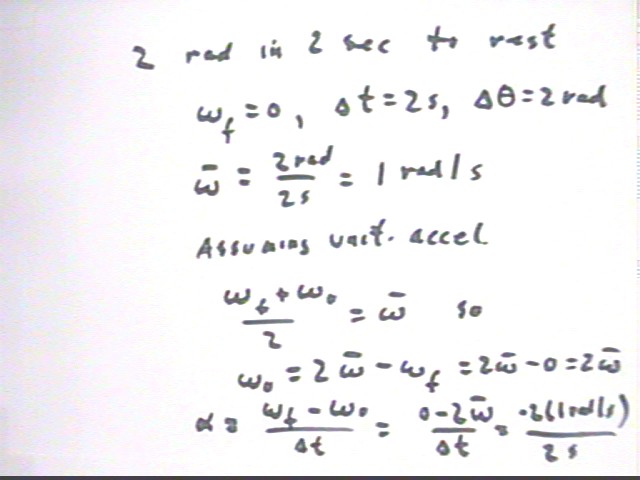
We obtain the graph of angular accel alpha vs. ave angular velocity omegaAve depicted in the figure below.
The graph appears to be increasing, but the differences in alpha values are not great and could be just a coincidental result of experimental uncertainties.
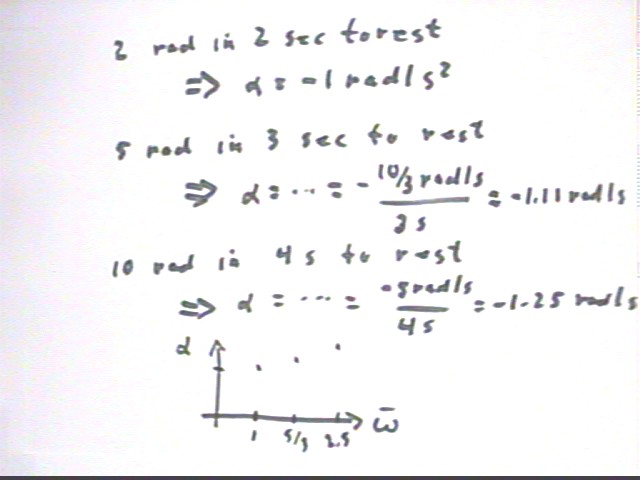
We note that angular accelerations were calculated using the assumption that angular accel in each instance would be uniform. If we find from our experiment that this assumption results in the conclusion that angular accel does depend on angular velocity, we are left with the conclusion that angular acceleration is not uniform. Thus we contradict our original assumption, telling us that angular accel is not uniform but making our conclusions about just how angular accel depends on angular velocity invalid. Our conclusion contradicts our hypothesis that angular accel is independent of angular velocity; but we used our hypothesis in our analysis. This leads to an interesting logical situation.
It the 'stick' in the preceding has mass 200 grams and length 30 cm then its moment of inertia is 1/12 M L^2 = .0015 kg m^2. If masses of 50 grams are added at the ends of the 'stick' then what will be the new moment of inertia of the system? What is the ratio of moments of inertia before and after adding the masses?
We easily verify that 1 / 12 M L^2 gives us I = .0015 kg.
Having added the two 50 g masses the mass of the stick is now 300 g, which is 300 / 200 = 1.5 times the original mass of the stick alone. So the mass ratio is 1.5.
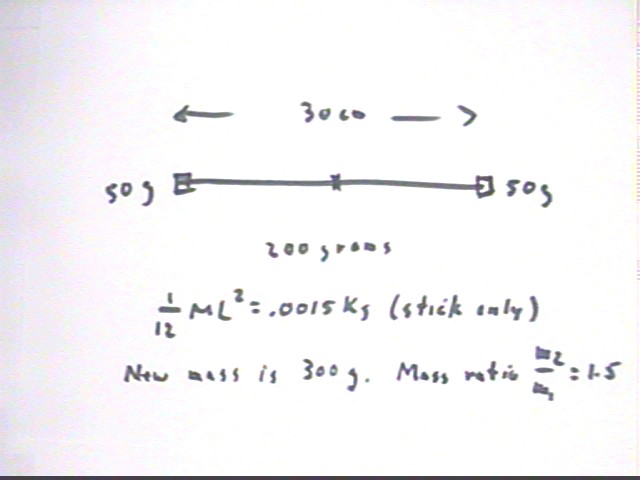
Each mass added moment of inertia m r^2 = .05 kg (.15 m)^2 = .001125 kg m^2 to the system, giving us a total moment of inertia of .00375 kg m^2.
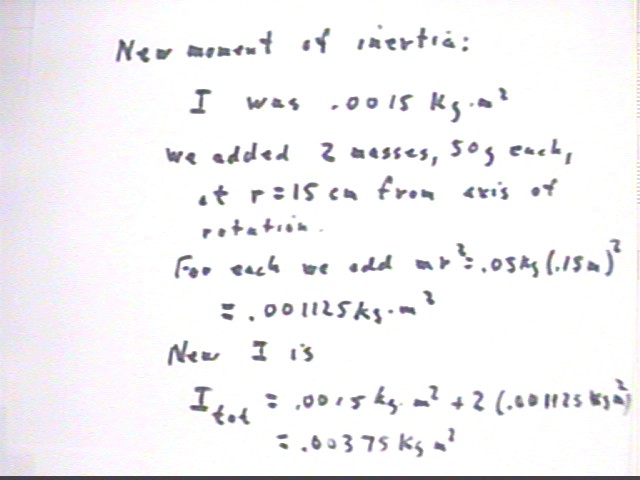
The ratio of moments of inertia is easily seen to be 2.5.
The torque that accelerates the system comes from friction, which is proportional to the weight of the system. What is the ratio of the torques of the system? Using the ratio of the torques and the ratio of the moments of inertia, what should be the ratio of the angular accelerations of the two systems?
Since the torque is the result of frictional forces between the system and is support, and since the frictional force is proportional to the weight and hence the mass of the system, the ratio of torques will be equal to the ratio 1.5 of masses.
So we have a system with 2.5 times the moment of inertia, being accelerated with 1.5 times the torque. The ratio of angular accelerations will therefore be 1.5 / 2.5 = .6. I.e., the increased torque would tend to increase the magnitude of the acceleration but the increased moment of inertia would tend to decrease acceleration, and since moment of inertia increases more than torque the magnitude of the acceleration is less.
This matches our first visual observations of the system after the 'blocks' were added. It seemed to 'coast' a lot more easily than the original system, indicating an angular acceleration of less magnitude than before (the thing slowed down faster than before).

What is the approximate average torque exerted by friction on the original system?
What should be the approximate average torque exerted by friction on the second system?
What should be the approximate average acceleration of the second system?
The original acceleration calculated for the data of the quiz had an approximate average angular acceleration of -1.1 rad/s^s. It follows that the angular acceleration after the addition of the 50-g masses will be .6 as much, or .6 * (-1.1 rad/s^2) = -.66 rad/s^2.
The original torque would be
tau = I * alpha = .0015 kg m^2 * (-1.1 rad/s^2) = -.00165 m N.
The second system would experience 1.5 times the frictional force and therefore 1.5 times the torque, or -.00165 m N * 1.5 = -.0025 m N. We could calculate the resulting angular acceleration, obtaining
alpha2 = -.0025 m N / (.00375 kg m^2) = -.66 rad/s^2, in agreement with the result obtained from ratio reasoning.

How can we calculate the approximate moment of inertia of a 30 cm stick with total mass 200 g, rotated about an axis thru its center?
To calculate the moment of inertia of a uniform stick we must add up all the m r^2 contributions for the entire stick. We can't actually do this, except using calculus, but we can obtain a good approximation.
Consider the 1-cm length of the stick in the neighborhood of x = 7 cm from the axis of rotation, as indicated below. We easily calculate that the mass per cm. is about 6.67 g / cm, so this 1-cm length will have mass .667 g. We easily find that the moment of inertia of this 1-cm segment is `dI = m r^x = m x^2 = 6.67 g * (7 cm)^2 = 327 g cm^2.
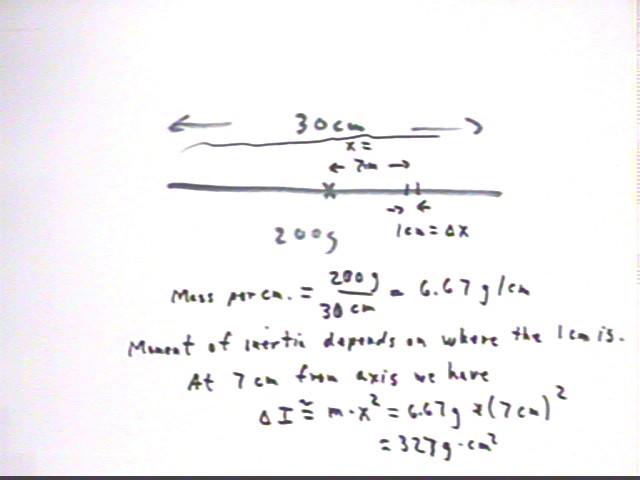
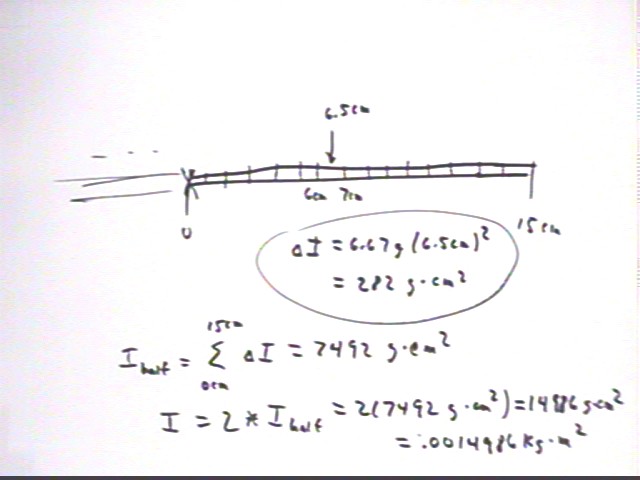
We can easily set up the calculation we need to estimate the total moment of inertia of the stick. We first note that the 7th 1-cm length along the stick runs from x = 6 cm to x = 7 cm, and use its average distance from the center as 6.5 cm as a basis for calculating its moment of inertia (this will not give us a completely accurate result because the r^2 factor is not linear so the 'midpoint' as far as r^2 is concerned is at a different point, but for 1-cm intervals on a 30-cm stick the difference will be fairly small).
We obtain `dI = 282 g cm^2.
We can easily set up a spreadsheet to calculate and sum the same result for the midpoints of all 15 1-cm intervals to the right of the axis of rotation. We obtain
Ihalf = sum(`dI) = 7492 g cm^2.
The other half of the stick will have identical moment of inertia, being completely symmetric with respect to the axis of rotation with the half we just analyzed, so we get
I = 2 * Ihalf = 14984 g cm^2 = .001498 kg m^2,
very close to the value .0015 kg m^2 obtained for 1/12 M L^2.
University Physics: A uniform stick 30 cm long has mass 200 grams, as in the above. Answer the following:
We will get
The moment of inertia per cm is 6.67 g * x^2. A graph of 6.67 x^2 vs. x is depicted below.
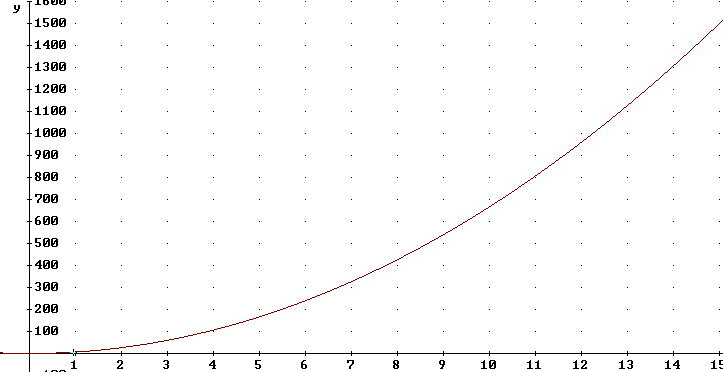
To get moment of inertia we multiply average moment of inertia per cm by the number of cm. For any small interval `dx between x = 0 and x = 15 cm we can therefore approximate the contribution of that interval to the total moment of inertia by finding the area of the corresponding trapezoid, whose altitude closely approximates the moment of inertia per cm at that position and whose width is the number of cm in the segment.
This means that the moment of inertia is the area beneath the curve and we can find the moment of inertia by integrating the function over the interval.
We could also have concluded that since total moment of inertia is the ave moment of inertia per cm * number of cm the total moment of inertia is the integral of this moment of inertia per cm function.
A Riemann Sum is also useful in understanding why we integrate the function we do. The Riemann Sum for this function would be a sum of terms m x^2 = (6.67 `dx) * x^2, leading to the integrand 6.67 x^2 dx.
Integrating 6.67 x^2, or more precisely 20/3 x^2, with respect to x from x = 0 to x = 15 we first get antiderivative 20/9 x^3 (our 'change-in-moment-of-inertia' function), which between x = 0 and x = 15 changes by
I = 20/9 ( 15^3 - 0^3) = 7500,
representing the 7500 g cm^2 contribution of the 'right-hand' half of the stick. Adding the equal contribution of the 'left-hand' half we get total moment of inertia I = 15,000 g cm^2 = .0015 kg m^2.
What is the moment of inertia of the styrofoam disk displayed in class, with sixteen 9.4 gram bolts located near the rim at 12 cm from the center?
The mr^2 for each bolt is 9.4 g * (12 cm)^2 = 1354 g cm^2, so the total mr^2 will be 16 times this or
The mass of the Styrofoam is fairly small and doesn't contribute a great deal to the total moment of inertia, though it isn't completely insignificant.
