Notes from Class 1120

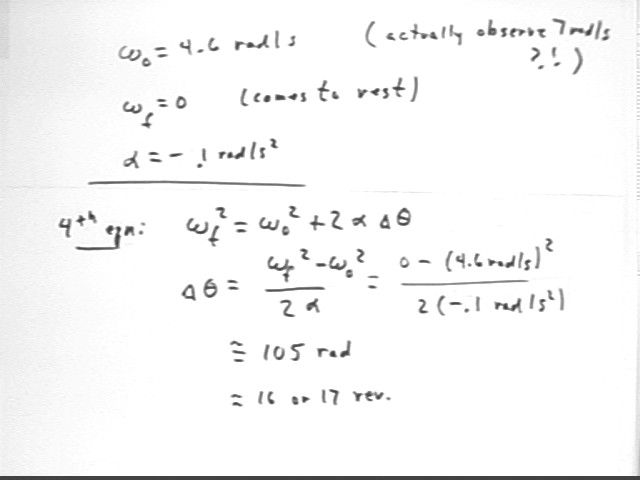
Physics I Quiz 1120

The bolts attached to the 'wheel' demonstrated in the 11/18 class have moment of inertia approximately .0022 kg m^2, calculated about an axis thru the center of the bearing which supports the disk.  The moment of inertia of the Styrofoam disk itself is about .0002 kg m^2.

If this disk was rotating at 2.4 revolutions / second what would be its total kinetic energy?

KE = .5 I omega^2.  

I = .0024 kg m^2 (sum of mr^2 for bolts + sum of mr^2 for foam is total mr^2)

omega = 2.4 rev / sec = 2.4 * 2 pi rad / sec = 15 rad/sec.

So KE = .5 * .0024 kg m^2 * (15 rad/sec)^2 = .273 J.

If a 20-gram is attached to the rim of the wheel, with the weight just past the 'top' of the wheel, and if the wheel is allowed to rotate while the weight 'falls' to a point at the same altitude as the axis of rotation, then how what should be the KE of the wheel at this point?  What therefore is the velocity of the wheel, whose diameter is 13 cm?

The 20 gram mass loses PE.  The rest of the wheel doesn't lose PE (parts do lose PE but other parts gain PE--for any part that goes down another part goes up).  So the net change in PE is the change in the PE of the 20 gram mass.

Thus `dPE = work done against gravity = -work done by gravity = - weight * vertical displacement = - (.020 kg * 9.8 m/s^2) * (.13 m) = -.0255 J.

There's not much friction so `dWnoncons = 0, approx..

So `dKE + `dPE = 0 and `dKE = - `dPE = -(-.0255 J) = .0255 J.

Since initial KE is 0 we therefore have

.5 I omega^2 = .0255 J so that

omega = +-sqrt( 2 * KE / I ) = +-sqrt( 2 * .0255 J / ( .0024 kg m^2) ) = +-4.6 rad / sec.

Note that when observed the system, coasting through at least a few revolutions after the weight fell off, exhibited an average angular velocity in excess of 1 rev / s, over 6.28 rad/s.  This should not happen if the moment of inertia of the bolts in the wheel was calculated correctly.  There is no way the the KE of the system can exceed the PE change of the falling mass.  The 20 gram mass was verified (hanging brass mass marked 20 g, confirmed by weighing).  The observed KE is about double the predicted KE.

Suppose that the weight slips off the wheel when its altitude is the same as that of the axis of rotation.  If the angular acceleration of the 'coasting' wheel is a uniform -.01  rad / s^2 then how long should it take the wheel to come to rest and through how many revolutions will it travel before coming to rest?

We know initial angular velocity is omega0 = 4.6 rad/s, final angular velocity is omegaF = 0 and angular acceleration is -.1 rad/s^2.

Using the fourth equation of motion we find that `d`theta = 105 radians, about 16 or 17 revolutions.  In practice the thing gets about 25 revolutions.

The calculatoin is depicted in the figure below.

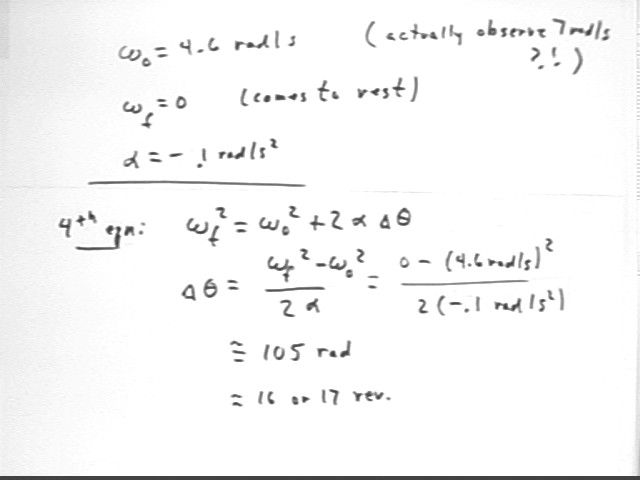
What is the net torque on the wheel and how much work is done by the net torque as the wheel comes to rest?

Newton's Second Law tells us the torque = moment of inertia * angular acceleration:

• tau = I * alpha

so we have

• torque = tau = I * alpha = .0024 kg m^2 * (-.1 rad/s^2) = -.00024 m N.

The work done by the torque is the product of torque with angular displacement:

• `dW = tau * `d`theta = 0.00024 m N * 105 rad = -.025 Joules, approx..  This should be the same as the PE loss of the 20 gram mass.  

The entire energy picture, from the initial state with the 20 g mass at rest 13 cm above the center altitude, is this:  

• PE is lost by the 20 gram mass, friction negative  work on the system so that the system does positive work against friction, KE = 0 at beginning and at end.  Thus `dPE + `dWnoncons = -.025 J + .025 J = 0, as must be the case.

What is the centripetal acceleration of the mass at the point where it is said to slip off?

aCent = v^2 / r .  v = r * omega.  So

• aCent = ( r * omega)^2 / r = r * omega^2 = .13 m * (4.6 rad/s)^2 = 2.7 m/s^2.

This is about .3 times the acceleration of gravity; the rubber band from which the weight hangs is supported by a steel paper clip and the coefficient of friction between the two is probably around this value.

We now pose the question in the figure below:  

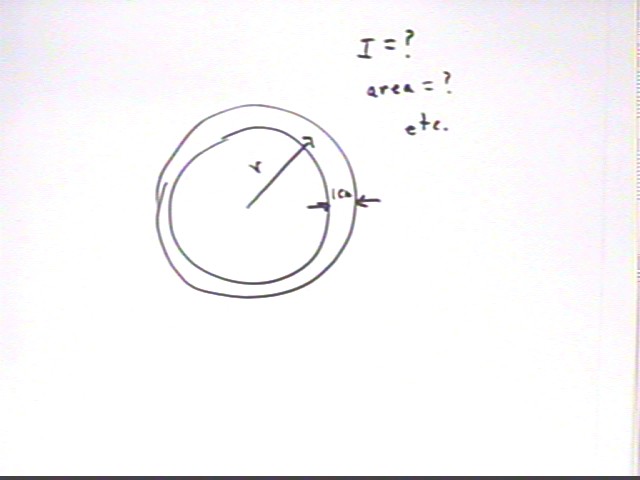
If we have a disk whose radius is 15 cm, with uniform mass distribution of 5 grams per cm^2 of surface area, what is its moment of inertia about an axis through its center and perpendicular to the plane of the disk?

• We begin by asking how much mass exists within a small range of distances from the center of the disk.  Use the range from 4 cm to 5 cm we see that the region that lies between 4 cm and 5 cm from the axis forms a ring whose area is pi * (5 cm)^2 - pi * (4 cm)^2 = 9 pi cm^2.  At 5 grams / cm^2 the mass of this ring is therefore 5 g / cm^2 * 9 pi cm^2 = 140 grams, approx..
• The moment of inertia of this ring is the sum of all m r^2 contributions from the ring.  Some parts of the ring are further and some are closer, but since the ring extends from r = 4 cm to r = 5 cm we use r = 4.5 cm as an approximate average, noting that r^2 isn't linear so that the average value of r^2 won't actually occur at this midpoint; however since the range from 4 cm to 5 cm is fairly small the actual average value of r^2 will occur reasonably close to the midpoint at 4.5 cm.
• With this assumption the moment of inertia will be simply m r^2 = 140 g * (4.5 cm)^2 = 2800 g cm^2, very approximately.

To get the total moment of inertia of the disk we could add up similar results from all the 1-cm ranges, from 0 cm - 1 cm up thru 14 cm - 15 cm, all calculated in the same way we just calculated the approximate moment of inertia of the disk from 4 cm - 5 cm. 

This process is easily set up on a spreadsheet.  We obtain the following results, where

• The first column consists of r values from 0 cm - 15 cm.  
• The second column contains the area of the circle corresponding to each r value.  
• The third column subtracts from the area of each circle the area of the preceding circle, giving us the area of the ring.  
• The fourth column gives the ring mass, obtained by multiplying the ring area by the area density 5 g / cm^2 to obtain mass in grams.  
• The fifth column contains the moment of inertia, obtained by multiplying the ring mass by the average of the radius and the preceding radius.

The total moment of inertia, in gram cm^2, is 35286 grams.  Converting this to kg m^2 we obtain about .035 kg m^2.  Note that this is about 10 times the moment of inertia of the disk used in the class demonstration.

Compare this with the 'ideal' moment of inertia for a disk, which is .5 M R^2.  The entire disk has radius R = 15 cm and mass M = 3.53 kg (total area pi * (15 cm)^2 = 706 cm^2, approx, multiplied by 5 g / cm^2).  Thus .5 M R^2 = .5 * 3.53 kg * (.15 m)^2 = .040 g cm^2.

University Physics only

The density of a sheet of Styrofoam, in grams / cm^2 of surface area, is .03.  A Styrofoam disk made from this sheet has radius 12 cm.  

• How much mass is there between r = 5 cm and r = 6 cm from the axis of rotation?  What is the approximate moment of inertia of this mass?

Using the procedure outlined above we find that the mass is (pi * (6 cm)^2 - pi * (5 cm)^2 ) * .03 g / cm^2 = 1 g, approx..  The moment of inertia, based on average r of about 5.5 cm, is thus m r^2 = 1 gram * (5.5 cm)^2 = 30 gram cm^2, approx..

• How much moment of inertia is there per cm of radius at the radial distance r = 9 cm?

The circumference of the r = 9 cm circle is 2 pi * 9 cm = 18 pi cm.  A ring with this circumference and a width of 1 cm would have area approximately equal to the area of a rectangle whose length is equal to the circumference and whose width is equal to the width, or about 18 pi cm * 1 cm = 18 pi cm^2.  

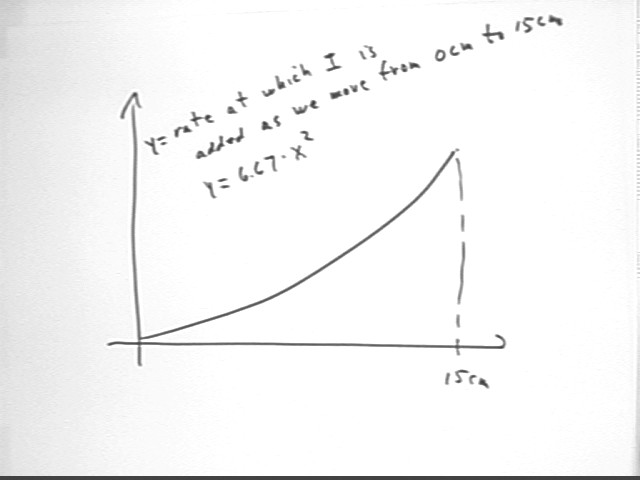
This ring would therefore have mass 18 pi cm^2 * .03 g / cm^2 = .54 pi grams, and we say that at r = 9 cm the mass is changing with increasing radius at the rate of .54 pi grams / cm.

Its moment of inertia would be .54 pi gram * (9 cm)^2 = 48.6 pi gram cm^2.

Moment of inertia per cm of radius at the r = 9 cm distance is therefore 48.6 pi gram cm^2, so at r = 9 cm moment of inertia is changing at the rate of [48.6 pi gram cm^2] / cm. 

• In symbols how much moment of inertia is there per cm of radius at the radial distance r?

At distance r the circumference is 2 pi r so as r increases the mass is changing at the rate of 2 pi r * density; an additional `dr of radius would result in the addition of approximately 2 pi r * density * `dr to the mass.

It follows that moment of inertia m r^2 would be increasing at the rate of 

• rate of mass change * r^2 = (2 pi r * density) * r^2 = 2 pi r^3 * density

in the sense that an additional `dr of radius will add approximately 2 pi r^3 * density * `dr to the moment of inertia.

• Sketch a graph of additional moment of inertia per cm of radius vs. r.

Additional moment of inertia per cm is thus 2 pi r^3 * density.  For the present example we therefore have

additional moment of inertia per cm = 2 pi r^3 * .03 g / cm^2 = .186 r^3 g / cm^2.

A graph is depicted below:

• What aspect of this graph tells you the total moment of inertia of the disk?

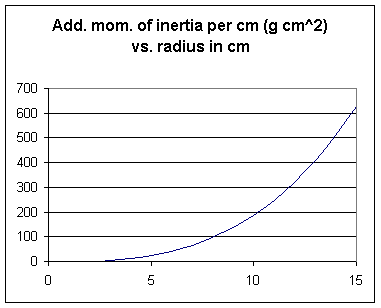
Graph altitudes represent additional moment of inertia per cm, the width of a trapezoidal region represents the number of cm by which radius changes.  So area represents additional I per cm of radius * cm of radius = additional I.  Adding up all such contributions yields the total moment of inertia, so that area under the curve represents the total moment of inertia.

• What therefore is the precise moment of inertia of this disk?

If we integrate .186 r^3 from r = 0 to r = 15 we obtain antiderivative .186 / 3 * r^4 = .062 r^4; between r = 0 and r = 15 this antiderivative changes by .062 * 15^4 = 3138, represent 3138 gram cm^2 or .0003138 gram cm^2.

Note criteria below for grading of lab reports:

1.  Gave the pertinent details of the setup.  10 pts.

2.  Stated what we were trying to observe or test.  10 pts.

3.  Reported sufficient and pertinent data.  10 pts.

4.  Told the reader what the data mean.  10 pts.

5.  Communicated the method of analysis.  20 pts.

6.  Analysis was correct and complete.  20 pts.

7.  Presented the desired final results in an appropriate organized form.  10 pts.

8.  Told the reader what conclusions were reached.  10 pts.