Physics I Quiz 1125
Problem Number 1A ball has a horizontal range of 5 meters when it is projected horizontally from an altitude of 25 meters. What will be its range if it is projected at an angle of 8 degrees above horizontal with the same initial speed? Approximately how much does its horizontal range change per degree from horizontal?
As with most projectile problems we want to find the `dt common to both vertical and horizontal motion, and we're going to analyze vertical and horizontal motion independently.
We know initial altitude and acceleration of gravity so we've got a good start with vertical motion.
We immediately note that we know the vertical displacement and the vertical acceleration. That's two of the five standard kinematic quantities.
In the first part of the problem the object is projected in the horizontal direction, so its initial vertical velocity is zero. This gives us v0y, `dsy and ay.
From v0, `ds and a we can use the 3d equation to find `dt and/or the 4th equation to find vf. We generally avoid the 3d equation for `dt because it's quadatic and therefore messy; however with v0 = 0 the third equation works just as easily as the fourth.
Using the 3d equation, and using the downward direction as the positive direction, we find that
`ds = v0 `dt + .5 a `dt^2, but with v0 = 0 we have
`ds = .5 a `dt^2, which we easily solve for `dt to get
`dt = +- sqrt( 2 `ds / a) = +-sqrt(2 * 25 m / (9.8 m/s^2) ) = +-2.3 sec.
We choose the positive `dt since only it makes sense.
To analyze the horizontal motion we note that acceleration in the horizontal direction is zero. We know that `dt = 2.3 sec, `ds = 5 m and a = 0.
Simply reasoning the situation out we have
vAve = `ds / `dt = 5 m / (2.3 s) = 2.2 m/s, approx..
Since a = 0 we know that v0 = vf = vAve, so init horiz velocity is 2.2 m/s.
Now if initial angle is raised to 8 degrees above horizontal, the vertical and horizontal motion are both affected. We have a nonzero initial velocity in the vertical direction, and the horizontal component of the initial velocity will be less than before.
We need to analyze vertical and horizontal motion separately. Since we're dealing with vector quantities at nonzero angles we use upward as the positive y direction, to the right as the positive x direction.
Analyze vertical motion first:
We know: vertical acceleration is
ay = -9.8 m/s^2, initial vertical velocity is
v0y = v0 sin(theta) = 2.2 m/s * sin(8 deg) = .3 m/s.
`ds = -25 meters. Change in position is final position - initial position; it doesn't matter what happens to position in between.
We can use the 3d eqn to find `dt or the 4th to find vf. The v0 `dt term is no longer zero and we don't want the pain of the quadratic so we use the 4th equation. The 4th equation, solved for vf, gives us
vf = +-sqrt(v0^2 + 2 a `ds) = +-sqrt((.3 m/s)^2+2* (-9.8 m/s^2) * (-25 m)) = +- 22.1 m/s.
Thus vAve = (-22.1 m/s + .3 m/s) / 2 = -10.9 m/s.
So `dt = `ds / vAve = -25 m/s / (10.9 m/s) = 2.3 s.
Having analyzed the vertical motion we proceed to the horizontal motion:
ax = 0, v0x = 2.2 m/s * cos(8 deg) = 2.18 m/s.
It follows that the horizontal displacement is
`dsx = v0x * `dt + .5 * ax * `dt^2 = 2.18 m/s * 2.3 s + 0 = 5.1 m.
Problem Number 2
If a mass of 3 kg moving at 9 m/s collides with a mass of 7 kg moving at -5 m/s, and the second mass has velocity -1.142857 m/s after collision, then what is the velocity of the first after collision? Is this collision possible for the system consisting of the two masses without the conversion of some internal source of potential energy?
We're given m1 and m2, as well as v1, v2 and v2'. From conservation of momentum we know that
m1 v1 + m2 v2 = m1 v1' + m2 v2'.
We can solve this for v1'.
v1' = (m1 v1 + m2 v2 - m2 v2 ') / m1 =
(3 kg * 9 m/s + 7 kg * (-5 m/s) - 7 kg * (-1.14 m/s) ) / (3 kg) =
( 27 kg m/s - 35 kg m/s + 8 kg m/s) / (3 kg) =
( (-8 kg m/s) + 8 kg m/s) ) / (3 kg) = 0.
Note that the -8 kg m/s in the numerator is the total momentum before collision and the +8 kg m/s is the negative of the momentum of the second object after collision.
Problem Number 3Sketch and label force diagrams for each of the following situations:
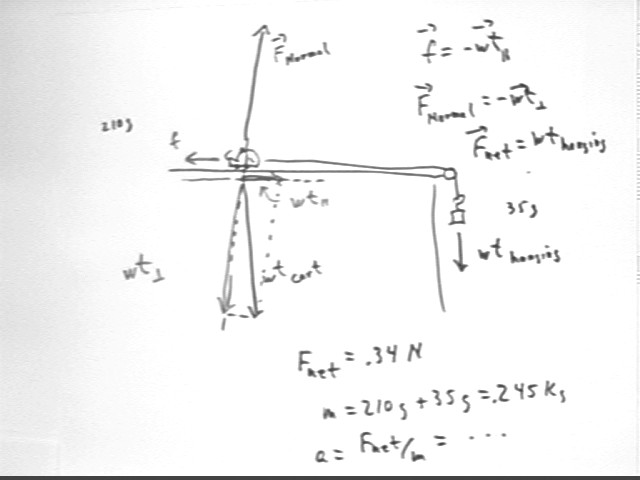
A mass of 35 grams is attached to a cart of mass 210 grams and suspended over a pulley of negligible mass and friction. The cart is placed on a ramp whose slope is just enough to compensate for the small frictional force acting on the cart. When the system is released, what will be the acceleration of the cart?
The figure below shows the forces acting on the system:

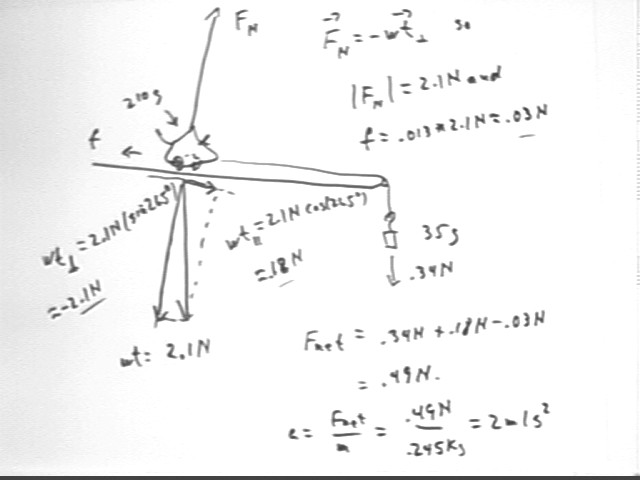
Answer the same question if the cart is placed on a ramp making an angle of 5 degrees with horizontal, with the cart being pulled down the ramp, and if the frictional force is .013 times the normal force on the cart.
In this case we can calculate the components of the weight vector. Using a set of coordinate axes with the x axis directed down the incline the parallel and perpendicular components of the weight are
The normal force is again equal and opposite to the perpendicular component of the weight. So Fnormal = 2.1 N. The frictional force is therefore .013 * 2.1 N = .03 N approx..
The net force is therefore .34 N - .03 N + .18 N = .49 N, approx..
The acceleration is thus a = F / m = .49 N / (.245 kg) = 2 m/s^2.
If after adding an unknown mass to the cart on the 5 degree incline the acceleration of the system is 18.86 cm/s^2, what is the unknown mass?
Note criteria below for grading of lab reports:
1. Gave the pertinent details of the setup. 10 pts.
2. Stated what we were trying to observe or test. 10 pts.
3. Reported sufficient and pertinent data. 10 pts.
4. Told the reader what the data mean. 10 pts.
5. Communicated the method of analysis. 20 pts.
6. Analysis was correct and complete. 20 pts.
7. Presented the desired final results in an appropriate organized form. 10 pts.
8. Told the reader what conclusions were reached. 10 pts.
Give the 'rotation wheel', with all the bolts inserted, a spin and take data to determine its initial angular velocity and its angular acceleration, assuming constant angular acceleration.
Take the data necessary to determine whether angular acceleration really is consistent at different angular velocities.
Measure the diameter of the axel.
Take the data you will need to determine initial angular velocity vs. angular acceleration for the wheel with the outermost four bolts removed.
Analysis: Figure out how much energy you put into the wheel for each spin and make a good estimate of how much torque you applied to get it spinning, as well as the force you had to exert to rotate the axle.
University Physics only
The density of a metal sphere with radius 15 cm, in grams / cm^3, is .7.5. The sphere is rotated about an axis thru its center.