
Physics I Quiz 1128
Problem Number 4Coasting from rest down a certain hill, whose slope is variable, I reach a speed of 15.81 m/s at the bottom. If I coast from rest down the second half of the hill I reach a speed of 5 m/s. Ignoring the effects of air resistance and friction:
The idea here is that the KE change down the entire hill, which is the result of PE loss, will be equal to the KE change down the first half plus the KE change down the second half. The information we are given allows us to determine the KE change down the entire hill and the KE change down the second half so we can easily determine the KE change down the first half.
Using A, B and C for the start, middle and endpoint of our trip we have the figure below.
We aren't given a mass so we assume mass M and go on in faith that the answer doesn't depend on mass, expecting M to cancel out at some point.

KE change is the result of PE loss. In the absence of information to the contrary we impicitly assume that `dWnoncons does not depend on velocity, so whatever is lost to friction is the same from A to B and from B to C on any run.
It follows that KE change between two points is the same for every run. That is KE change from b to c is the same for the first run as for the second (same PE loss, same `dWnoncons).
Therefore we have `dKEab + `dKE bc = `dKEac.
`dKEac = .5 M * (15.18 m/s)^2 = 115 M m^2/s^2
`dKEbc = .5 M * (5 m/s)^2 = 12.5 M m^2/s^2.
It follows the `dKEab = `dKEac - `dKEbc = 115 M m^2/s^2 - 12.5 M m^2/s^2 =102.5 M m^2/s^2.
Thus v at the end of the ab portion of the hill satisfies
.5 M v^2 = 102.5 M m^2/s^2
v = sqrt( (2 * 102.5 M m^2/s^2 ) / (M) ) = 14.4 m/s.
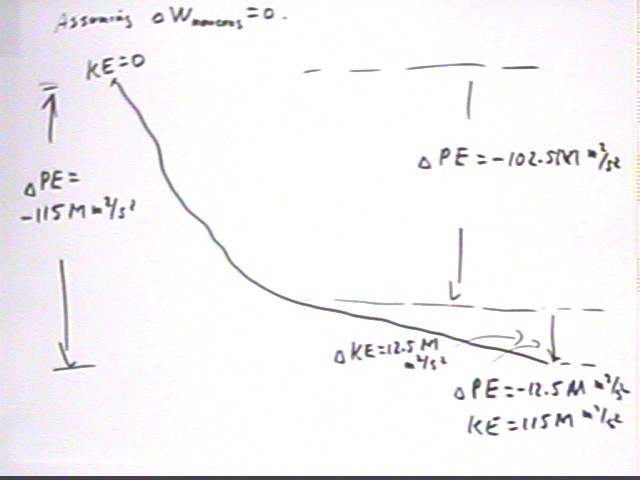
`dKE on the first half is 102.5 M m^2/s^2.
Assuming no friction, `dPE = -102.5 M m^2/s^2. This means that
M g `dy = -102.5 M m^2/s^2.
We get `dy = -102.5 M m^2/s^2 / (M * 9.8 m/s^2) = -10.4 m approx.
We therefore coasted 10.4 m vertically downward, and to go back up we would have to climb 10.4 m.
Problem Number 5Find the angular acceleration of the system if a torque of 1389 meter Newtons is applied to a system consisting of three concentric hoops constrained to rotate together about an axis through their common center and perpendicular to their common plane. Each hoop has a mass density of 5.934875 kilograms/meter, and the hoop radii are 11.19 meters, 22.38 meters and 33.57 meters.
Given torque, want angular acceleration. Newton's 2d Law says that torque = moment of inertia * angular acceleration so better find moment of inertia.
First find masses:
Each hoop has mass equal to the product of its mass density and its circumference. We get the following circumferences and masses:
hoop 1: circumference 2 pi * 11.19 m = 70 m, approx., and mass 70 m * 5.9 kg / m = 420 kg.
hoop 2: circumference 2 pi * 22.38 m m = 140 m, approx., and mass 140 m * 5.9 kg / m = 840 kg.
hoop 3: circumference 2 pi * 33.57 m = 210 m, approx., and mass 210 m * 5.9 kg / m = 1260 kg.
I = sum(mr^2). For each hoop the entire mass lies at the same distance r from the center.
hoop 1: mass = 420 kg, radius = 11.19 m so m r^2 = 420 kg * (11.19 m)^2 = 53,000 kg m^2.
hoop 2: mass = 420 kg, radius = 22.38 m so m r^2 = 840 kg * (22.38)^2 = 420,000 kg m^2.
hoop 3: mass = 420 kg, radius = 11.19 m so m r^2 = 1260 kg * (33.57 m)^2 = 1,400,000 kg m^2.
Total moment of inertia is 1,900,000 kg m^2.
A torque of 1389 m N results in acceleration
alpha = tau / I = 1389 m N / (1,900,000 kg m^2) = .0007 rad/s^2.
How long to get to 1 rad/s from rest?
If `d`omega = 1 rad/s then `dt = `d`omega / `alpha = 1 rad/s / (.0007 rad/s^2) = 1400 sec approx..
What is KE at 1 rad/s?
KE = .5 I omega^2 = .5 * 1,900,000 kg m^2 * (1 rad/s)^2 = 850,000 J, approx..
At what rate would energy have to be supplied to accomplish all this?
850,000 J in 1400 sec is about 600 Joules / sec.
Problem Number 6
A disk of negligible mass and radius 28 cm is constrained to rotate on a frictionless axis about its center. On the disk are mounted masses of 5 grams at a distance of 23.24 cm from the center, 20 grams data distance of 12.6 cm from the center and 47 grams at a distance of 10.92 cm from the center. A uniform force of .4988 Newtons is applied at the rim of the disk in a direction tangent to the disk.
Find I = sum(mr^2).
Torque of force is force * moment arm = .4988 N * .28 m = .14 m N.
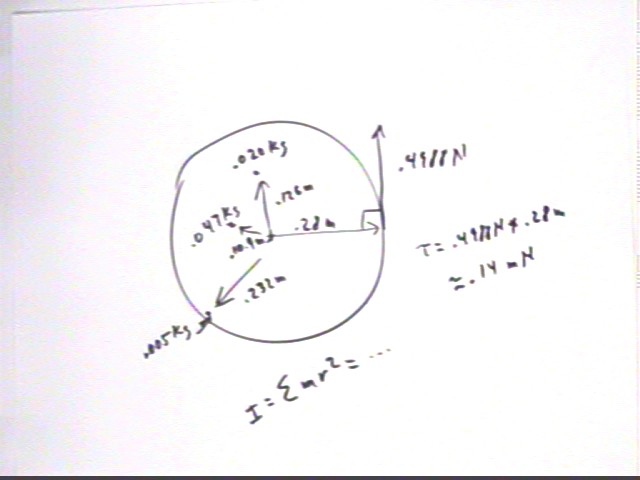
Just as `dW = F * `ds, we have `dW = tau * `d`theta.
`dKE = `dW so .5 I omega^2 = `dW from before.
Velocity of each mass is v = r * omega, where r is its distance from center. KE = .5 m v^2, where m is its mass.
If a mass hanging from the rim provides the torque then the weight of the mass is the .4988 N that supplies the torque.
The mass will descend so `dPE will be negative. The mass will descend until `dPE + `dKE = 0. We figured out `dKE above so we easily find `dPE of the hanging mass. From that we find `dy for the mass.
Problem Number 7
A small object orbits a planet at a distance of 20000 kilometers from the center of the planet with a period of 100 minutes. What is the mass of the planet?
The acceleration of the object is G M / r^2, where M is planet mass.
This is the centripetal acceleration.
Thus v^2 / r = G M / r^2 and
M = v^2 * r / G.
v = circumference / 100 minutes = 2 pi * 20,000,000 m / (100 min * 60 sec/min ) = etc.
Plug in and find M.
Problem Number 8
A person of mass 65 kg begins climbing a very high tower. The tower begins at the surface of the Earth, at a distance of 6400 km from the center, and rises to a position 2400 kilometers further from the center.