Notes from Class 1202

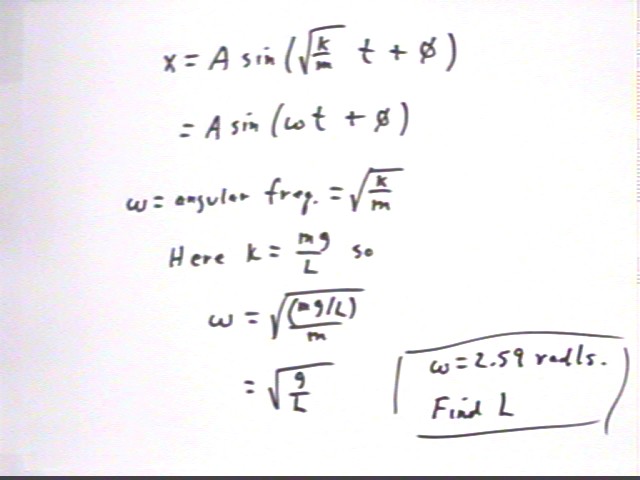
Physics I Experiment 1202

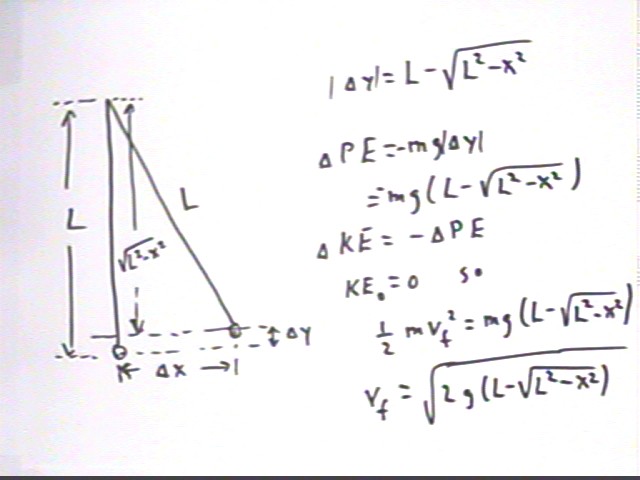
Using a paperclip or small coin on top of a cylindrical pendulum mass, obtain data which will allow you to determine the velocity of a pendulum at equilibrium vs. x  when released from rest at displacement x from equilibrium.

Figure out the velocity of the pendulum based on your observations of the motion of the paperclip or coin.

Figure out the velocity the pendulum should attain based on the length of the pendulum and the pullback.  Use conservation of energy and the figure below:

We observed the synchronization of a pendulum with a simulation consisting of the vertical projection of a point moving in a circular path.  To 3 significant figures the angular frequency of this motion was found to be 2.59 rad/s.  We will use this to predict the length of the pendulum.

The next figure shows the forces acting on the pendulum of length L when displaced horizontally a distance x from its equilibrium position.   When the pendulum is swinging freely these forces include the weight m g acting vertically downward and the tension T acting in the direction of the string.  The tension is shown, as well as its components Tx and Ty.

• For small displacements x we have near-equilbrium in the y direction (very little acceleration in the y direction, with y acceleration near zero when x is near zero), and the y component is very close in magnitude to the tension itself.
• Since we have near-equilibrium in the vertical direction Ty must be very nearly equal and opposite to the weight, which means that Ty = m g and therefore T = mg, to a good approximation.
• The similarity of the triangles shown at lower left tells us that | x / L | = | Tx / T |.
• Since T is very close to mg, and since Tx  we have Tx = - (m g / L) * x.

Tx is the net force acting on the pendulum, again to a very good approximation if x is small compared to L.

Fnet = Tx = - (m g / L) * x is of the form Fnet = - k x with k = -m g / L.

Since Fnet = m a it follows that

• m a = - k x.

Applying Calculus (General College Physics and Principles of Physics students should understand everything up to this point) we have a = x '', where the differentiation is with respect to clock time t, so that

• m x '' = - k x or
• x '' = -k /m * x.

The only functions whose second derivatives are negative multiples of itself are the sine and cosine functions.  Calculus-literate students can easily verify that x

•  x = A sin( sqrt(k / m) * t + phi)

is a solution for any A and any phi.  This solution can be written

• x = A sin(omega * t + phi),

where omega is the angular frequency of the motion.

Back to the non-calculus world we use the following result of the above:

• An object which experiences a linear net restoring force of the form F = - k x undergoes motion dictated by the equation

• x = A sin(omega * t + phi),

• where omega = sqrt(k / m) is the angular frequency of the motion.  We will deal with A and phi later.

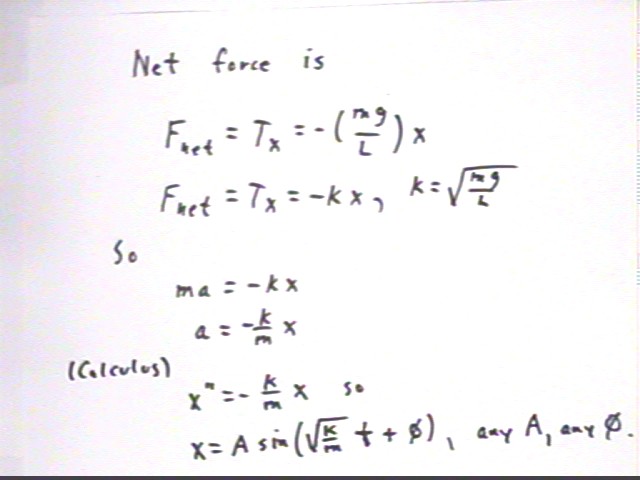
Using the fact that omega = sqrt(k / m), and the fact that for our pendulum k = m g / L, find from the fact that omega = 2.59 rad/s the length L of the pendulum.  We'll check this against reality next class.