Notes from Class 1204

Physics I Quiz 1204

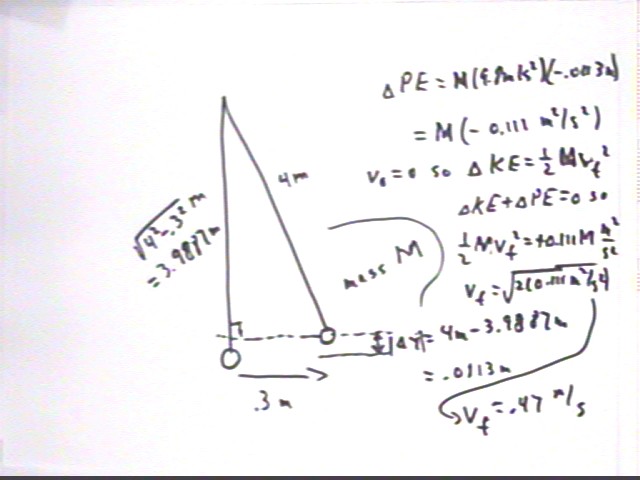
Using energy considerations find the maximum velocity of a simple pendulum of length 4 meters which is pulled back 30 cm.

Using right triangles with the figure below we find that `dy = -.0113 m, so that `dPE = M * 9.8 m/s^2 * `dy = -.111 M m^2/s^2.

`dKE = -`dPE and `dKE = .5 M vf^2 so

.5 M vf^2 = .111 M m^2 / s^2.  We solve for vf, obtaining vf = .47 m/s, approx..

The angular frequency of a certain pendulum is 3.22 rad / sec.  Recall that omega = sqrt(k / m) and for a pendulum k = m g / L.

• How long does it take this pendulum to complete a cycle?

To complete the 2 pi radians corresponding to a complete circle, moving at 3.22 rad/sec, requires `dt = 2 pi rad / (3.22 rad/s) = 1.95 sec.

• What is the length of this pendulum?

Using omega = sqrt(k/m) and k = m g / L we find that L = .945 meters.

• If the amplitude (amplitude is maximum displacement from equilibrium) of the pendulum's motion is 6 cm then what is the radius of the circle required to model the motion of the pendulum?

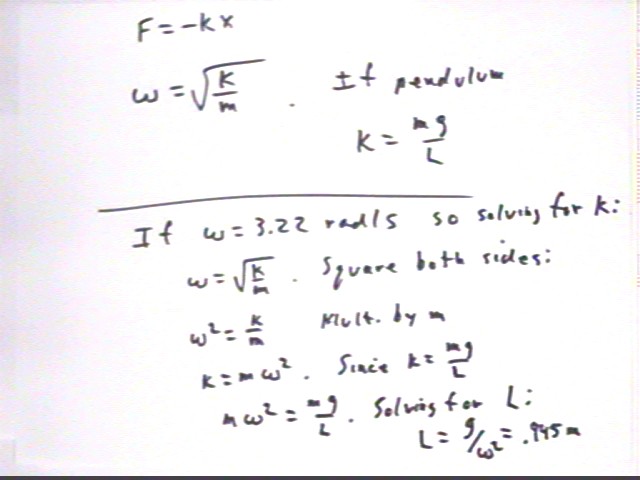
A circle of radius 6 cm gives us a vertical projection line with an amplitude of 6 cm on either side of the center.

• What is the velocity of the point moving around the reference circle for this pendulum?

The point moves at 3.22 rad/s on a circle of radius 6 cm.

6 cm corresponds to 3.22 rad * 6 cm = 19.3 cm, so the point moves at 19.3 cm/s.

The figure below shows how we might use energy considerations to find a similar result for displacement .3 meters.