Physics Quiz 1209
The centripetal acceleration of the reference point is always directed toward the center of the circle.
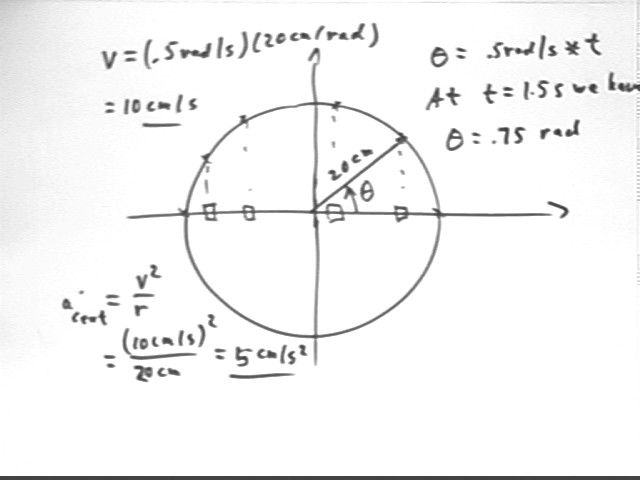
For motion at .5 rad/s, starting at theta = 0 when t = 0 on a reference circle of radius 20 cm:
The centripetal acceleration is aCent = v^2 / r.
The reference point is moving at .5 rad / s * 20 cm / rad = 10 cm / s, so
aCent=v^2/r = (10 cm/s)^2 / (20 cm) = 5 cm / s^2.

At t = 1.5 sec we have theta = 1.5 sec * .5 rad / s = .75 rad.
The centripetal acceleration is directed toward the center of the circle, at 180 deg or pi rad from the .75 rad direction. The angle is therefore .75 rad + pi = 3.89 rad.
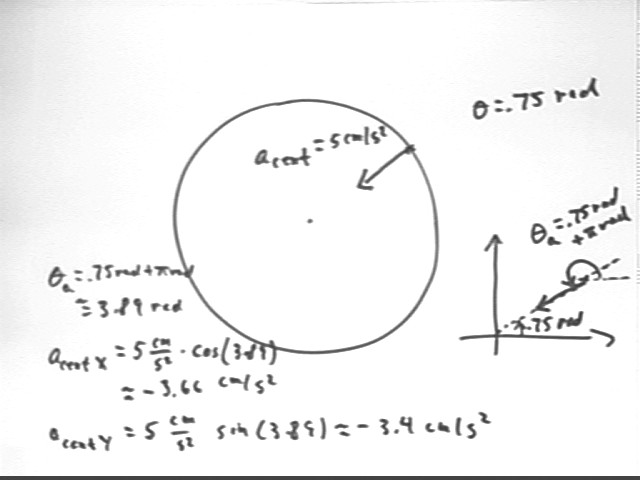
The x and y components components, illustrated in the figure below, are found from the magnitude 5 cm/s^2 and angle 3.89 rad of the centripetal acceleration vector:
This means that for a pendulum modeled by the x component of the reference-circle motion we have at t = 1.5 sec acceleration -3.66 cm/s^2.
In general for reference circle radius A, ang vel omega and init ang position phi we see that the velocity of the reference circle point is v = omega * A and the centripetal acceleration of that point is aCent = v^2 / r = omega^2 * A.
So the x component of the motion is characterized by
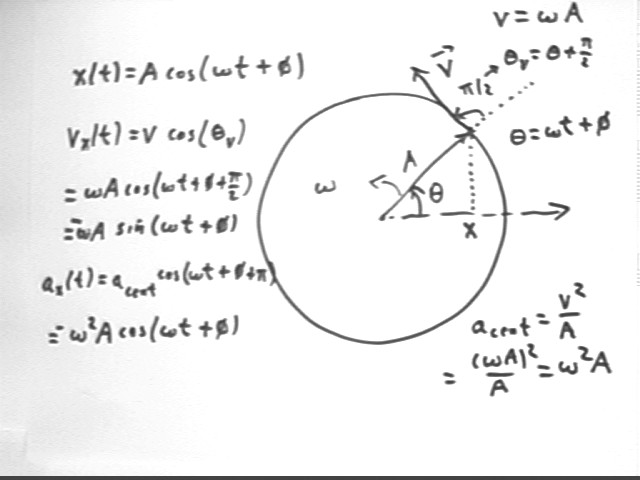
The two figures below indicate the position, velocity and acceleration functions corresponding to the horizontal and vertical coordinates of the reference-circle motion.
We note that in each case that the velocity v is the first derivative with respect to t of the position function, and acceleration a is the second derivative.


Answer the following questions relating motion on the reference circle to the motion of a pendulum:
The figure below depicts, more or less accurately, a number of equally spaced points on the reference circle. We see that the magnitude of the change in x position between two points is greatest near the y axis, indicating that the x velocity is greatest when the reference circle position is near pi/2 or 3 pi/2 radians. So the velocity of an object modeled by the x position of the reference-circle point has its greatest magnitude at these points.
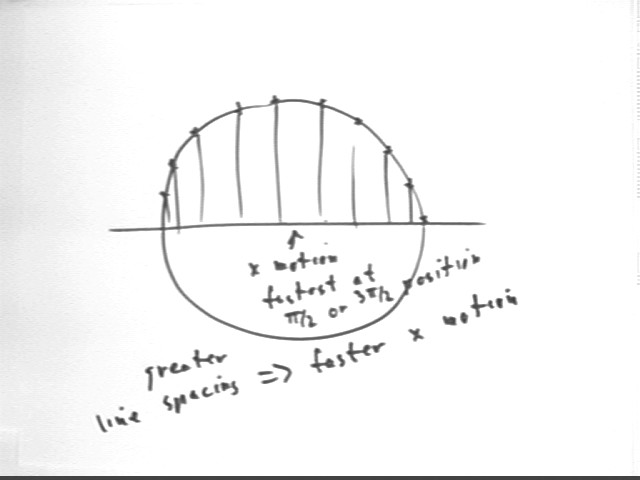
Alternatively we can see that the velocity vector for the reference-circle point is parallel to the x axis at the pi/2 and 3 pi/2 points so that the x velocity at each of these points has magnitude equal to the speed of the reference-circle point. At every other point the s component of the reference-circle velocity is less in magnitude than the reference-circle speed.
At the pi/2 and 3 pi/2 points we see that x = 0--that is, the object is at its equilibrium position.
At these points we also see that the centripetal acceleration vector is vertical, with x component 0. This indicates that at these points the acceleration of the object modeled by the x component of the reference-circle position is 0.
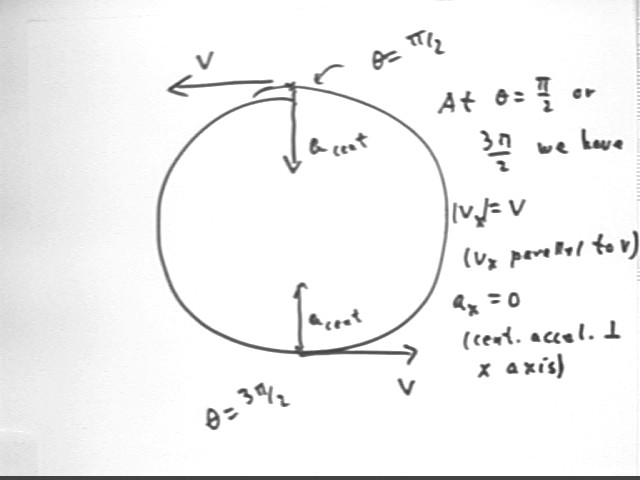
The x component of the reference-circle velocity will be 0 when the velocity vector is vertical.
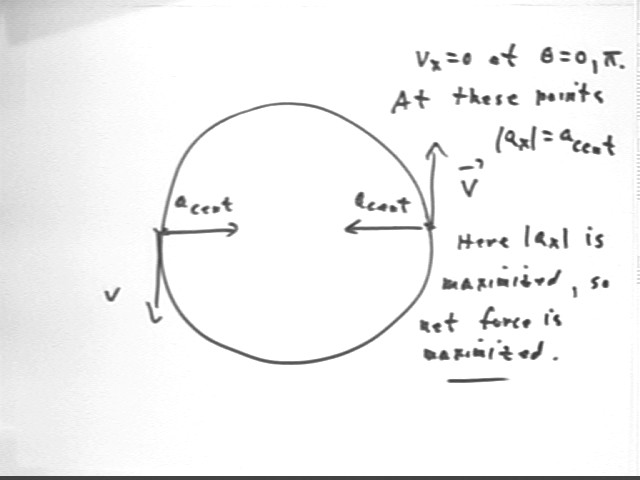
The figure below shows where this occurs, at the 0 radian and pi radian positions. At these positions the x coordinate is at its maximum distance A from the equilibrium position.
We note that the centripetal acceleration vectors are in the x direction, pointing directly back toward the equilibrium position. It is therefore at these points where the acceleration of the x component is maximized.
This agrees with the fact that the maximum force on a pendulum occurs at the extreme points, where the angle of the tension vector is maximized with the resulting maximum magnitude of the horizontal force.
We have seen that at the pi/2 and 3 pi/2 positions, corresponding to the equilibrium position, the acceleration is zero and the magnitude of the velocity is maximized.
We will be discussing energy considerations during the next class.
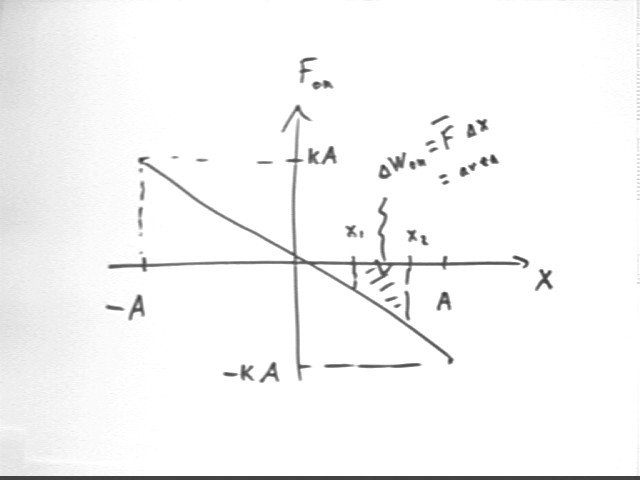
We note that the force exerted ON the system by the elastic restoring force F = - k x can be depicted by the graph below.
Between two positions x1 and x2 we can calculate the work done ON the system by this net force. If | x2 | > | x1 | -- i.e., if we are moving further from the equilibrium point -- then the direction of motion is opposite the direction of the force (which is back toward equilibrium) and hence the work done by the force is negative.
The average force can be represented by the average 'height' of the graph and the displacement by x2 - x1, so the 'area', which here is negative, represents the work done ON the system.
We note that if | x2 | < | x1 | then we are moving in the same direction as the force and the work is the negative of the negative area, or positive.
The work being done BY the system is therefore positive when we move away from the equilibrium position and negative when we move toward the equilibrium position. Since this work is done against a conservative force the PE of the system increases as we move out and decreases as we move back. Of course we know this since the pendulum rises as we move outward and descends when we move inward.
In the idea situation no nonconservative forces act so that the work-energy theorem tells us that
indicating that as we swing out the increasing PE is associated with decreasing KE, and vice versa.
The work required to move the pendulum from equilibrium to displacement x from equilibrium is easily seen to be .5 k x^2. So the PE at position x is PE(x) = .5 k x^2.

Remember also that when Fnet = - k x we obtain angular frequency