Notes from Class 1211

Physics Quiz 1211

Find the velocity, acceleration and position functions for a pendulum modeled by the x coordinate of the reference circle point if we know that the reference-circle point starts at the theta = 0 position when t = 0, and that the amplitude of the motion is 12 cm.  The angular frequency of the pendulum is 2.59 rad / s and the mass of the pendulum is 1 kg.

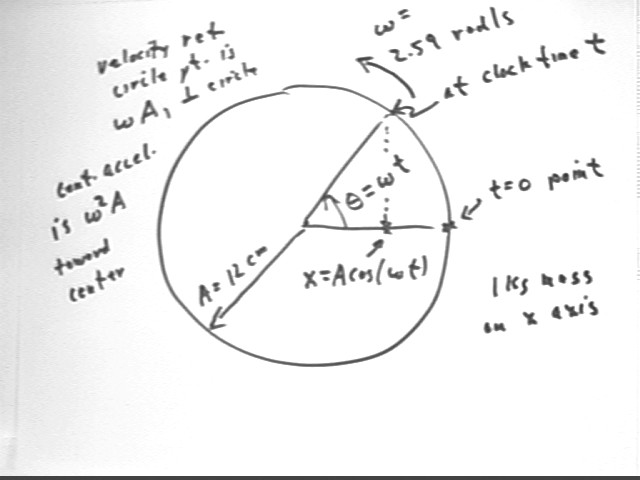
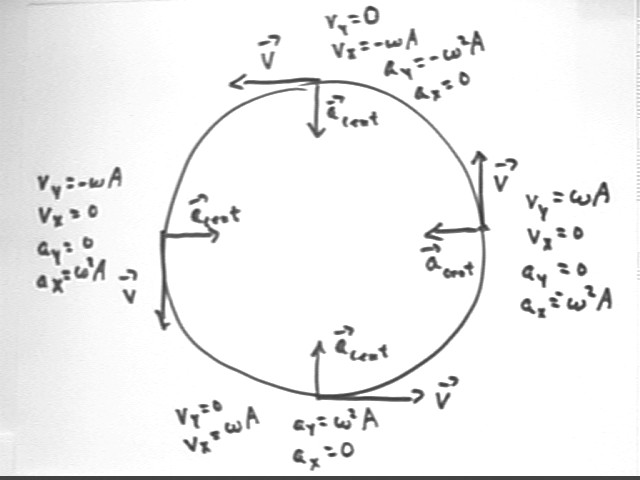
The figure below indicates the given characteristics of the circular model.  The radius of the circle corresponds to the amplitude and the angular velocity of the point around the reference circle is the angular frequency of the SHM.  Consistent with the given characteristics the initial angular position is at theta = 0.

The position of the pendulum is given by the x coordinate A = A coms(omega * t).

The velocity of the point on the reference circle is omega * A, always perpendicular to the circle, and its centripetal acceleration is omega^2 A, of course toward the center of the circle.

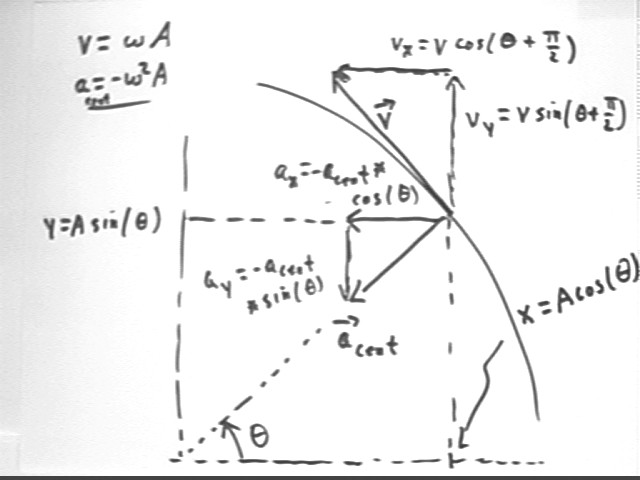
The figure below shows the motion at an arbitrary instant.  The angular position of the reference point is theta = omega * t.  The velocity of the point on the reference circle has magnitude v = omega * A and is directed at angle theta + pi/2 so its components are vx = v cos(theta + pi/2) and vy = v sin(theta + pi/2).  Noting that v = omega * A,  cos(theta + pi/2) = -sin(theta) and sin(theta + pi/2) = cos(theta) we have

• vx = omega A * sin(theta) and
• vy = omega A * cos(theta).

The centripetal acceleration vector aCent has magnitude v^2 / r = v^2 / A = (omega * A)^2 / A = omega^2 * A and direction exactly opposite theta, so that 

• ax = -omega^2 * A * cos(theta)  and
• ay = -omega^2 * A * sin(theta).

The resulting functions are summarized below:

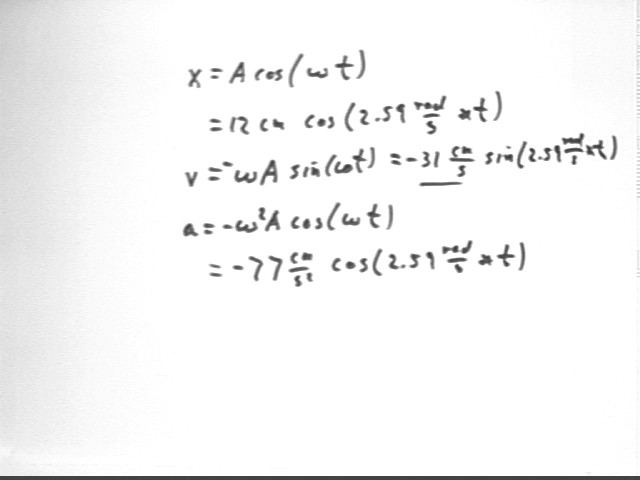
Use these functions to answer the following:

• What are the speed and acceleration of the pendulum at its extreme points?

A = 12 cm and omega = 2.59 rad/s so that 

• v = omega * A = 2.59 rad/s * 12 cm = 31 cm/s, approx., 

and 

• aCent = omega^2 * A = (2.59 rad/s)^2 * 12 cm = 77 cm/s^2, approx. (this mental approximation is off a bit so you should correct this error).

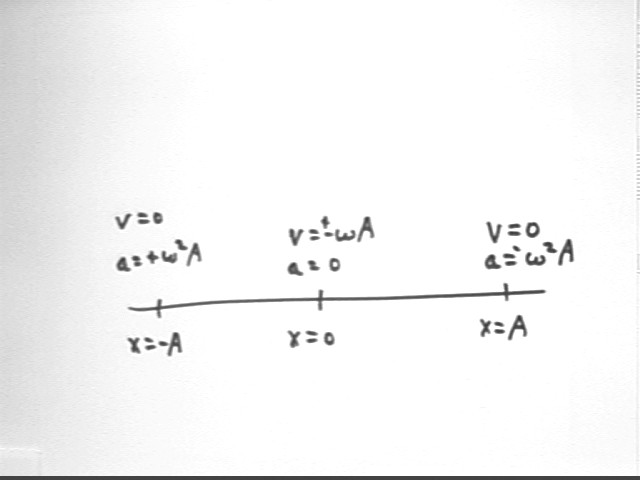
We have from our equations for x, vx and ax: 

• x = 12 cm cos(2.59 rad/s * t)
• vx = -31 cm/s sin(2.59 rad/s * t)
• ax = -77 cm/s^2 cos(2.59 rad/s * t)

We draw the conclusion that at extreme points v = 0 in one of two ways:

• At extreme points (far right and far left on reference circle) speed is zero (velocity vector is vertical, zero horiz component).
• At extreme points x = 12 cm cos(2.59 rad/s * t) takes its extreme value +12 cm or - 12 cm.   At these points cos(2.59 rad/s * t) = 1 or -1.  

When cos(2.59 rad/s) = +-1 then sin(2.59 rad/s * t) = 0.  It follows that 

• v = -31 cm/s sin(2.59 rad/s) is zero.  

It also follows that 

• a = -77 cm/s^2 * cos(2.59 t) will have magnitude 77 cm/s^2.

• What are the speed and acceleration of the pendulum at its equilibrium point?

At equilibrium point we have two models, as before:

• Reference point is at 'top' or 'bottom' of circle so the velocity of the ref-circle pt is parallel to the x motion, and the centripetal acceleration vector (toward the center of the circle) is vertical.  Thus the x component of velocity has magnitude equal to ref-circle velocity (31 cm/s) and the x component of acceleration is zero (vertical accel vector has zero x component).
• In terms of the equations, at equilibrium the net force is zero so acceleration is zero.  It follows that a = -77 cm/s^2 cos(2.59 rad/s * t) = 0 so that cos(2.59 rad/s * t) = 0.  

It then follows that x = 12 cm cos(2.59 t) is also 0.  

It also  follows that | sin(2.59 t) | = 1 so that v = -31 cm/s sin(2.59 t) is maximized. 

The figure illustrates how these ideas apply at the theta = 0 and theta = pi points of the graph.  

• At theta = omega t = 0 we have cos(omega t) = 1 and sin(omega t) = 0 so that 

x = A, y = 0, | a | = omega^2 * A, centripetal accel is omega^2 * A so centripetal force is F = m a = m * omega^2 * A.

• At theta = omega t = pi/2 we have cos(omega t) = 0 and sin(omega t) = 1 so that 

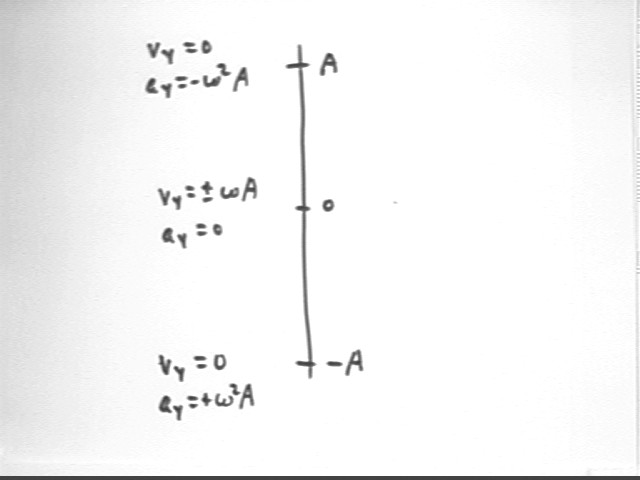
x = 0, y = A, | a | = omega^2 * A, centripetal accel is omega^2 * A so centripetal force is F = m a = m * omega^2 * A.

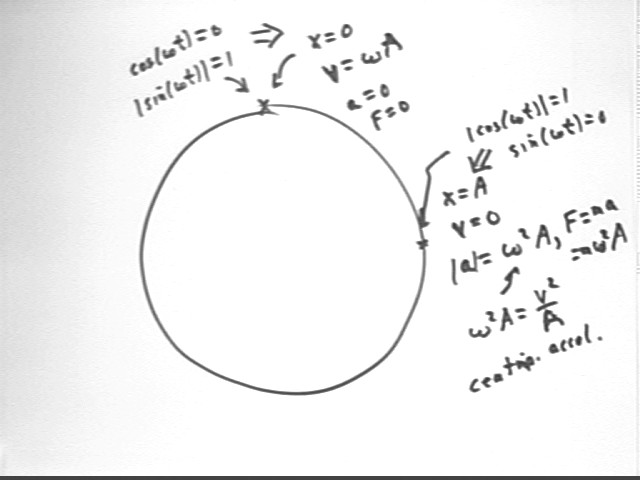
The figure below indicates many of the properties of the circular model at the points where magnitude of position, velocity or acceleration is zero.  Both x and y quantities are given.

Motion in the x direction at these points is as indicated in the figure below.  

• At x = A we have vx = 0 (indicated here just v =0, since we are now talking just about x motion) and a = - omega^2 * A.  
• At x = 0 we have a = 0 and the magnitude of v is equal to its maximum omega* A, so that v = +- omega * A (positive when the pendulum is moving to the right, negative when moving to the left).
• At x = - A we again have v = 0, with a = +omega^2 * A.

y motion can be similarly summarized at the equilibrium and end points.

• How much restoring force is exerted on the pendulum at its extreme points?

At extreme points | a | = 77 cm/s^2 so | F | = m | a | = 1 kg * .077 m/s^2 = .077 Newton.

• How much KE does the pendulum have at equilibrium?

v at equilibrium is 31 cm/s = .31 m/s so KE at equilibrium is .5 m v^2 = .5 * 1 kg * (.31 m/s)^2 = .05 Joule.

Explain in terms of the reference-circle model why your answers are valid.

What is the restoring-force constant k for this pendulum?  What therefore is its potential energy at its extreme position?

Restoring-force constant is found from omega = sqrt(k/m):  k = omega^2 * m = (2.59 rad/s)^2 * 1 kg = 6.7 N / m or .067 N / cm

Force at extreme position is .067 N/cm * 12 cm = .8 N approx..  Force increases linearly from 0 to .8 N as we displace the pendulum 12 cm = .12 m from equilibrium to extreme position.

Thus `dW = Fave * `ds = (0 + .8 N) / 2 * .12 m = .048 J.  This is the PE at the extreme point.

This agrees within roundoff with the .05 Joules we obtained for the KE at equilibrium.

What is the potential energy of this pendulum at position x = 6 cm relative to the equilibrium point?  What therefore is its KE at this point?

PE at position x is work to displace from equil to x.  Force at x is k x, force at equil is 0 and force is linear in x so Fave = (0 + kx) / 2 = 1/2 k x.  Displacement is x so `dW = Fave * `dx = 1/2 k x * x = 1/2 k x^2.

So PE at x = 6 cm is 1/2 (6.7 N/m) * (.06 m)^2 = .012 J.

At the 6 cm position, if released from max displacement, the PE will decrease from .048 J to .012 J.  So `dPE = -.036 J and `dKE = + .036 J.

We can solve .5 m v^2 = .036 J for v.