
Physics Quiz 1213
A mass oscillates at the end of an ideal spring. The force constant for the spring is k = 100 N / m and the frequency of oscillation is 2 cycles per second. What is the mass of the object?
We have k and frequency, so we can use omega = sqrt(k / m), which we solve for m to get m = k / omega^2.
A cycle is 2 pi radians so 2 cycles is 4 pi radians. Substituting k = 100 N /m and omega = 4 pi rad / sec, we get
This solution is shown in the top half of the figure below.

What restoring force constant is necessary if a mass of 4 kg is to undergo SHM with a period of .2 seconds?
This solution is outlined in the bottom half of the figure above.
From mass m and angular frequency omega we can find k = m omega^2 (solve omega = sqrt(k/m) for k).
We are given mass; from the given period, or time required to complete 1 cycle, we can find the angular frequency (number of rad / sec).
We have m = 4 kg period .2 sec.
Period .2 sec means we undergo a complete cycle of 2 pi radians in .2 sec, so that angular frequency is 2 pi rad / (.2 sec) = 10 pi rad/sec.
Plugging omega = 10 pi rad/s and m = 4 kg into k = m * omega^2 we find that k = 4000 N /m, approx..
The restoring force constant of a pendulum of length L is m g / L. What is the period T of this pendulum?
Given k = m g / L and mass m we get
Period is time required to go thru 2 pi radians at angular velocity omega:
2 pi / sqrt(980 cm/s^2) = .2007 approx.
So if L is in cm then

Given the restoring force function Fnet = - k x, what is the average force exerted between displacements A and x relative to the equilibrium position? How much work by the restoring force is done in moving from position A to position x?
Force at displacement x is F = - k x; force at displacement A is F = - k A. Averaging the two forces, which since the force is a linear function of position, gives us an exact result for ave force. We get
The displacement from position A to position x is x - A so that the work done is
Note that if x < A, as must be the case if A is the amplitude of the SHM, both the force and the displacement are in the same direction so the work done by the restoring force is positive.
Note also that this is the work done ON the pendulum by a conservative force. The work done BY the pendulum against this force is the change `dPE in the potential energy of the pendulum, and is equal to the opposite of the work done ON the pendulum. So we have
University Physics Students: Using the general expressions x = A cos(omega * t + phi) and vx = omega A sin(omega * t + phi) verify that at any clock time t we have v = sqrt( k ( A^2 - x^2) / m ).
Substituting vx = omega A sin(omega * t + phi) for v and x = A cos(omega * t + phi) we obtain
omega A sin(omega * t + phi) = sqrt(k (A^2 - (A cos(omega * t + phi))^2 / m) = sqrt(k(A^2 - A^2 cos^2(omega * t + phi))/ m. Squaring both sides of this equation gives us
Dividing both sides by omega^2 A^2 we have
or
This is the Pythagorean Identity, proving that v = sqrt(k (A^2 - x^2) / m) is consistent with the equations of motion.
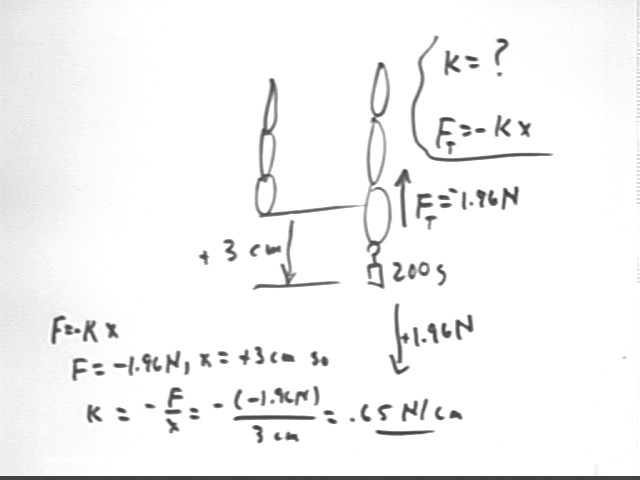
If adding a 200 gram hanging mass to a rubber band stretches the rubber band by 3 cm then, assuming F = - k x for the rubber band (a questionable assumption as we have seen), then approximately what is the force constant for the rubber band?
F = - k x. When x = 3 cm we find that F supports a 200 g mass against gravity so that F = -.2 kg ( 9.8 m/s^2) = -1.96 N and
k = -F / x = .65 N / cm.
How many cycles should the system undergo in 5 seconds?
Each cycle corresponds to 2 pi radians so we have
In 5 second we would therefore expect 2.8 cycles/sec * 5 sec = 14 cycles.

Quick Experiment:
Using one chain of 3 series-connected rubber bands for every 250 grams of a hanging mass, with the chains working in parallel, determine the force constant k and the angular frequency omega of the harmonic motion of the mass when suspended from the rubber-band combination.
Verify the relationship omega = sqrt( k / m).
Observations yielded a stretch of about 5 cm for a 200 gram mass, meaning a 5 cm stretch results in a force of .2 kg * 9.8 m/s^2 = 1.96 N. The force constant is therefore around 1.96 N / (5 cm) = .4 N / cm for a single strand of 3 rubber bands in series.
For a 200 gram mass this would yield, by a calculation almost identical to that done above,
and would predict about 11 cycles in 5 sec.
For two parallel strands with a 500 g mass we got force constants around .8 N / cm, which would yield angular frequency omega around 12.7 rad/s and 10 cycles / sec.
Summary of SHM:
SHM occurs when Fnet = - k x acts on a constant mass m.
This can occur for a pendulum or a mass on a spring.
The angular frequency of the SHM is omega = sqrt(k / m), obtained using calculus to obtain the solution to the differential equation m x '' = - k x. This equation is obtained from Fnet = - k x, since Fnet = m * a = m * x ''.
SHM can modeled as either the x or the y coordinate of a point moving on a reference circle.
On a reference circle of radius A with angular position phi at t = 0 we have the coordinates
Having the functions for x and y we can use calculus to easily determine the velocity and acceleration functions. This can also be done without calculus. University Physics students should be able to verify that calculus gives the same results as those given below:
The velocity and acceleration of the point on the reference circle are v = omega * A in the direction tangent to the circle, and aCent = v^2 / r = v^2 / A = omega^2 * A. The components of the velocity in the x and y direction are
The components of the acceleration are
Energy in SHM
The work required to extend the oscillator from equilibrium to distance x from equilibrium is
This is the work done ON the system by the displacing force. The work is done against the conservative force F = - k x, so this work is the increase in the PE of the oscillator.
When the system is released, if the only force acting on the system is the restoring force F = - k x then as the system moves from displacement A to displacement x the average force exerted ON the system is Fave = (- k x - k A) / 2 = - k ( x + A) / 2 and the displacement is x - A so the work done ON the system BY the conservative force is
It follows that the work done BY the system AGAINST the conservative force is
Since F is a conservative force we therefore have
Since A is the maximum displacement from equilibrium | A | > | x | and A^2 - x^2 is positive so -1/2 k ( A^2 - x^2) is negative. That is, from displacement A to displacement x the PE decreases. Since we assume that no nonconservative force acts on the system `dWnoncons = 0 and the decreasing PE will be associated with an increase in KE.
Between position A and position x we have `dPE + `dKE = 0 and
At displacement A the velocity is zero so KE0 = 0; therefore the KE at position x is
Velocity at position x is found by setting .5 m v^2 equal to KE:
so velocity at position x is
University Physics students should be able to verify this relationship using the equations of motion for either the x or the y motion (e.g., substitute the expression for vx in place of v and the expression for x in place of x and simplify to show that the equation is an identity).
Problem Number 1If a simple pendulum of mass 1.159 kg and length 75 cm is moving at 81 cm/s as it passes through the low point of its arc, what its its angular velocity about its pivot point at that instant? What is the tension in the string of the pendulum?
A radian is an arc distance equal to the radius.
An arc distance of 75 cm corresponds to 1 radian.
81 cm/s corresponds to (81/75) rad / s = 1.08 rad/s.
The net force on the pendulum is equal to the centripetal force acting on it.
The net force is equal to the vector sum of the tension force and the gravitational force. Using the upward direction as positive we note that Fcent, directed toward the center of the circle, is positive and the gravitational force m g is negative. So we have
Problem Number 2
A grinding wheel in the shape of a uniform disk of radius 23 cm is rotating at 790 revolutions per minute. The total mass of the wheel is 1.9 kg, which is uniformly distributed. A piece of steel is pressed in the normal direction against the wheel with a force of 12 Newtons. The coefficient of friction between steel and wheel is .39. How long will it take the wheel to stop?
The wheel has moment of inertia I = .5 M R^2 = .5 * 1.9 kg * (.23 m)^2 = .06 kg m^2, approx..
The frictional force is .39 * 12 N = .48 N, approx., and being directed perpendicular to the tangent to the circle exerts a torque of magnitude .48 N * .23 m = .11 m N, approx..
The angular acceleration of the system is torque / moment of inertia:
| alpha | = | tau | / I = .11 m N / (.06 kg m^2) = 1.8 rad / s^2, approx..
If our original angular velocity of 790 rev / minute = 790 * 2 pi rad / (60 s) = 77 rad / s then the acceleration, being opposed to motion, must be negative.
We have omega0 = 77 rad/s, alpha = -1.8 rad/s^2 and omegaF = 0 so
`dt = `d `omega / alpha = (0 - 77 rad/s) / (-1.8 rad/s^2) = 43 sec, approx..
Problem Number 3
A pendulum is released from rest at a displacement of .47 meters from its equilibrium position. It is stopped abruptly and uniformly at its equilibrium position and it is observed that a loose bit of metal slides without resistance off the top of the pendulum and falls to the floor .89 meters below.
The projectile begins with vertical velocity 0 and falls .89 meters in the vertical direction with vertical acceleration 9.8 m/s^2. The time required for fall is therefore `dt = sqrt(2 * .89 m / (9.8 m/s^2) ) = .4 sec, approx.. The horizontal velocity is constant so initial horizontal velocity is .35 m / (.4 sec) = .9 m/s, approx..
At position x we have v = sqrt( k ( A^2 - x^2) / M), where M is the mass of the pendulum.
At equilibrium x = 0 so we know that sqrt(k ( A^2 - 0^2) / M) ) = .9 m/s so that sqrt( k A^2 / M ) = .9 m/s and therefore k / M = (.9 m/s)^2 / A^2 = .81 m^2/s^2 / (.47 m)^2 = 3.7 s^-2.
Therefore when x = .17 m we have v = sqrt( k / M ( A^2 - x^2) ) = sqrt( .37 s^-2 ( (.47m)^2 - (.17 m)^2 ) ) = sqrt(.071 m^2/s^2) = .27 m/s.
Problem Number 4
A Ferris wheel with radius 21 meters is moving fast enough that at the top of its arc a 150-lb person at the rim of the wheel has an apparent weight of only 99 pounds.
99/150 = .6 approx. so the person's apparent weight is only .6 of actual weight. The actual weight of the person is m * g so the force exerted by the seat is .6 m g.
Apparent weight is the force between the person and the seat. The net force on the person is
Fnet = force exerted by seat + force exerted by gravity.
The force exerted by the seat is upward and the force by gravity is downward so choosing upward as the positive direction we have
Fnet = force of seat - m g = .6 m g - m g = -.4 m g.
The net force acting on any object moving in a circle is equal to the centripetal force on that object so we know that Fnet = m * v^2 / r; at the top of the Ferris wheel the center is directly below so this force is exerted in the downward direction. Thus
-m v^2 / r = -.4 m g and
v = sqrt(.4 g * r) = sqrt(.4 * 9.8 m/s^2 * (21 m) ) = sqrt( 82 m^2/s^2) = 9 m/s.
At the bottom of the arc the net force will be upward and the weight downward so we have
Fnet = + m v^2 / r = force of seat - m g so that, noting that v m^2 / r is still equal in magnitude to .4 m g
apparent weight = force of seat + m g + m v^2 / r = m g + .4 m g = 1.4 m g = 1.4 * actual weight = 1.4 * 150 lb = 210 lb.
At the center of the wheel the force exerted by the seat has components .4 m g toward the center and m g upward; the resultant force is sqrt(( .4 m g )^2 + (m g)^2 ) = 1.07 m g =1.07 * 150 lbs = 161 lbs approx.. This assumes that the seat structure is light and free to 'swing' on an axis thru the rim of the wheel so that the entire force exerted by the seat will be a normal force.
Problem Number 5
A person is being rotated in a horizontal circle of radius 11 meters. If the person feels a centripetal force of 5.9 times her own weight, how fast is she traveling? code `t
The centripetal force will by 5.9 * weight = 5.9 * m * g, where m is the mass of the person.
Centripetal force is m v^2 / r so we have
m v^2 / r = 5.9 m g,
which we solve for v to obtain
v = sqrt( 5.9 g r ) = sqrt( 5.9 * 9.8 m/s^2 * 11 m) = sqrt( 636 m^2/s^2) = 25.2 m/s approx.
Problem Number 6A simple harmonic oscillator has a restoring force of 170 N/m and a mass of .67 kg. It is given a KE of .2457 Joules at a point .0447 meters from equilibrium.
The total energy of the oscillator at this point is
Max displacement from equilibrium occurs when all energy is potential energy:
The equation of motion is x = A cos(omega * t + theta0), where omega is angular frequency, A is amplitude and theta0 is initial angular position on the reference circle.
We found that A = .056 m.
omega = sqrt(k / m) = sqrt( 170 N/m / (.67 kg) ) = 15.9 rad/s.
At this point we would write the equation of motion, except that we wouldn't know theta0. Note that the omission of theta0 would be more serious for a University Physics than a College Physics student.
At t = 0 we know that x = .45 m so we have x = .45 m = .56 m * cos( omega * 0 + theta0) = .56 m * cos(theta0). Therefore
theta0 = arccos(.45 m / (.56 m) ) = arccos ( .80) = .64 rad, approx, or 2 pi - .64 = 5.64. At both of these angles we have x = .45 m; at x = .64 rad the velocity is in the negative x direction and at x = 5.64 rad the velocity is in the positive x direction.
Since both intial position and initial velocity are positive we conclude that theta0 = 5.64 rad.
The equation of motion is therefore approximately
The corresponding acceleration function is a = -(omega)^2 * A cos(omega t + theta0) or for the given situation
The position function is x = A cos(omega t + theta0). Substituting we obtain x = -.54 m.
At x = .54 m we have force
Alternatively using the acceleration and mass we have
Note that these results are consistent, which provides substantial confirmation that our model is correct.
a = F / m = 91 N / (.67 kg) = 136 m/s^2, approx., consistent with the acceleration found from the equations.
Problem Number 7If one Calorie of food energy is 1000 calories (note large and small c), and if one calorie is about 4.19 Joules of energy, and if your body is capable of converting about 15% of the food energy you consume into useful work, then if you used up all the energy in a 880-Calorie meal to power a special machine which would convert all your work into your kinetic energy, what speed could you attain (you may assume your own mass or, if you prefer, assume a mass of 66 Kg).
880 Calories is 880,000 calories or 880,000 * 4.19 J = 3,600,000 J approx..
15% of this is about 540,000 J.
A mass of 66 kg with KE = 540,000 J has velocity
v = sqrt( 2 KE / m) = sqrt( 2 * 540,000 J / (66 kg) ) = sqrt( (1,080,000 N m^2 / s^2 ) / (66 kg) ) = sqrt( 15,000 m^2/s^2) = 123 m/s, all calculations approximate.
Problem Number 8What are the components of the weight of a cart of mass 500 grams parallel and perpendicular to the 3.3 degree incline on which it rests?
The weight of a 500 gram cart is .5 kg * 9.8 m/s^2 = 4.9 N straight downward.
If the x axis is directed to the right and up the incline then the weight vector makes an angle of 270 deg - 3.3 deg = 266.7 deg with the positive x axis.
The components of the weight at therefore
wx = 4.9 N cos(266.7 deg) = -.3 N approx. and
wy = 4.9 N sin(266.7 deg) = 4.9 N approx.
Since only the weight and the normal force act in the y direction, and since there is 0 acceleration in the y direction, the normal force will be equal and opposite the y component of the weight.
.045 * Fnormal = .045 * 4.9 N = .2 N approx. so the frictional force, which opposes motion, will be +.2 N provided the cart is moving down the incline.
So the net force along the incline is -.3 N + .2 N = .1 N.
Your sketch should show the weight vector, the normal force perpendicular to the incline at almost as great as the weight. the weight component parallel to the incline much smaller than the weight vector, and the frictional force even smaller that the weight component along the incline and opposite to the direction of that vector.
Problem Number 9A simple harmonic oscillator is subjected to a net restoring force F = - 50 N/m * x at displacement x from equilibrium. It is observed to undergo simple harmonic motion with a frequency of 1.6 cycles / second. What is its mass?
We know that omega = sqrt(k/m).
The net force is F = - k x so k = 50 N/m.
Frequency is 1.6 cycles / sec and a cycle is 2 pi radians so omega = 1.6 * 2 pi rad/s = 3.2 pi rad/sec.
Solving omega = sqrt(k/m) for m we obtain
m = k / omega^2 = 50 N/m / ( 3.2 pi rad/s)^2 = .5 N s^2 / m = .5 kg.
Problem Number 10A cart of mass 1.4 kg is given an initial velocity of 2.4 m/s up a uniform incline at an angle of 5.4 degrees with horizontal. Assuming that the only forces acting on the cart are gravitational and normal forces, determine the following:
Assuming the incline is up and to the right the gravitational force component along the incline is 1.4 kg * 9.8 m/s^2 * cos(270 deg - 5.4 deg) = -1.3 N approx.
If the cart moves 1.24 m in the direction opposite to this force then the force does work
`dW = F `ds = -1.3 N * 1.24 m = -2.6 J approx..
The change in KE is equal to the work done by the net force acting on the system. Thus KE changes by -2.6 J.
The cart has initial KE of .5 m v0^2 = .5 * 1.4 kg * (2.4 m/s)^2 = 4 J approx.. Thus after the change of -2.6 J the KE will be 4 J + (-2.6 J) = 1.4 J.
Setting .5 m v^2 = KE we get v = sqrt( 2 * KE / m) = sqrt( 2 * 1.4 J / (1.4 kg) ) = sqrt( ( 2 kg m^2/s^2 ) / kg) = 1.4 m/s, approx..
The KE change is the work done on the cart; the work done by the cart is the negative of the work done on the cart so the KE change is the negative of the work done by the cart.
Force on the cart would have been in the same direction as displacement so KE would increase by 2.6 J, from 4 J to 6.6 J.
The resulting velocity would be v = sqrt( 2 KE / m ) = sqrt( 2 * 6.6 J / (1.4 kg) ) = 3 m/s, approx..
Problem Number 11
Coasting from rest down a certain hill, whose slope is variable, I reach a speed of 16.15 m/s at the bottom. If I coast from rest down the first half of the hill I reach a speed of 6 m/s. Ignoring the effects of air resistance and friction:
KE gain on entire hill = PE loss on entire hill = .5 M * (16.15 m/s)^2 = 130 M m^2/s^2, where M is my mass.
KE gain on first half = PE loss of first half = .5 M ( 6 m/s)^2 = 18 M m^2/s^2.
Thus PE loss on second half = PE loss on entire hill - PE loss on first half = 130 M m^2/s^2 - 18 M m^2/s^2 = 112 M m^2/s^2.
So KE gain on second half = 112 M m^2/s^2.
Starting from rest on the second half we would therefore attain velocity v such that
.5 M v^2 = 112 M m^2/s^2.
Solving for v we obtain
v = sqrt( 2 * 112 m^2 / s^2) = 15 m/s, approx..
PE loss on 2d half = M g h and PE loss on 2d half = 112 M m^2/s^2 so
M g h = 112 M m^2 / s^2 and
h = 112 m^2/s^2 / (9.8 m/s^2) = 11.4 meters.
Problem Number 12A simple harmonic oscillator is observed to undergo simple harmonic motion with a frequency of 1.8 cycles / second.
If the amplitude is A the maximum of acceleration is omega^2 * A and the max of velocity is omega * A. So for omega = 1.8 cycles / sec = 1.8 * 2 pi rad/s = 3.6 pi rad/s we have
Max acceleration occurs at the extreme points of motion at displacements x = + A and x = - A.
Max velocity occurs at the equilibrium point where x = 0.