Experiment 3 Questions and Comments

Question 1:  Plotting Quantity 2 vs. Quantity 1

I'm working on Experiment 3 and I'm not exactly sure what you are asking for regarding the first graph we are asked to construct.

• The instructions say to plot the average velocity on the second ramp vs. the average velocity on the first.
• I plotted my data for each ramp and made two separate lines.

Am I on the right track or not?

Answer:

As with the pendulum experiment, when you plotted period vs. length, you plot data points on a coordinate graph.

• When you plot Quantity 2 vs. Quantity 1, Quantity 2 goes on the vertical and the value of Quantity 1 on the horizontal axis.
• So your points would have 1st ramp velocity as the 'x' and 2d ramp velocity as the 'y' coordinate.

Question 2:  Plotting Quantity 2 vs. Quantity 1, Setup of Ramps

I have Physics 121, Experiment 3 underway but I don't know how to proceed with your assignment of plotting the average velocity on the second ramp vs. the average velocity on the first, for each distance on the first ramp.

• I think I'm supposed to do a calculation to combine the two numbers but I don't know what that is.
• I tried viewing the video clip which I think tells the answer, but ... from the clip I do think that the vertical line on the graph should be the centimeters of 10, 15...up to 50.
• One other problem I had was that the ball simply wouldn't complete the distance on the second ramp when I used the 10 cm. on the first ramp!
• Can I plot the others and ignore 10 cm?

Answer:

You can understand how to do the graph in terms of a table of data:

• Make a table of ramp 2 ave. vel. vs. ramp 1 ave. vel. (remember the conventions from the pendulum experiment: the ramp 1 vel. is the first, or 'x', column and the ramp 2 ave. vel. is the second, or 'y', column).
• Each data point on the table gives you the coordinates of a point on your graph.

As to your second question: 

• The second ramp is to be set up so that the ball maintains constant velocity on it--a ball given a slight nudge should keep going without speeding up or slowing down appreciably.  Therefore, if it comes off the first ramp with a velocity, it has to go the distance on  the second ramp.  It sounds like the second ramp needs a little more 'downhill' slope to maintain constant velocity.

Comment on Fitting a Straight Line to the Graph:

The graph below (and the table below the graph) represent ramp 2 ave. velocity vs. ramp 1 ave. velocity. 

The short black line is the best-fit line to the data. 

• The individual who did the experiment estimated uncertainties represented by the error bars.

• We see that the best-fit line has a slope of about 1.28 and a y-intercept of about 11.6.

• We also see that the best-fit line does not pass through all the 'error rectangles'--the rectangles defined by the error bars.

• The best-fit line does not agree with our expectation that the 2d ramp ave. vel. should be double that on the first. 

• If that was the case our line would be expected to have slope 2 and to pass through the origin.

• We plot the 'ideal' expected line in blue, thru the origin and with slope 2.

• We see that this line passes through the rectangle defined by the error bars of every point, so from this data we cannot rule out the hypothesis that this is the correct line. 
• In fact, this line fits the 'error rectangles' pretty well.

It is important to understand that any line that passes through all the rectangles defined by the error bars is a possible result of this experiment.

• Since the slope-2 line passes through all the rectangles, the slope-2 line is a possible result.  It's not the most likely, but it is possible.
• The slope-2 line doesn't fit the data points as well as the best-fit line, but it's pretty close to fitting the error rectangles as well as possible.
• You might try seeing what the range of possible slopes is, within the restriction of passing through the 'error rectangles'.  The range probably stays pretty close to 2.

Note that it is possible to underestimate error bounds, or to plot anomalous points, so that your data is inconsistent--i.e., so that no line goes through all the error rectangles.

• In this case the experimental results will not be valid, though you might still learn a lot from the experiment.

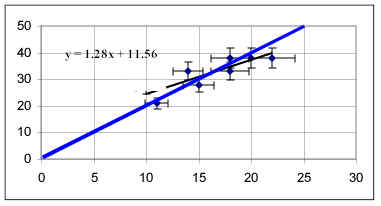
Table 2. Average Velocities for Ramps 1 and 2