Motion in 2 dimensions; Orbital Motion

Submit all results in the manner established for previous experiments.

Experiment 22. Motion in a force field: a computer simulation

This experiment consists of a simulation of an object moving in a force field.   The simulation depicts an object with an initial velocity which takes it into or near to a region with a force field whose direction is indicated by a grid of lines in the direction of the field. 

You are to predict the change in the speed of the object and the change in its direction of motion.

After running the simulation you should answer the following questions:

Experiment 23. The velocity of projectile is at every instant the resultant of its vertical and horizontal components.

Play the clip Prjctl01. You will see a projectile falling freely, with its motion stopped at uniform intervals of 1/30 second. You will trace its motion and determine its approximate x and y velocity chronicles, and its vector velocity chronicle. You will then determine whether the vector velocities are in fact the vector resultants of the x and y velocities.

Place a piece of clear plastic wrap over your entire computer screen, and prepared to make marks on the plastic with a dark permanent or non-premanent marker.

Superimpose your tracing on a piece of graph paper and collected the data you will need to determine x and y velocities, and vector velocities.

Determine the approximate x and y velocities observed for the ball.

Determine the distance moved during each time interval, and the direction of the motion.

Find the resultant of the x and y velocities at each midpoint clock time, and compare with the magnitude and angle just obtained.

Answer the following questions.

Experiment 24. The acceleration of an object moving in a circle at constant velocity is v^2 / r.

If we twirl a mass at the end of a light string of known length in a vertical circle, it is possible to adjust the speed of the spin so that at the top of the arc, the string just barely goes slack. At this instant the centripetal force holding the object in its circular path is just slightly less than the 9.8 m/s^2 acceleration of gravity. If the string is released at the instant it reaches its highest point, the object will at that instant become a projectile with a horizontal velocity equal to the velocity of the mass. From the initial height and subsequent horizontal range of the projectile, we will be able to determine the velocity of the mass at instant of release, when the centripetal acceleration of the system is 9.8 m/s^2.

By repeating the trial with a variety of different string lengths, we can find the proportionality between radius and velocity for a centripetal acceleration of 9.8 m/s^2.

Begin with a string length of 1 meter.

Repeat for string lengths of .8 m, .6 m, .4 m and .2 m and organize your results in a table of velocity vs. radius.

Compare your results to the derived result for centripetal acceleration.

There are at least 4 likely sources of error in this experiment, all of which are to at least some extent unavoidable when the experiment is run in the prescribed manner:

Speculate on the relative significance of the various unavoidable experimental errors.

Place bounds on the uncertainty in your determination of the horizontal range of the mass, and determine the resulting range of the values of 1/k in the above analysis.

Speculate on how we might design an experiment to minimize the errors that have occurred.

Experiment 25.   (a)  The effect of a force field on a projectile can be observed by rolling a steel ball past a magnet.  (b)  Change in orbital velocity with orbital radius can be modeled to a good approximation by projecting a rolling ball across a flat plane tilted at various angles so as to simulate gravitational acceleration.

(a)  The effect of a force field on a projectile can be observed by rolling a steel ball past a magnet.  You will use the large rectangular magnet and the steel ball, both of which were packed in your kit.

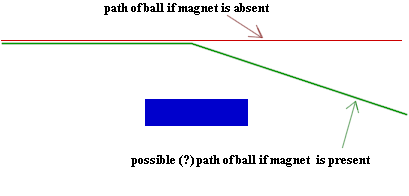
Roll a fast ball and a slow ball past the magnet with the initial path and orientation of the magnet as shown in the figure below, with each ball initially moving from left to right.  Roll the ball in a direction such that if the magnet is absent the ball will follow the straight-line path shown.  One ball should be rolled to that it gets past the magnet but is still visibly deflected, something like the indicated path below (we will soon ask the question of whether the path as indicated could be realistic).  The other should be rolled so it almost gets past the magnet but doesn't quite make it, and ends up stuck to the magnet.

Does the faster or slower ball get past the magnet?  Why do you think it is so?

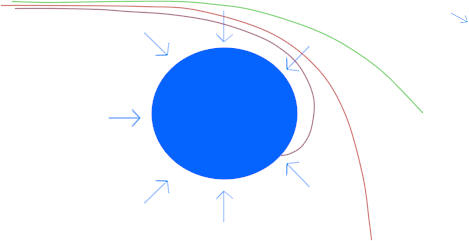
The field of the magnet is as shown in the next figure.  Note that the field drops rapidly as we move away from the magnet, and that the field is strongest near the center of the largest face of the magnet.  To the right and left of the magnet, as drawn below, the field is pretty weak and rapidly becomes insignificant as we move away from the magnet.

Given these characteristics of the force field:

 

Which of the paths shown in the figure below is more consistent with your previous answers?  Why?

The figure below shows a hypothetical circular disk magnet, which attracts steel objects equally around its entire circumference, and always toward its center.  It is not clearly indicated in the figure but again this field is to be regarded as decreasing rapidly as we move away from the disk. 

[  Note:  This is example depicts a magnetic monopole, a magnet with just a 'north' or just a 'south' pole without the opposite pole.  No magnetic monopole has ever been observed in nature (why a monopole has never been observed is unknown, and is one of the great mysteries of physics).  So nobody has ever created such an object and we are now in the realm of imagination.  ]

Three paths are shown below for a steel ball rolled past this hypothetical circular magnet, from left to right..

(b)  NOT CURRENTLY ASSIGNED:  A fairly small arc of a circle is sketched on a piece of paper and placed on a flat plane tilted in the x direction to simulate the acceleration of gravity in that direction, with the x direction coinciding with the axis of symmetry of the arc. The plane is tilted also in the y direction in such a way as to just compensate for the frictional resistance to a ball rolling across it in that direction. A curved-end ramp is used to give a steel ball a controlled initial speed and direction, and the speed and direction necessary for the ball to maintain a path at a (nearly) constant distance 'above' the arc are observed.

The tilt of the plane in the x direction can be adjusted to mimic the relative strengths of the gravitational field at various distances from the arc, and 'orbits' at these distances can be simulated.

Experiment 26. From a simulation we find that orbital velocity is inversely proportional to the square root of orbital radius; potential energy increase from one orbit to another is double the kinetic energy decrease so we have to speed up to slow down.

Click here for instructions using the former DOS version of the program, which is located under Simulations on the 'real' Physics I homepage.  This program should only be used if the program downloaded from the Sup Study ... site does not work.

Instructions for program grav_field_simulation.exe for Experiment 26:

The program will be found at the Sup Study ... site under Course Documents > Downloads > Physics I.   Download and/or run it in order to see the buttons and boxes described here:

The array of boxes and buttons at the right side of the screen contains information about the planet, the satellite and the time scale of the simulation.

Planet mass is the mass of the planet in multiples of the mass of the Earth. The default values assume that the planet is Earth, so the default planet mass is 1. You can enter any planet mass you wish. For example the Moon has a mass about 0.0123 times that of the Earth, the Sun has a mass which is about 340,000 times that of the Earth. If you wanted to simulate and orbit around the Sun or the Moon you would enter 0.0123 or 340,000 in this box.

Planet radius is given in multiples of the radius of the Earth. Since the default planet is Earth the planet radius has default value 1. If you wanted to simulate the Moon you might enter 0.26, which represents the fact that the Moon has a radius about 0.26 times that of the Earth. If you what and to simulate the Sun you might enter 1100, since the Sun has a radius about 1100 times that of the Earth.

Time factor is the factor but which the simulation is speed up. The default value of the time factor is 1,000, which means that everything runs about 1000 times faster than actual. This means, for example, that a low-Earth orbit will take place in about six seconds rather than the actual approximate time of 6,000 seconds.

Screen scale is the distance from the center of the picture to the edges, in Earth radii. The default value is 3, which works well for low and moderate Earth orbits. However if you are trying to investigate orbits which move further than 3 Earth radii from the center of the planet you need to adjust the screen scale accordingly or the satellite or projectile might not show up on the screen.

Initial distance is the distance of your satellite or projectile from the center of the Earth. This distance is set to 1.02, which is around the minimum distance at which it is possible to orbit at least a few times without encountering significant atmosphere. You can set it for any distance you wish. [ Note that this simulation ignores atmospheric drag and will work just fine for orbits inside the atmosphere. In fact it ignores any sort of interference at all so orbits low enough to encounter mountains will work just find here. Not only that, but this program implicitly assumes that all the mass of the planet is concentrated at its center and even allows orbits inside the surface of the planet. The only problem arises if you get very very close to the center of the planet, in which case the simulation breaks down and spits the satellite or projectile out at very high velocity in a straight line (which is just an anomaly of the simulation and would not really happen in any circumstance). ]

Initial angular position is the angle in radians made with the positive x axis (which is directed toward the right, as is standard for many applications) by a line segment from the center of the planet to the initial position of your satellite or projectile. Note that there are approximately six radians (actually 2 pi, closer to 6.28 radians) around a circle.

The impulse of the 'burn' is actually impulse per kg. Recall that the impulse of a force acting on an object, which is the product F `dt of the average force and time interval during which it acts, gives the change in the momentum of the object. It follows that the impulse kg is in fact the change in the velocity of the object. Note that we are here assuming that the 'burn' does not significantly change the mass of the object; this is not always the case with actual satellites and certainly is not the case with a rocket boosting a satellite into orbit. The default impulse is 8000, which will give the satellite or projectile a velocity of 8000 m/s, a bit in excess of the velocity required to achieve a circular low-Earth orbit.

To deliver an impulse you first choose the magnitude of the impulse, then click on the Forward, Backward, To Right or To Left button.

The direction of the initial impulse depends on the goal of the simulation. If we wish to achieve a circular orbit then because of the geometry of a circle (at every point the circle is perpendicular to the radial line from the center to that point) the impulse must be at a right angle to the initial angular position; otherwise circularity is in the first instant violated. Since a right angle is 1/4 of the angle around a circle, the right angle is 2 pi / 4 radians = pi / 2 radians, or approximately 1.57 radians. On the other hand if we wish to shoot a projectile 'straight up' from the surface of the Earth we must 'fire' it in the direction directly away from the center of the planet, which means that we must 'fire' along the radial line from the center to our starting point. This means that the initial direction must be the same as the initial angular position.

Clock time is displayed as the simulation runs. Clock time is the actual simulation time since the 'run' started.

Circle radius is the radius of a circular orbit you might be trying to achieve, in Earth radii.  If the number in this box is not zero then when you click Run Simulation the program will place a red circle of this radius, centered at the center of the planet, on the screen.

Realtime interval is the 'real world' time in minutes since the simulation began.

Speed is the speed of the satellite or projectile in meters/second.

The Run Simulation button is used to begin the simulation. When the simulation is begun the planet will show in blue the center of the screen and the satellite will show in white.

The first eight buttons in the rightmost column are used to deliver an impulse to the satellite or projectile.

The top four buttons deliver the impulse forward, i.e., in the direction of velocity of the object, or backward in the direction directly opposite that of the object's velocity, or to the right (defined to be at a right angle to the right as perceived by an individual facing the direction of motion) or to the left.

The default impulse is 0. The magnitude of the impulse is chosen by clicking one of the next four buttons. Once clicked this impulse is 'set' until another impulse button is clicked, so that it is possible with successive clicks to deliver any reasonable chosen impulse.

The Pause Simulation button, as you might expect, allows you to pause the simulation.  There are two reasons you might want to do this.   One is to simply have a look at the numbers in the boxes, another might be to change the numbers and restart the simulation without erasing the existing screen.

The Continue button will continue the program after a pause; if you haven't changed anything in the boxes the program simply picks up where it left off.

The Run (don't clear) button restarts the simulation after a pause, without erasing the existing screen.

 

The 2d planet button will create a second planet (e.g., the Moon), but first you have to go down to text boxes at the bottom of this column (just above the Apply button) and enter the necessary information. The default message in each box will tell you what you need to know, but those messages are repeated here.  Note that only the first word or two of each message actually shows in the box.

Be sure you have the correct numerical information in these boxes.  If you don't the program is likely to crash. 

After entering this information you can click on the 2d planet button, which will give you a message telling you that the 2d planet has been created. If the simulation is already running the second planet should appear, provided the screen scale can accommodate it. If not, or if you wish to make other changes, you may change the screen scale and any other information you wish then click on Run Simulation.

Suggestions for first-time use:

Without changing anything click on Run Simulation. You will see a blue circle representing the Earth and a moving white dot representing the successive positions of a satellite. The satellite completes its orbit 1000 times as fast as an actual satellite, due to the default time factor.

While the simulation is running click on 'Impulse 100' then on Forward and see what happens to the orbit.

Click on Forward a few more times and see what happens to the orbit.

Click on 'Impulse 1000' then on 'forward' and see what happens. Then click on 'right' and on 'left' and see what happens.

Any time the simulation gets out of control you can started over by clicking on Run Simulation. See if you can figure out the most efficient way to move from the default orbit into a 'higher' circular orbit. 

Do this: 

Start the simulation over:

Change the initial impulse:

Achieve circular orbits at 1.5 and 2 Earth radii:

Put the satellite into a circular orbit and investigate:

'Shoot' a projectile 'straight up' from the surface:  To shoot 'straight up' you shoot straight out along a radial line (see direction of the initial impulse in the description of the program above). 

 

 

The Experiment:

To start with you will determine the velocity required for a circular orbit at a distance of 1.2 Earth radii. 

Set Initial Distance at 1.2.  Leave the remaining settings as they are and click Run Simulation.

Determine from the shape of the resulting orbit whether the initial velocity is too high or too low and change the number in the Initial Velocity box to a value you believe will bring the orbit closer to a circular shape.  The click Run Simulation.

Repeat until you have achieved a good circular orbit and record the velocity.

Now find the velocity with which a projectile would have to be 'shot' from the surface of the Earth, ignoring air resistance, to get 'up' to the altitude of the orbit you have just created. 

Repeat but change your initial angular position to 1 radian (and of course change the initial direction of the 'shot' accordingly), and adjust your velocity to get closer to your goal.  Adjust the time of the simulation to allow the projectile to stop moving outward and begin falling back. Continue changing the intial angular position and your angular velocity until you manage to just reach the circular orbit you created in the first part of the experiment.

Repeat this procedure for the orbital radius you have been specifically assigned.

That is, determine the velocity necessary to maintain that orbit and the velocity required to achieve the altitude of that orbit.

If you have not been assigned an orbital radius use 1.2 + .1 * (number of letters in your first name).

Now achieve an elliptical orbit that just skims the surface of the Earth.

Starting from a position at 2 Earth radii from the center, adjust your initial velocity until you have an orbit that at its 'lowest' point just touches the Earth's surface.  Observe everything you can about the motion of the satellite in this orbit, including the maximum velocity.

Analysis

For each radius you investigated determine, by setting centripetal acceleration equal to gravitational acceleration, the 'actual' velocity for that circular orbit.

Compare with the velocities you obtained.

According to your observations:

According to theory:

For the elliptical orbit, based on your observations:

For the elliptical orbit, based on theory:

Speculate on what sorts of strategies are required to get a Space Shuttle into a circular orbit at an 'altitude' of 400 km.  Keep in mind that rocket fuel doesn't carry enough energy to even get its own mass into orbit.

Speculate on what strategies are required to get a spacecraft to the Moon, which is about 60 Earth radii away, and back.  Note that you can if you wish experiment with this situation by following the instructions for 2d Planet; just be careful to set your original parameters so that the Moon is visible.

Instructions for DOS program (ignore if you have performed the Windows version of this experiment)

We begin by determining the kinetic energy required to get from the surface of the Earth, at 1 Earth radius from the center of the planet, to 1.2 Earth radii, then to 1.4 Earth radii, then to 1.6, 1.8 and 2 Earth radii.

Your goal is to end up at a distance of 1.2 Earth radii from the center. Find the velocity that gets you as close as possible to that distance.

We now determine the velocity required for a circular orbit and orbital radii of 1, 1.2, 1.4, 1.6, 1.8 and 2 Earth radii.

Consider the proportionalities involved in energies and velocities.

We now consider the behavior of the satellite in an elliptical orbit.