class 050916

Write down the 4 equations of uniformly accelerated motion.  Time limit:  2 minutes.

Write down the definition of velocity and the definition of acceleration.  Time limit: 2 minutes.

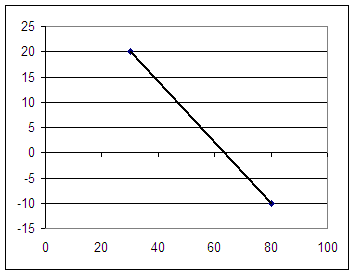
Find the slope and area beneath the following graph, and give the meaning and the units of the slope and the area

• if the graph represents velocity of an object in meters / second vs. clock time in seconds and
• if the graph represents the force exerted on an object in Newtons vs. the position of the object in meters

Solve the equation vf^2 = v0^2 + 2 a `ds for `ds.  Show your steps.

If you know v0, `dt and `ds, which of the four equations of uniformly accelerated motion will allow you to solve for vf?

Note the number of rubber bands you used for your slingshot, the number of dominos in the 'block' you projected.

Find force vs. pullback:

• Measure force vs. pullback for your rubber band system.  Get at least 4 readings over the range of your pullbacks.
• Graph force vs. pullback.  This graph will extend from pullback x = 0 to the maximum of all the pullbacks for which you measured the force.  For example if your maximum pullback was 10 cm, at which point your force was 3 N, then your graph would extend from 0 cm to 10 cm, and from 0 N to 3 N, including all forces and pullbacks as measured.

'Shoot' the block across the tabletop, keeping rotation to a minimum.  Use at least 4 different pullbacks.  Measure your pullbacks.

• Estimate as accurately as possible the force of every pullback you used.

Analysis for each trial:

• Sketch a rough graph of force vs. position for each trial.  Each graph will extend from the pullback position for that trial through the position when the block comes to rest.  For example if in your first trial the pullback was 4 cm and sliding distance was 20 cm past the unstretched position of the rubber band, the position might go from -4 cm to 20 cm.  Between -4 cm and 0 cm the rubber band force might decrease from .5 N to 0 N.  The rubber band force would then be zero from the 0 cm position to the 20 cm position.  You will sketch a graph of this type for each trial.
• Find the area beneath each graph corresponding to each trial.  This area will represent the work done by the rubber band.
• Make a table of sliding distance vs. area under graph.

You will get an area and a sliding distance for each trial.  Graph sliding distance vs. area under graph.

Read Chapter 2, and read through the problem set.

Problem assignments will be made next week and will include 6, 9, 11, 16, 22, 27, 37, 43, 52, 55, 58, 63 for Phy 201, all Level I problems for Phy 121.

How do I make a rough estimate, for a typical suburban house, of the % of its outside wall area that consists of window area? It is question 30 in chapter 1

<h3>One way would be to make a sketch of a typical side of a typical house, then measure the dimensions of the side and the dimensions of the windows. Figure out the areas.

Quicker and just as good: Make your sketch. Then try to fill the rest of the wall with average-sized windows and see how many windows it takes, compared to how many you originally had in your sketch.</h3>

How do I make a rough estimate, for a typical suburban house, of the % of its outside wall area that consists of window area? It is question 30 in chapter 1

One way would be to make a sketch of a typical side of a typical house, then measure the dimensions of the side and the dimensions of the windows. Figure out the areas.

Quicker and just as good: Make your sketch. Then try to fill the rest of the wall with average-sized windows and see how many windows it takes, compared to how many you originally had in your sketch.

What do you sub in for x (distance traveled) when you are trying to find out if the equation will work?

I'm sorry but I not sure which equation you are talking about. Can you clarify?

What is the definition of work? I had in my notes work=avg.force*change in position, today you said that work=avg.force*'ds.

'ds=avg.velocity*'dt, I didn't think that 'ds and change in position were the same.

<h3>Good question.

For clarification, `ds is change in position.

ave vel =
ave rate of change of position with respect to clock time =
change in position / change in clock time =
`ds / `dt.

`ds is change in position.</h3>

<h3>Do them and come to class with the problems done, because there's a good chance you'll need to repeat part of your explanation of a problem on a quiz.</h3>

A question I have is, the Force constant is the avg. altitude of the forces on a force vs. position graph. So what does that
mean, other than the constant force that is being applied? Is it like the acceleration, being a measure of the consistency of
velocity. But the force constant being the consistency of the application of force?

<h3>The force constant is represented by the slope of the graph of force vs. position. This means that the force constant is
the rate of change of force with respect to position.

The average altitude of a force vs. position graph represents the average force.

We talk about a 'force constant' when the slope of the force vs. position graph is constant. Note that force vs. position
does not generally have a constant value for a rubber band, but it does for the bungee cord we used in the preceding class.

Note again that a force constant is the rate of change of force with respect to position. When the force constant is really
constant (e.g., the 6.2 Newtons / foot measured in class) then if you multiply change in position by force constant, you get
the change in force.

So for example if I stretch the bungee cord by an addition 2 feet, at 6.2 Newtons / foot, the force will increase by 12.4
Newtons.</h3>

Secondly, When you were using the scale to see how many newtons were put into the system, you said the number of newtons *
9.8. Was the 9.8 the acceleration of gravity? Thank you,

</h3>The scale I was using measures kilograms. Kilograms are not units of force, but units of mass. The scale is designed
to hang objects from, and it reads their mass in kilograms, assuming that it is Earth's gravitational field that pulls them
down.

A mass of 1 kilogram near the surface of the Earth experiences a force of 9.8 Newtons as a result of Earth's gravitational
field.</h3>

When you ask to write the correct number of significant fiqures for 2.35 * 10^4 are you asking for the answer 23,500
 

<h3>The number of significant figures in 2.35 * 10^4 is three. The 2, the 3 and the 5 are significant figures. When you
write 23,500 the 2, 3 and 5 are again significant figures but the two zero's are not.

2.35 * 10^4 implies that the quantity was observed to 3 significant figures, and that only these three figures are
significant.

Had the quantity been reported as 2.350 * 10^4, then the 0 would be considered significant. There is no good way to signify
this with the form 23,500 so in this case only the scientific notation would tells you the number of significant figures.

2.3500 * 10^4 would indicate that both zeros are significant, and the expanded number could be written 23,500. with the . at
the end indicating that everything up to that point is significant.</h3>

I already graphed my data, and looked over the 4 equations, is this all we had to do?

I think that puts you in good shape, if by 'looked over' you mean 'branded into your memory so you'll never forget', 'understand the derivation of', 'know how to use' and 'know how to solve for any variable'.

My guess is that being a demonstrably hard-working student, you're well on your way to these goals. We'll try to move you even further along tomorrow.

What is the quadratic formula?

The quadratic formula tells you that a t^2 + b t + c = 0 if, and only if, t = [ -b +- sqrt(b^2 - 4 a c) ] / ( 2 a ).

You would apply the formula to solve the equation

`ds = v0 `dt + 1/2 a `dt^2

for `dt, as follows:

Rearrange the equation to the form

1/2 a `dt^2 + v0 `dt - `ds = 0.

substitute your values of a, v0 and `ds.

Whatever quantity you end up with in front of `dt^2 takes the role of a in the quadratic formula, not to be confused with the acceleration a (even though in this case the two are related).

Whatever quantity ends up in front of `dt takes the role of b.

Whatever - `ds happens to be, that's c.

Plug those numbers into the formula. Depending on the value of the discriminant, which is the b^2 - 4 a c quantity within the square root, you will get no solution (if b^2 - 4 a c is negative you can't take the square root), 1 solution (if b^2 - 4 a c = 0 then the + and the - of the +- give you the same thing) or 2 solutions (if b^2 - 4 a c is positive then its square root is real and nonzero, so you will get a solution for the + and a solution for the - of the +-).

If you get no solutions, then that combination of `ds, v0 and a is not possible.

If you get 1 or 2 solutions, then you have to decide which, if any, actually fit the problem.

As I said in class, you generally avoid solutions that require the quadratic formula unless you are left with no choice. In Phy 231 and 241, this happens frequently; in 201 is happens but only on a few problems in the entire course; in 121 it's not something you have to worry about.

In any situation where you have a, v0 and `ds you can instead use the fourth equation vf^2 = v0^2 + 2 a `ds to solve for vf, then you can just use straightforward reasoning to find `dt.


What is the definition of work? I had in my notes work=avg.force*change in position, today you said that work=avg.force*'ds.
'ds=avg.velocity*'dt, I didn't think that 'ds and change in position were the same.

Good question.

For clarification, `ds is change in position.

ave vel =
ave rate of change of position with respect to clock time =
change in position / change in clock time =
`ds / `dt.

`ds is change in position.