0830 Quiz

1.  If between clock times t = 5 sec and t = 15 sec an object travels from position 12 cm along a meter stick to position 80 cm then

• What is the object's average velocity?

Ave vel = ave rate of change of position = change in position / change in clock time = (80 cm - 12 cm) / (15 sec - 5 sec) = 68 cm / (10 sec) = 6.8 cm/s.

• If the velocity of this object changes at a uniform rate, starting from rest, then what is its final velocity?

Common response is that the final velocity is 6.8 cm/s.  If we take this response to the next step, we conclude that the average of initial and final velocities is the average of 0 cm/s and 6.8 cm/s, which is 3.4 cm/s.

However a graph of v vs. t is a straight line, since velocity changes at a constant rate.  So the average velocity occurs at the midpoint of the line segment representing this time interval, and for a straight-line graph the midpoint value is the average value.

We would conclude that the midpoint value is 6.8 cm/s from the given information, but that it must be 3.4 cm/s from the common response given here.

Cain't be both.

How to fix the conclusion?

What must be averaged with the initial velocity 0 cm/s to get the average velocity 6.8 cm/s?

Must be 13.6 cm/s, since (0 cm/s + 13.6 cm/s) / 2 = 6.8 cm/s.

Don't confuse final velocity with average velocity. 

• Final velocity is the velocity you end up with. 
• Average velocity is what you multiply by the time interval to get the displacement.

• Show whether the average velocity of the object equal to the average of its initial and final velocities.

If we answered the previous question correctly this will be true, since rate of change of velocity (i.e., acceleration) is uniform.

Note that this won't necessarily be the case if acceleration is not uniform.

If the graph above represents the expected number of really stupid things in any given day I would do at different ages:

• At what age would I have been expected to do the greatest number of stupid things in a day? 

• At what other age or ages did I experience relative peaks in frequency of stupid actions? 

• Over what age ranges was I apparently getting stupider?

• Over what age ranges was I apparently getting lesser stupider?

• At what age did stupidity appear to be increasing fastest? 

• At what age did stupidity appear to be increasing most slowly?

• How many stupid things does it look like I did during the third decade of my life so far? 

The third decade runs from age 20 to age 30.  The maximum number of stupid things per day looks like it occurred at age 20, and was around 85 stupid things / day.  The minimum number appears to be in late 20's where i was doing around 45 stupid things / day.  The average of these two rates is about 65 stupid things / day. 

Over the 10-year period, in which there were about 3650 days, this gives over 200,000 stupid things.

• How many stupid things does it look like I did during the decade when I did the most stupid things? 

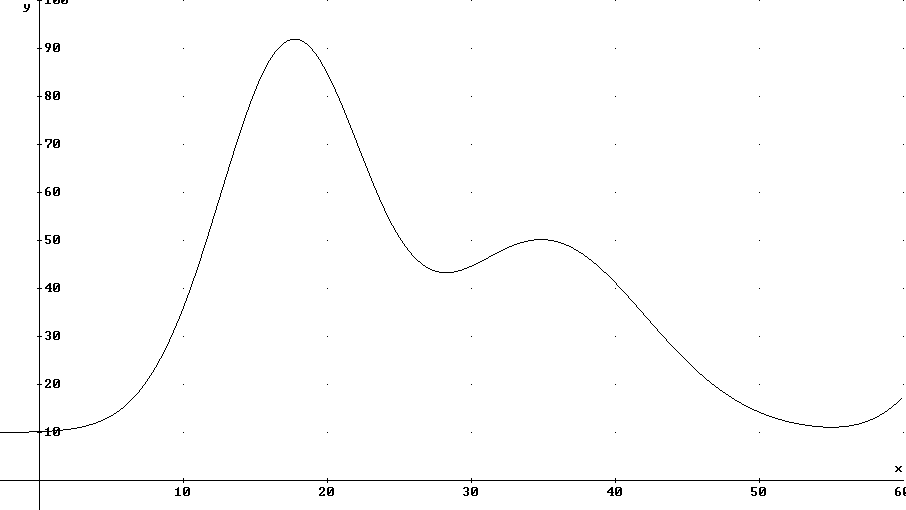
If this graph represents the velocity in cm / s of a marble rolling down a long, undulating incline vs. clock time in seconds then

• At what clock time is the velocity greatest?

• At what clock time is the velocity least?

• If the marble traveled at its greatest velocity for the entire 60 seconds how far would it travel

Greatest velocity is about 90 cm/s.  In 60 sec the displacement would be (90 cm/s) * 60 s = 5400 cm, approx., or about 54 meters.

• If the marble traveled at its least velocity for the entire 60 seconds how far would it travel?

Least velocity is about 10 cm/s, which in 60 sec would give you a distance of 10 cm/s * 60 s = 600 cm, or about 6 meters.

• At what clock time is the velocity increasing most rapidly?

Velocity appears to be increasing most rapidly at around t = 14 sec, where the graph is steepest.

This is the point at which the rate of change of velocity with respect to clock time, i.e., acceleration, takes its greatest value.

• Approximately how far does the marble roll between t = 30 sec and t = 40 sec?

'How far' can be identified here with change in position.

ave vel = change in position / change in clock time.

So

change in position = ave vel * change in clock time.

We use ave vel, not change in vel, not final vel, not initial vel, not our favorite vel.

Eyeballing the interval we see that the velocity ranges from around 40 cm/s to around 50 cm/s, probably averaging a little close to 40 cm/s.  Let's estimate the average velocity on this interval as 44 cm/s.

We get

• change in position = ave vel * change in clock time = 44 cm/s * 10 s = 440 cm.

On the graph the 44 cm/s represents the average altitude of the graph and the 10 s represents the width of the graph region beneath the curve.  The area of the rectangle with altitude 44 cm/s and width 10 s is  ht * width = 44 cm/s * 10 s = 440 cm.

The area beneath the curve of a v vs. t graph corresponding to a given time interval is the displacement that will occur during that interval.

Univ Phy:  The area beneath the curve for an interval is the definite integral of the function over that interval.

• Approximately what is the marble's greatest acceleration?

Intuitively you will probably say that the acceleration is greatest around t = 14 sec, which is where the graph is steepest.  This is correct.  In detail:

Average acceleration is average rate of change of velocity with respect to clock time.

Average rate of change of velocity with respect to clock time is change in velocity / change in clock time.

On the graph change in velocity is represented by the rise between two points, and change in clock time by the run.

So the average acceleration between two points on a v vs. t graph is represented by rise / run = slope.

Sketching a line whose slope matches the maximum slope we can then find two points on that line and find its slope.  The two points we get are (6s, 0 cm/s) and (13 s, 80 cm/s), giving us a slope of (80 cm/s - 0 cm/s) / (13 s - 6 s) = 80 cm/s / (7s) = 11.4 (cm/s) / s approx..

• Make a reasonable estimate of the average velocity for the 60-second interval.

A straight horizontal line at about v = 37 cm appears to about split the area of the graph into equal regions above and below the line, so 37 cm is a decent estimate of the average velocity, off by perhaps +- 2 cm/s.

So a reasonable estimate of the total distance might be 37 cm/s * 60 s = 2220 cm, about 22 meters.

• Make a reasonable estimate of the length of the track.

• Describe a possible track which would result in this velocity vs. clock time graph.

If this graph represents the position in cm of a marble rolling down a long, undulating incline vs. clock time in seconds then

• At what clock time is the velocity greatest?

• At what clock time is the velocity least?

• At what clock time is the speed greatest?

• At what clock time is the speed least?

• If the marble traveled at its greatest velocity for the entire 60 seconds how far would it travel?

• If the marble traveled at its least velocity for the entire 60 seconds how far would it travel?

• At what clock time is the velocity increasing most rapidly?

• At what clock time is the velocity decreasing most rapidly?

• Approximately how far does the marble roll between t = 20 sec and t = 30 sec?

• Approximately what is the marble's greatest acceleration?

• Make a reasonable estimate of the average velocity for the 60-second interval.

• Make a reasonable estimate of the length of the track.