0903 Quiz
The answers to questions 1-3 should be clear from previous notes, and will not be included in this document. Refer to previous class notes if necessary.
1. Give the definition of velocity and the definition of acceleration.
2. From a graph of velocity vs. clock time,
- How do you get the average velocity between two given clock times?
- How do you get the displacement between two given clock times?
3. Given a graph of position vs. clock time, what is the meaning of each of the following and explain in detail how you reason out your answers:
- The slope between two points.
- The area beneath the curve between two points.
4. Given a graph of acceleration vs. clock time, what is the meaning of each of the following and explain in detail how you reason out your answers:
Slope = rise / run = change in acceleration / change in clock time = average rate at which acceleration changes with respect to clock time
For a straight-line graph the average acceleration will be the midpoint acceleration and change in clock time will be the width of the region.
So when we multiply average 'height' by width to get the area, we are multiplying average acceleration by change in clock time.
Ave. accel. = ave rate of change of velocity with respect to clock time = change in velocity / change in clock time.
In shorthand symbolic notation:
We just found that the area beneath the curve is aAve * `dt.
Since aAve = `dv / `dt, we know that aAve * `dt = `dv.
So the area beneath our curve is change in velocity.
5. Given a graph of one quantity vs. another, what questions do you ask in order to interpret the graph?
You should have listed a good representation of the questions you were given last time to memorize. See the 'stuff to be memorized' link under the link to Fall 04 class notes (bottom of Assts page).
6. If a graph of velocity vs. clock time is increasing then what can you conclude?
If the graph is increasing then its slope is always positive, meaning that the acceleration is always positive.
This is the case whether velocity is negative or positive (e.g., negative velocity and positive acceleration means you're slowing down, positive velocity and positive acceleration means you're speeding up).
7. If a graph of position vs. clock time is increasing then what can you conclude about the velocity vs. clock time graph?
The slope of the position vs. clock time graph is velocity. If the graph is increasing then slope is positive, meaning that velocity is positive.
8. If velocity is increasing then what can you conclude about the position vs. clock time graph?
On a position vs. clock time graph, velocity is represented by slope. So if velocity is increasing, the slope of the position vs. clock time graph is increasing.
9. Suppose that velocity increases from v0 to vf while clock time increases from t0 to t1. If the graph is linear then
On a graph of v vs. t, if the graph is linear (i.e., if acceleration is uniform) the average velocity is the midpoint velocity, by symmetry. The midpoint velocity will be the average of the initial and final velocities so
vAve = (vf + v0) / 2.The change in velocity is final velocity - initial velocity = vf - v0 so
Acceleration is ave rate of change of velocity = change in velocity / change in clock time so
a = `dv / `dt = (vf - v0) / (tf - t0).Displacement is vAve * `dt; since vAve = (vf + v0) / 2 and `dt = tf - t0 we have
We have obtained the two equation `ds = (vf + v0) / 2 * `dt and a = (vf - v0) / `dt. Rearranging the second and keeping the first as it is we get the first two equations of uniformly accelerated motion:
These equations involve the five quantities `ds, `dt, v0, vf and a. Given any three of these five quantities the two equations give us a set of two simultaneous equations for two unknowns, so we could solve to find the remaining two of the five quantities.
If we eliminate vf from the two equations (substitue v0 + a `dt into the first equation in place of vf) we get the equation
If we eliminate `dt from the two equations we get the equation
This gives us a set of four equations in the five quantites `ds, `dt, v0, vf and a:
Given any three of the quantities `ds, `dt, v0, vf and a we can find an equation containing these three quantities and can therefore solve for the fourth. Then we will have four quantities, three of which can be substituted into one of the other equations to find the fifth.

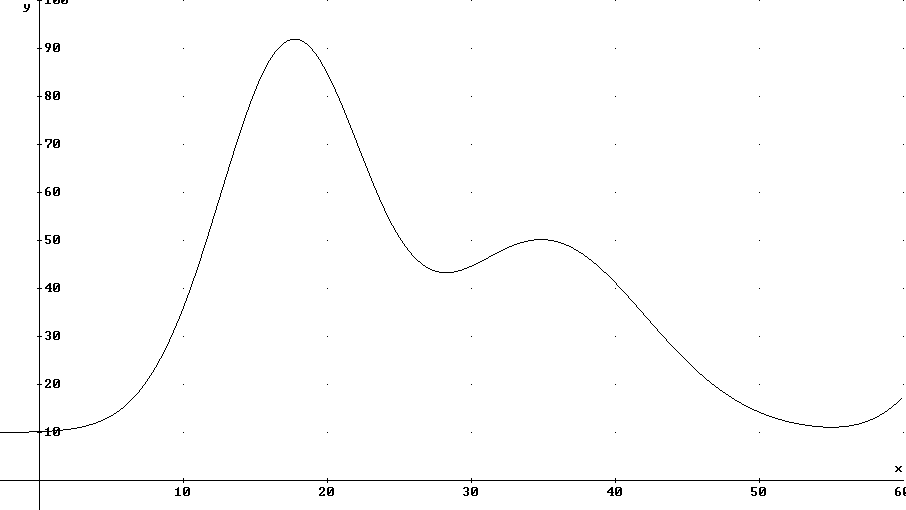
If this graph represents the position in cm of a marble rolling down a long, undulating incline vs. clock time in seconds then