Class 0908

Note that directions for the practice/quiz program are given at the end of this page.

0908 Quiz

1. On inclines of 3%, 5% and 8% it is observed that a cart rolls from rest down the incline in time intervals, repectively, of 6.7 sec, 4.2 sec and 3.6 sec. The length of each incline is 1300 cm.

Find from the given information the average velocity, final velocity and change in velocity on each incline.
Find the acceleration on each incline.

On the first incline:

The average velocity is 1300 cm / (6.7 sec) = 195 cm/s, approx..

On a straight incline acceleration is uniform, so a graph of v vs. t would therefore be a straight line segment starting at v = 0, with average v coordinate 195 cm/s. The final velocity would therefore be 390 cm/s.

Change in velocity is (390 cm/s - 0 cm/s) = 390 cm/s. So acceleration is

a = `dv / `dt = 390 cm/s / (6.7 s) = 58 cm/s^2.

Similar calculations apply to the other two inclines. The table below summarizes the results:

% incline `dt vAve vf a

3% 6.7 194.0 388.06 57.92

5% 4.2 309.5 619.05 147.40

8% 3.6 361.1 722.22 200.62

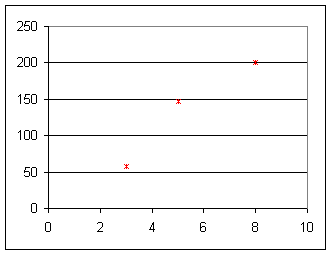
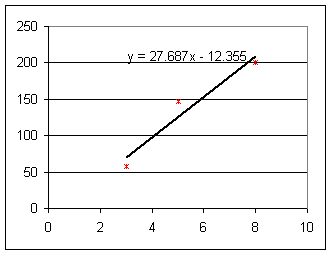
2. Using the information you obtained in #1, sketch a graph of acceleration vs. percent incline. Find the slope of this graph, and give the meaning of the slope.

A table of acceleration vs. % incline gives us:

% incline	a
3%	57.92
5%	147.40
8%	200.62

giving us the graph of acceleration in cm/s^2 vs. percent incline:

Estimating the slope of a decent straight line we might get rise = 230 cm/s^2, run = 9% so slope is about

slope = 230 cm/s^2 / (9%) = 25 cm/s^2 / (% unit).

3. On the first of the inclines in #1, of the quantities v0, vf, `dt, a and `ds, which were you given?

We were given v0, `dt and `ds, the initial velocity, time interval and displacement.

Which of the equations `ds = (v0 + vf) / 2 * `dt, vf = v0 + a `dt, `ds = v0 `dt + .5 a `dt^2 and vf^2 = v0^2 + 2 a `ds contains all three of the quantities you were given, and what quantity is unknown?

The first equation contains all the quantities except vf, so could be used to find vf.

The second equation is missing vf and a. If vf was first found using the first equation we could then use the second equation to find a.

The third equation contains all the variables except a and could therefore be used to find a directly, without having to go through two equations to get there.

The fourth equation is missing vf and a. There would be no reason to use this equation.

Solve that equation for the unknown quantity and substitute the values of the known quantites to find the value of this fourth quantity.

Using the first equation `ds = (vf + v0) / 2 * `dt we solve for vf.

First we multiply both sides by 2 / `dt to get

2 `ds / `dt = vf + v0. Then we subtract v0 from both sides to get

vf = 2 `ds / `dt - v0. Substituting v0 = 0, `ds = 1300 cm and `dt = 6.7 sec we get

vf = 2 * 1300 cm / (6.7 sec) - 0 cm/s = 390 cm/s, approx..

Find an equation which includes the one quantity of the original five which you do not yet know. Solve that equation for this unknown quantity, the substitute the values of the known quantities to find the value of this fifth quantity.

The equation `ds = v0 `dt + 1/2 a `dt^2 contains the three quantities we were given and the remaining unknown a.

To solve for a we first subtract v0 `dt from both sides to get

`ds - v0 `dt = 1/2 a `dt^2. Then multiply both sides by 2 / `dt^2 to get

a = 2 ( `ds - v0 `dt) / `dt^2.

Substituting the known quantities we get

a = 2 ( 1300 cm - 0 * (6.7 sec) ) / (6.7 sec)^2 = 58 cm/s^2.

This doesn't answer the question but note anyway:

The second equation vf = v0 + a `dt could now be used to find a:

Subtracting v0 from both sides we get

vf - v0 = a `dt. Dividing both sides by `dt gives us

a = (vf - v0) / `dt (which of course is something we knew anyway). So

a = (390 cm/s) / (6.7 sec) = 58 cm/s^2, approx..

What do you conclude is the average velocity on this incline?

What do you conclude is the average acceleration on this incline?

4. For the graph given below answer the questions that follow.

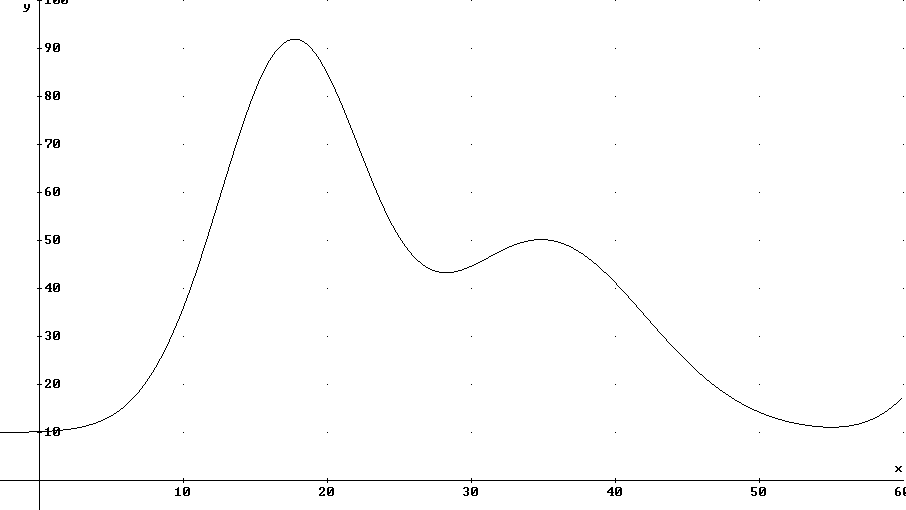
If this graph represents the position in cm of a marble rolling down a long, undulating incline vs. clock time in seconds then

At what clock time is the velocity greatest?

At what clock time is the velocity least?

At what clock time is the speed greatest?

At what clock time is the speed least?

If the marble traveled at its greatest velocity for the entire 60 seconds how far would it travel?

If the marble traveled at its least velocity for the entire 60 seconds how far would it travel?

At what clock time is the velocity increasing most rapidly?

At what clock time is the velocity decreasing most rapidly?

Approximately how far does the marble roll between t = 20 sec and t = 30 sec?

Approximately what is the marble's greatest acceleration?

Make a reasonable estimate of the average velocity for the 60-second interval.

Make a reasonable estimate of the length of the track.

5. Sketch a graph of velocity vs. clock time for this marble.

Directions for Practice/Quiz Program.

This program is easy to use, once you've been through the process once.

If you are working at home you need only go through the download process once, and it's only a 1-step process to run the program.

If you are working from VHCC you might have to go through the process each time you use the program, but it only takes a couple of minutes once you know what to do. Once the network is properly set up there will be a version that runs much more conveniently from the LAN.

Go to Web address www.bb.vccs.edu and log in. If you don't yet have your login name you can log in as vhstudent with password college.
Go to Supervised Study Current Semester (NOT to your Physics page) and Click on Course Documents.
At the top of the page is the program VBRUN60. Run it (just one time) to be sure your computer is set up to run VB programs. This is not necessary on VHCC computers.
Just below that is the program q_a_prelim. Run it and as soon as it pops up, close it. This program will create a folder entitled c:\vhmthphy on your hard drive. Alternatively, if you prefer, you can create this file yourself. If you are working on VHCC computers you will probably need to do this each time your run the program.
Scroll down that page until you see Multiple Choice Generating Program. Either run the program or copy it to your desktop or some other location on your computer. However don't answer any questions yet.
Just above that program on your Blackboard page you will find a link entitled Downloads. Click on that link, then scroll down until you find the name of your course and click on that link.
At the bottom of the page for your course you will find the file 201_c.txt. Right-click on that file, choose Save Target As..., browse your way into the folder C:\vhmthphy and save the program, without changing the name of the program.
Return to the Multiple Choice Generating Program. Enter your VHCC username in the box where it is requested.
A form will pop up. Click on the Menu button.
Enter 201 for your course number.
A list of topics will appear. Enter the number of your choice.
Wait until a message pops up telling you how many questions you will have and OK that box.
The next box allows you to choose whether the questions will have just 1 correct answer or may have multiple correct answers.
Once you have answered this box the screen will tell you to click on the 'next question' button. When you do a question will pop up.
Next you click on the Display Choices button and your choices will pop up.
Once you have decided which choice or choices are true you can click on the Answer Questions button. Enter the letter(s) corresponding to the valid choice(s).
Click on the See Results button, which will give you (often repetitive) feedback on each of your answers.
Click on the Next Question button and repeat the process.

If you're working at home, once the 201_c.txt file is in the c:\vhmthphy folder and the program itself is on your desktop, you just need to double-click to run the program.

It will be equally easy at VHCC once the network is set up to accomodate the program.

% incline	`dt	vAve	vf	a
3%	6.7	194.0	388.06	57.92
5%	4.2	309.5	619.05	147.40
8%	3.6	361.1	722.22	200.62