1022

• Run Multiple Choice Generator at h:\shares\physics
• Run Core Problems by giving the program qzz as your 'course'--enter this when asked for your 3-digit course number.   Do the Physics Quiz 1022.
• If you miss a problem be sure to click on Comment and explain what you do and do not understand about the question and the given solution

University Physics students note:  instructions_for_program_on_basic_calculus

Graph PE vs. position for pendulum.

If PE increases as you move away from the equilibrium position then the equilbrium is stable.

 Think of a pendulum at equilibrium.  If you push it to the right or left, the horizontal component of the tension in the pendulum string tends to move it back toward the equilibrium position.  So the tension force is opposing your attempt to move it away from equilibrium.  As the pendulum moves to the right or left its vertical position increases, which increases it gravitational PE.

If PE decreases as you move away from the equilibrium position then the equilbrium is unstable.  A meter stick standing on its end will lose PE as you move it away from the equilibrium position.

Systems tend to fall into 'low points' of PE vs. position graphs, and away from 'high points'.

A stick constrained to rotate in a vertical circle about one of its ends illustrates both stable and unstable equilibrium.  When hanging straight down the stick is in its lowest position; any rotation right or left raises it a bit, thereby increasing its gravitational PE, so the stick is at a point of stable equilibrium.  When at the top of its arc any rotation to the right or left will lower the stick and decrease its gravitational PE, so this is a point of unstable equilibrium; the stick could be balanced at this point, at least theoretically, but the smallest nudge to right or left causes it to fall toward its position of stable equilibrium.

The bottom of the hill on a roller coaster is a point of stable equibrium, the top of a hill is a point of unstable equilibrium.  A roller coaster system typically has multiple points of stable and unstable equilibrium.  As it moves toward a point of stable equilibrium its PE increases, and as it moves toward a point of unstable equilibrium its PE decreases.

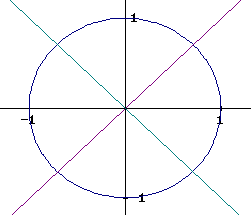
Sines and Cosines

Angles are always measured from the positive x axis.

Draw a unit circle with the origin at the center.

For any angle theta find the point where the radial line intersects the circle.

sin(theta) is the y coordinate of that point

cos(theta) is the x coordinate of that point

You should be able to visually estimate within +-.1 the sine or cosine of any given angle.

You should be able to estimate within +-5 degrees the angle corresponding to any point on a unit circle.

You should then be able to use your calculator to check your visual estimates of the sine and the cosine.

You should finally be able to check the plausibility of your sine and cosine estimates by checking whether sin^2(theta) + cos^2(theta) is close to 1.  For any angle, sin^2(theta) + cos^2(theta) = 1 by the Pythagorean Theorem.

Note the following behaviors of the sine and cosine:

As we move a little ways from 90 degrees or from 270 degrees the sine changes very little, the cosine changes almost in proportion to how far we move.

As we move a little ways from 0 degrees or from 180 degrees the cosine changes very little, the sine changes almost in proportion to how far we move.

Applications of Vectors

• Pendulum

For small angles:

• Ty is close to T because sin(theta) is close to 1
• Very little vertical acceleration so Ty is close to mg (vertical equilibrum, nearly)
• So T is close to mg.
• Therefore Tx is close to m g cos(theta).

From a picture of the situation we easily figure out that cos(theta) = -x / L.

• Therefore Tx = m g * ( -x / L).

This is the net force on a free pendulum (small-angle approximation).

Thus

• Fnet = m g ( -x / L) or
• Fnet = -(m g / L) * x.

This is of the form

• Fnet = - k x

where k is a constant.

• Forces on Incline

We place the x axis along the incline.  The weight vector is vertical, the friction vector f is along the incline opposed to the direction of motion, the normal force F_normal is perpendicular to the incline.

For an 8 degree incline, up and to the right, the angle of the weight vector is 270 deg - 8 deg = 262 deg.  So the weight vector breaks into x and y components

• wt_x = m g * cos(262 deg) = -.14 m g   and
• wt_y = m g * sin(262 deg) = -.99 m g.

There are no other forces.  Assuming equilibrium,

• f + -.14 m g = 0  ( x equilibrium)
• F_normal + -.99 m g = 0 (y equil).

Solving for f and F_normal we get

• f = .14 m g
• F_normal = .99 m g.

• Pulling at non-horizontal angle on cart

We have equilibrium in the y direction so we put the x axis in the horizontal direction, with the pull at 30 degrees.

If we pull with a force F at angle 30 deg above horizontal, then we get

• F_x = F cos(30 deg) = .87 F and
• F_y = F sin(30 deg) = .50 F.

The frictional force f, the weight force - m g and the normal force F_normal then give us

• F_xNet = f + .87 F
• F_yNet =

  F_normal + .50 F - m g

We have y equilibrium so

• F_normal + .50 F - m g = 0

which we solve to get

• F_normal = m g - .50 F.

We don't necessarily have x equilibrium, depending on the coefficient of friction.

frictional force f can be as great as `mu * F_normal, and will be equal to this quantity if the cart moves.

`mu is the coefficient of friction.  For the cart assume `mu = .15.  So the frictional force can be as much as .15 times the normal force.

For the given quantities, F = 100 N and weight = 25 kg * 9.8 m/s^2 = 490 N.

• Projectiles with Nonzero Initial Vertical Velocity

Impulse-Momentum