1103
Experiment:
Roll a ball down a ramp which is inclined by a single marble block so that it rolls to the end of the ramp, then drops to the edge of the table and rolls off. Based on its projectile behavior determine its velocity. Note also the specific position where the ball strikes the floor so that you can determine deviations from the direction of the ball's path as well as deviations in its speed.
Position a magnet so that the main field of the magnet is perpendicular to the path of the ball, 6 cm away from the path of the ball's center.
Roll the ball down the ramp so that it passes the magnet before rolling off the edge of the table.
See if there is any change in the direction of the ball's motion.
From your information on the exact spot at which the ball hits the floor, determine the change in the ball's velocity perpendicular to its original path.
Determine also if the speed of the ball.changed due to the presence of the magnet.
Repeat with the magnet 5 cm from the path.
Repeat again with the magnet 4 cm from the path, then 3 cm, then 2 cm, then 1 cm. If the ball doesn't make it off the table, note that also, and don't bother with any closer distances.
Repeat the entire procedure again with the ball rolling down only half the ramp.
For each run the experiment:
Determine how long it took the ball to travel a distance equal to the length of the magnet.
From the change in the ball's momentum, determine the average force exerted by the magnet during this interval, assuming that 90% of the momentum change occurred during this interval.
Plot the average force exerted by the magnet vs. the ball's distance from the magnet.
See if it is possible with the right combination of ball speed and magnet placement to have the ball end up stuck to the 'back' pole of the magnet--i.e., to the pole on the side of the magnet which doesn't face the path of the ball.
*************
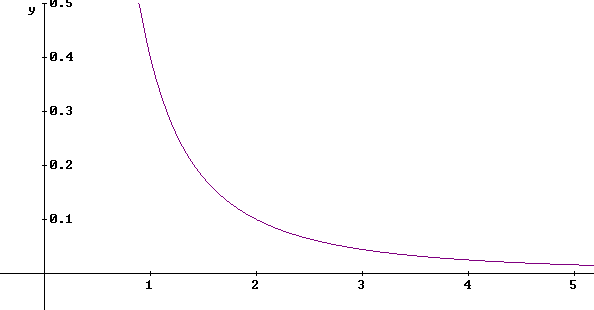
The graph below depicts magnitude of the force exerted on a certain ball by a magnet vs. the distance between ball and magnet. Force is in Newtons while distance is in cm.
How much work would be done on the ball between separation r = 4 cm and r = 2 cm?
Assume that the only force acting on the ball is friction:
If the ball has mass 50 grams, how fast would it be moving at x = 1 cm, if it was released from rest at x= 3 cm?
If the ball has mass 50 grams, how fast would it be moving at x = 1 cm, if it was released from rest at x= 4 cm?
If the ball has mass 50 grams, how fast would it be moving at x = 1 cm, if it was released from rest at x= 5 cm?
How much KE would be required at the x = 2 cm position to allow the ball to 'coast' out to the x = 5 cm position?
University Physics: The formula used here is F = .4 N cm^2 / r^2. Note that this is not an accurate formula for a magnetic dipole.
Give precise answers to the questions posed above.
Would it be possible to give the ball enough KE that it would 'escape' the magnet, never coming back? What is the minimum KE that would be required?

When the ball got stuck on the magnet, what was the shape of its path as it approached the magnet?
The ball curved more and more toward the magnet. More force as it got closer, so more acceleration as it got closer.
If we had a magnetic monopole, which would always attract the ball toward the center of the monopole and with greater attraction as the monopole was approached, then would it be possible for a ball with just the right speed to be 'slung' around the monopole, without being pulled all the way to the monopole, in such a way as to not roll off the edge of the table?
The Earth attracts the Space Station and other orbiting object, including the Moon, in much the same way a magnetic monopole, if such a thing existed, would attract the steel ball. However the gravitational field of the Earth is not magnetic in nature, but gravitational. The gravitational influence is spread over concentric spheres. The radius of the Earth is about 6400 km. The gravitational field has a strength of 9.8 m/s^2 at the surface. If we multiply the strength of the field by the area of the sphere over which it is spread, what do we get?
The surface area of the Earth is 4 pi * radius^2 = 4 pi * (6400 km)^2 = ... = 5 * 10^14 m^2.
Multiplying by 9.8 m/s^2 we get 5 * 10^15 m^3 / s^2.
The quantity you just calculated, the product of the strength of the Earth's gravitational field at the surface times the area of the surface, is called the gravitational flux of the field.
The gravitational flux is the same for any sphere concentric with and enclosing the Earth.
For an object orbiting 600 km above the surface of the Earth, this same gravitational flux is spread over a sphere whose radius is 6400 km + 600 km. What is the area of this sphere, and what must therefore be the strength of the gravitational flux of this field?
The area of the sphere on which the orbit occurs is 7000 km, which gives us total area about 6 * 10^14 m^2.
Dividing our total flux 5 * 10^15 m^3 / s^2 by this area we find that at the position of this orbit the acceleration of gravity is about 8.3 m/s^2.
How much gravitational force does an object of mass 30 kg experience at the surface of the Earth? How much force does it experience at an altitude of 600 km above the surface? How much work would gravity therefore do on the object if it was raised directly from the surface to the 600 km altitude?
At the surface of the Earth the force would be 30 kg * 9.8 m/s^2 = 294 N.
At the 600 km altitude the force would be 30 kg * 8.3 m/s^2 = 249 N.
If we multiply the average of these two forces by the 600 km displacement we will get a good estimate of the work. However the force is not a linear function of position, so this is only an approximation.
Experiment:
Roll a steel ball down a 2-foot ramp, onto a level ramp and off the edge of the table to some level between table and floor. Incline the ramp the same as everyone else's ramp, using 2 marble blocks to support one end of the ramp, with the other resting on a dime which is placed on the tabletop.
Determine the average horizontal velocity of the falling projectile.
Comparing your results with those obtained by others for whom the distance of fall was different, test the hypothesis that the horizontal velocity of the freely-falling ball is constant.
Write up your results and explain the following:
Why it took most of the class over 20 minutes to figure out the horizontal velocity once they got their data
Why it should not have taken this long. Be specific, with references to class notes, Introductory Problem Sets, stuff you should have memorized, assigned text reading and assigned text problems.
Experiment:
Place a steel ball on a shelf-standard ramp. Slope the ramp at least slightly. Place a magnet with one of its poles facing down the ramp.
Move the steel ball slowly toward the ramp. Not the proximity of the ball to the ramp at the point where the ball first accelerates toward the magnet.
For each slope:
Determine the gravitational force component down the ramp as a multiple of the mass of the ball.
Assuming ball diameter 2.5 cm and density 7.5 grams / cm^3, determine the force exerted by the magnet on the ball.
Plot the slope of the ramp vs. the proximity of the ball to the magnet.
Plot the force on the ball vs. its proximity to the magnet.
Plot the acceleration the ball would experience on a constant-velocity ramp vs. its proximity to the magnet.
Answer the following, assuming that the ball is on a constant-velocity ramp of infinite length, based on your best interpretation of your
If the ball was released from rest at a distance of 4 cm from the magnet, how fast would it be moving when it reaches the point 3 cm from the magnet?
If the ball was released from rest at a distance of 3 cm from the magnet, how fast would it be moving when it reaches the point 2 cm from the magnet?
If the ball was released from rest at a distance of 2 cm from the magnet, how fast would it be moving when it reaches the point 1 cm from the magnet?
If the ball wa released from rest at a distance of 4 cm from the magnet, based on your previous answers, how fast would it be moving when it reaches a point 1 cm from the magnet?
If the ball was 1 cm from the magnet, how much velocity would it have to be given away from the magnet in order to 'coast' to a distance of 4 cm before turning around and 'falling' back toward the magnet?
If the ball is 1 cm from the magnet, is it possible to give it enough initial velocity so that it moves away from the magnet, never coming back?
University Physics question:
Instructor Response consists of a note indicated by *&*& in the following:
Predicting the ramp slope that would be required for the steel ball to hit 3 cm closer to the direct-drop point?
This is what I have:
Rise is 7.5 cm
Run is 65 cm
vAve is 70 cm/s or .70 m/s
Vox is .70 m/s cos 187 deg. = -.69 m/s
Voy is .70 m/s sin 187 deg. = -.09 m/s
y-motion:
'ds = -.94 m
a = -9.8 m/s
Voy = -.09 m/s
If (Vo cos angle)time = (.70m/s)[cos(7 deg.)](.43 sec) = .30 meters or 30 cm
vAve = 'ds/'dt 27cm/4.3sec = 63 cm/s or .63 m/s
Rise = 5.3 cm
Run = 60 cm
angle = 5 deg.
'ds = 27 cm
So (Vo cos angle)time = (.63 m/s)[cos(5 deg.)](.43 sec) = .27 m/s or 27 cm
*&*& .43 seconds is the time required to fall if initial vertical velocity is zero. That isn't the case here. You have to solve the equations of motion for the given vertical information in order to get the correct `dt. *&*&
Is this correct?