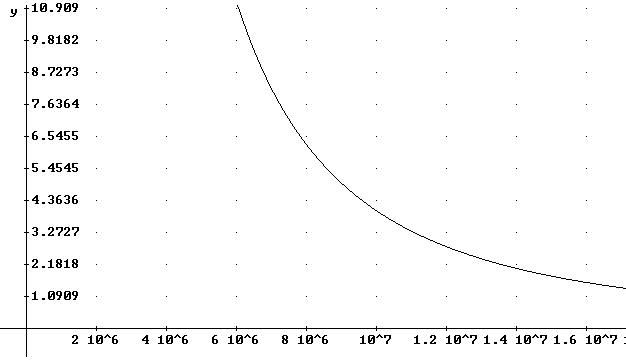
1110

• Run Multiple Choice Generator at h:\shares\physics
• General College Physics:  Run Core Problems by giving the program 174 as your 'course'--enter this when asked for your 3-digit course number.   Do the problems for 11/03.
• University Physics:  Run Multiple Choice Generator for 201 and choose 'Calculus of Uniformly Accelerated Motion'.
• If you miss a problem be sure to click on Comment and explain what you do and do not understand about the question and the given solution.

Using the gravitational field simulation  at

• bb.vccs.edu, login as vhstudent password college,
• select Supervised Study Current Semester Summer 04, then
• Course Documents > Downloads > Physics I > Gravitational Field Simulation

and do the following Simulation Experiments:

Gravitational Potential Function

By 'shooting' a satellite from the surface of the Earth to an altitude of 1.2 Earth radii, determine the PE change per unit of mass between these two points (based on a satellite mass of 1 kg, figure out the PE change in Joules, then divide by the 1 kg mass to get the PE change per unit of mass).  

Repeat, this time shooting from the surface to 1.4 Earth radii. 

Repeat once more, this time shooting from surface to 1.6 Earth radii. 

PE per unit of mass is called gravitational potential. 

We can measure gravitational potential relative to any chosen point.  What you have observed is gravitational potential relative to the surface of the Earth.

Make a table of your observed gravitational potential vs. distance r from the center of the Earth, with r in meters.  

Quickly make a copy of your data table and submit it as instructed.

Using your data plot three points on a graph of gravitational potential vs. r. 

For each of the three intervals of your graph, what is the average slope?

From the shape of your graph project, as best you can, the PE change from the surface to 2 Earth radii, and from the surface to 3 Earth radii.

Determine the initial velocity a projectile would require to just get from the surface to each of these distances (remember that PE gain is equal to KE loss).

Rescale your graph so that the horizontal asymptote is the horizontal axis and interpret.

For each of the three intervals of your graph, what is the average slope?

Compare with the function potential(r) = -G M / r.

Angular Velocities

Set a satellite in a circular orbit at a distance of 2 Earth radii and determine the angular speed of the simulated orbit in radians per second.  Do this in two ways. 

• First send out two straight 'shots' at angles which are 1 radian apart, just to obtain two lines which lie at a 1-radian angle.   Time the orbit between these two angles. 

• Second, simply time the simulation for 1 complete orbit.  Then repeat for an orbit at 3 Earth radii.

Discussion of Gravitational Potential Function

The force vs. position function for a 1 kg object is of the form F = k / r^2, where r is the distance from the center of the Earth.  As explained in the intro problem sets, k is a proportionality constant.  Since F = 9.8 N at the surface of the Earth we have F = 9.8 N when r = 6.4 * 10^6 meters.  Solving F = k / r^2 for k we obtain k = F * r^2 = 9.8 N * (6.4 * 10^6 m)^2 = 6.3 * 10^7 N m^2.  Our force vs. position function is therefore

• F(r) := (6.3 * 10^7 N / m^2 ) / r^2

If we graph F(r) vs. r we obtain the following graph:

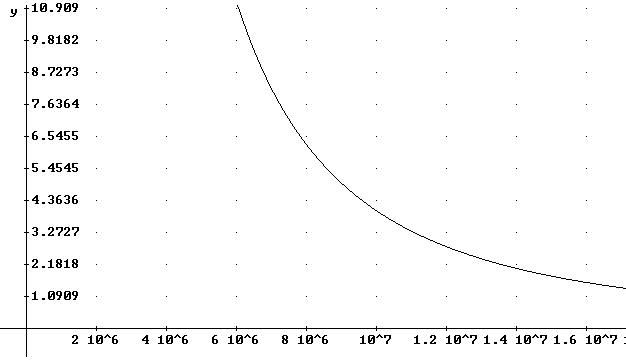
The work done on the object to raise it from one position to another is the area under the curve between thesse two positions.  For example the work to raise from 6.4 * 10^6 m to 1.2 * 6.4 * 10^6 m is the area between the two vertical lines on the graph below:

The PE change of an object from the surface of the Earth to distance r

at distance r from the center of the Earth, relative to the surface of the earth (this means that the PE is taken to be zero at the surface

The following statements will be rearranged into daily quizzes:

Statement 1108_01: 

The gravitational influence of the Earth is spread out over concentric spheres whose radius is greater than or equal to that of the Earth.  The gravitational influence is of equal magnitude at every point of a given sphere, and is directed toward the center of mass of the Earth. 

The radius of the Earth is about 6400 km and its gravitational influence at the surface is such that an object in free fall near the surface accelerates at 9.8 m/s^2 toward the center.  The strength of the field is measured at any point by the acceleration that would be experienced by an object in free fall at that point. 

From these facts it follows that the total gravitational flux of the Earth, defined as the product at every point of the radial component of the field strength and the area of a sphere concentric with the Earth, is for any such sphere equal to the surface area of the Earth multiplied by 9.8 m/s^2. 

• The surface area of a sphere is 4 p r^2, so the total flux is 4 pi ( 6.4 * 10^6 m)^2 * 9.8 m/s^2, which is close to 5 * 10^15 (m/s^2) * m^2 or 5 * 10^15 m^3 / s^2. 

To find the gravitational field strength at any distance r from the center of the Earth, provided r is greater than the radius of the Earth, we find the area 4 pi r^2 of the corresponding sphere and divide this into 5 * 10^15 m^3 / s^2.

Statement 1108_02: 

The total gravitational flux of an object is equal to 4 pi G m, where m is the mass of the object and G is the universal gravitational constant 6.67 * 10^-11 N m^2 / kg^2.  Knowing the total gravitational flux of the Earth to be about 5 * 10^15 m^3 / s^2, we find the mass of the Earth by setting 4 pi G m equal to flux and solving for m: 

4 pi G m = flux so

m = flux / (4 pi G) =

5 * 10^15 m^3 / s^2 / (4 pi * 6.67 * 10^-11 N m^2 / kg^2) =

6 * 10^24 kg, approx.

Statement 1108_03: 

If the mass of the Earth doubled without changing its radius, we would have double the gravitational flux at the surface, which would result in double the gravitational field.  So the acceleration of gravity would be doubled, which doubles the gravitational force exerted by the Earth on any given object at the surface.

If the mass of the Earth remains the same (as it does to several significant figures) then if the object you are holding doubles in mass, you have to exert twice the force to support it.  

If the mass of the Earth doubled and the mass of the object you are holding also doubled, gravitational field of the Earth would double, so you would have to exert twice as much force as before on the original mass plus this amount again on the added mass, so you would have to exert four times the force to support it.

Statement 1108_04: 

Two masses, each concentrated at a point, exert on one another a gravitational force, with each mass experiencing a force in the direction of the other.  More specifically, point masses m1 and m2, separated by distance r, experience a mutual attractive force of G m1 m2 / r^2 along the line joining the masses. 

If one of the masses is doubled it is as if an equal mass is superimposed on the original, and we get double the force.  If the other mass is then doubled, there is another doubling of the force.  In terms of the equation F = G m1 m2 / r^2, doubling m1 gives us F = G * 2 m1 * m2 / r^2 = 2 G m1 m2 / r^2, and doubling both masses would give us F = G * 2 m1 * 2 m2 / r^2 = 4 G m1 m2 / r^2.

If r was doubled then since we are dividing by the square of r, we would get 1 / 2^2 = 1/4 as much force.  In terms of the equation, we would have F = G m1 m2 / (2r)^2 = G m1 m2 / (4 r^2) = 1/4 G m1 m2 / r^2.

Another way to look at the doubling of r is that the gravitational flux would be spread over a sphere of double the radius, which would imply four times the surface area and therefore 1/4 the force.

Statement 1108_05: 

The work required to increase the separation of masses m1 and m2 from r = r1 to r = r2 is equal to the average force exerted over that interval multiplied by the displacement r2 - r1. This corresponds to finding the average vertical coordinate of the F vs. r graph between r = r1 and r = r2, then multiplying by the width of the interval.  That is, the work is equal to the area beneath the F vs. r curve between r1 and r2, which is the same as the definite integral of the F vs. r function between r = r1 and r = r2.

A graph of force vs. separation r for two given masses m1 and m2 is asymptotic to both the F and r axes, and is concave upward with the force decreasing at a decreasing rate from its asymptote along the positive vertical axis toward its asymptote along the positive horizontal axis.   Between any two values r = r1 and r = r2 of r the graph therefore lies below the straight line connecting the r = r1 and r = r2 graph points so that a trapezoidal approximation to the area under the curve is always an overestimate. 

If r2 > r1 then the greatest force will occur at separation r1 and the least at separation r2.  The average force will therefore be somewhere between G m1 m2 / r2^2 and G m1 m2 / r1^2.  {}{}If r2 / r1 is close to 1, then a graph of F vs. r will be nearly linear over that interval, and the average force will be nearly equal to the average of the two forces. In this case the area under the actual curve will be reasonably close to the trapezoidal approximation. 

If r2 / r1 > > 1 then the graph will dip significantly below the linear approximation and the trapezoidal approximation will be poor, resulting in a very significant overestimate.{}{}University Physics students note:  The actual area beneath the F vs. r curve, which is the integral from r1 to r2 of F(r) with respect to r, is equal to the change in the antiderivative function - G m1 m2 / r, called the potential function.

Statement 1108_06: 

The gravitational force is conservative.   If the two masses are separated from position r1 to position r2 then allowed to return unimpeded to the original separation, the KE gained in the return will be equal to the work done to separate the masses.

Gravitational PE change between two fixed masses is due only to the change in the separation of the two objects.

If no nonconservative forces act on an object in a gravitational field, then PE and KE changes are equal and opposite.  A satellite coasting in empty space experiences the same KE change between two orbital distances regardless of the path it takes (e.g., coasting straight toward or away from the planet or moving in a repeating elliptical orbit).  When an orbiting satellite moves from its maximum distance to its minimum distance its change in KE is identical to the change it would experience if it was 'dropped' from rest at the maximum distance to the minimum distance.

Statement 1108_07: 

The centripetal acceleration of a satellite in circular orbit is v^2 / r, where v is its speed and r is the radius of the orbit.  The strength of the gravitational field at distance r from a planet of mass M is G m / r^2 (we can get this from the fact that the force on another mass m is F = G M m / r^2, so the acceleration is a = F / m = (G M m / r^2) / m = G M / r^2; note that the strength of the gravitational field at a point is the acceleration of gravity at that point).  Setting v^2 / r = G M / r^2 we can solve for v to obtain v = sqrt( G M / r).  

The circumference of a circular orbit at distance r is 2 pi r.  So the time required for a complete orbit is

period of orbit = orbital circumference / orbital speed =

2 pi r / (sqrt(G M / r) ) =

2 pi r / (sqrt( G M) / sqrt(r) ) =

2 pi r / sqrt( G M) * sqrt(r) =

2 pi / sqrt(G M) * r^(3/2).

Statement 1108_08: 

In the gravitational field simulation you observed for a 1 kg mass the KE change from the 'low' point of an elliptical orbit, and you also observed the KE change of a 'straight' shot from the low to the high point.   Within experimental error the KE changes were identical.  This illustrates that the change in gravitational PE between two points depends only on the distances of those points from the center of the planet. 

You also observed that, starting from the planet surface, there is less change in PE for every

If you were to graph the gravitational PE vs. distance from the planet, the graph would be increasing but at a decreasing rate.  

The gravitational potential function for a point mass M is {}{}potential(r) = - G M / r.

This function is an antiderivative of the gravitational field function G m / r^2. 

The gravitational potential function measures the change in PE per kg between two points.