Physics I Class Notes, 8/26/98

Finding Change of position from velocity vs. time information; graphical representation by trapezoids

Position vs. Clock Time for uniform acceleration

Position vs. Clock Time graph

Introduction, Goals and Questions

Here we reason out a variety of questions regarding the changes in position that can be inferred from velocity vs. clock time information.  We do this first within the context of known initial velocity, a known constant rate of velocity change, and a given time duration.  We then consider position changes over a number of relatively short time intervals, and construct a position vs. clock time table and graph.

Today we:

• reason out changes in position from velocity vs. clock time information
• use trapezoids to visualize position change from initial and final velocity and time duration
• translate a graph of velocity vs. clock time into a table or graph of position vs. clock time.

Our starting example gives us the initial velocity, time duration and constant rate at which the velocity of an object changes.  This example leads to the following questions:

• Given the constant rate at which velocity changes, initial velocity, and time duration, how do we reason out the corresponding change in the position of an object?
• How do we determine position changes over specified time intervals from a graph of velocity vs. clock time, and how can we then construct a graph of position vs. clock time?
• In terms of the meanings of altitudes, area and width, how does a velocity vs. clock time trapezoid represent change in position? 
• How can a series of velocity vs. clock time trapezoids help us to calculate and visualize position vs. clock time information?

You will be asked to use the shape of the position vs. clock time graph to explain how to visualize the results of your experiment from the preceding class.

Finding Change of position from velocity vs. time information; graphical representation by trapezoids

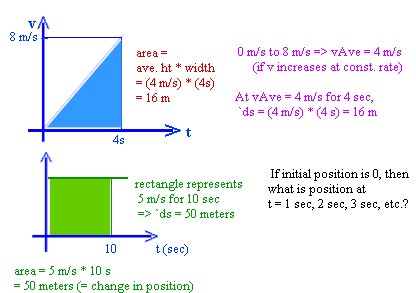
Suppose that the velocity of an object increases at a constant rate from 0 to 8 m/s in 4 seconds.  How are we to find the distance it travels in the 4 seconds?

• Rather than distance traveled, we will use the term position change.  Position change can tell us more than distance, since we can define position change in such a way that it is positive or negative, whereas distance is always positive.
• We know that if the velocity is constant (e.g., if velocity is 5 m/s as in the green graph below) the position change is equal to the product of velocity and time duration (e.g., at 5 m/s for 10 seconds the position change is 5 m/s * 10 s = 50 m). 
• The green graph shows how this calculation can be represented as the area of a rectangle with altitude 5 meters and width 10 seconds.

A graph of the changing-velocity situation shows velocity increasing along a straight line (i.e., at a constant rate) from 0 to 8 m/s in 4 seconds. 

• We can reason out the corresponding position change by noting that the average velocity seems to be 4 m/s (averaging 8 m/s and 0 m/s), so that in 4 seconds the position change is `ds = 4 m/s * 4 s = 16 meters. 
• Can we calculate this position change as an area, as we did with the constant-velocity situation of the green graph?

To calculate the area of the trapezoid under the graph (yes, it's a triangle, but a triangle is a trapezoid with one side equal to 0) we can multiply its average height times its width. 

• The average height of a trapezoid is just the average of its heights, which are 0 m/s and 8 m/s.  So the average height of the trapezoid below is 4 m/s. 
• Multiplying average height by width we multiply the 4 m/s average height, which represents average velocity, by the 4-second width, which represents time interval,  we get area (4 m/s) * (4 sec) = 16 meters, which represents the position change.

We see that the two ways of calculating position change correspond exactly.  The reason is fairly obvious:  the average height corresponds to the average velocity, since in either case we are averaging the initial and final velocities, while the average width corresponds to the time interval by which we multiply the average velocity.

Position vs. clock time for uniform acceleration

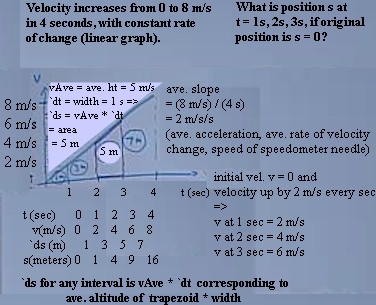
We now wish to determine the position at clock times t = 1, 2 and 3 seconds, assuming that the initial position is zero.  Since the position has changed by 16 m during the 4 seconds, we first conclude that at t = 4 seconds the position is s = 16 meters (we use s to denote position).

The bad-looking graph below shows the velocity vs. clock time line. 

• If we accept that change of position is represented by the area under the velocity vs. clock time graph, we can determine the velocities at 1, 2 and 3 seconds using similar triangles(e.g., if the trapezoid whose base goes from 0 to 4 seconds has final altitude 8 m/s, then the triangle with base from 0 to 1 second has final altitude 1/4( 8 m/s) = 2 m/s). 
• Alternatively we can use the concept of acceleration:  since velocity increases at a constant rate of 2 m/s/s (determined by the slope of the graph and corresponding to, for example, the speed of the speedometer needle), and since initial velocity is 0, the velocity goes up by 2 m/s every second and reaches 2 m/s after 1 sec, 4 m/s after 2 sec, 6 m/s after 3 sec.

Using the velocities we obtain, we can for any time interval determine the average velocity over that interval.  

• For example, between 2 and 3 seconds the velocity increases from 4 m/s to 6 m/s.   The average velocity is therefore 5 m/s, corresponding to the altitude of the indicated trapezoid. 
• Since this average velocity has a duration of 1 second, the position change during that second is (5 m/s) * (1 sec) = 5 meters.

The position changes during the time intervals are 1 m, 3 m, 5 m and 7 m, and are indicated by the circled numbers on the graph. 

• The total position change  up to a given clock time is easily found by adding the position changes during all the time intervals up to that clock time.

Note:  The following series of video clips is repeated on the notes for the next class.  They are related to the above calculations; they are directly related to the calculations in the subsequent set of notes.

Position vs. Clock Time graph

If we plot position s vs. clock time t we obtain the graph shown below. 

• We note that if the slope is calculated between two points of this graph, we obtain the average velocity between the corresponding clock times.  We might conjecture that the slope of a position vs. clock time graph represents average velocity.
• This graph of area under the velocity graph vs. clock time has slopes which give us back our average velocities.

We have started with a velocity vs. time graph, used its areas to obtain a position vs. time graph and used the slopes of this position vs. time graph to get back to the velocities we started with. 

• Present, past and future calculus students, and especially Physics 241 students, note:  This full circle is the essence of the Fundamental Theorem of Calculus.

Experiment

From your previous experiment, you know that the average velocity of an object rolling down a uniform incline is greater on the lower than on the upper half of the incline.

• How does the shape of the corresponding position vs. clock time graph, with its upward curvature, show us that the time required to travel the first half of the incline is greater than that required to travel the second half?

Distance Students

Do the following:

• E-mail a description of your answers to the experiment question.
• E-mail your answers to the questions posed at the beginning of these notes.

Further questions:

What would happen to our position vs. clock time graph if the position at t = 0 wasn't zero?

How are the velocity vs. time and acceleration vs. time graphs related?

How can we look at a graph of velocity vs. time and visualize a corresponding position vs. time or acceleration vs. time graph?

How can we look at a graph of position vs. time and visualize the velocity vs. time graph?

How can we look at a graph of acceleration vs. time and visualize a corresponding velocity vs. time graph?