Class Notes Physics I

Class Notes Physics I, 9/02/98

Lab Exercise; The Use of Flow Diagrams in Problem-Solving

Lab exercise

The use of 'flow diagrams' in analyzing problems

We conduct an experiment to determine acceleration vs. slope for a toy truck on small-slope inclines, which we extrapolate to obtain the acceleration of gravity. We then solve two basic uniform-acceleration problems (given v0=0, a and `dt, and given v0=0, `ds and `dt) by reasoning, then represent the solutions by 'flow diagrams' that reveal the structure of the problem.

Introduction, Goals and Questions

Today we

conduct an experiment to determine the relationship between the slope of an incline and the acceleration of an object down the incline
analyze two basic uniform-acceleration problems and represent the structure of their solutions using 'flow diagrams'
consider some useful strategies for problem-solving

For the lab exercise we begin with the idea that as the slope increases so does the acceleration of an object down the slope. We ask the following questions:

For small slopes does the corresponding acceleration seem to change by an amount that is proportional to the change in slope?
Do we expect the small-slope behavior of acceleration vs. slope to continue when the slope becomes large?
How are initial and final velocities, acceleration, time duration and displacement related in the situations we encounter in this experiment?

Lab exercise

This lab exercise is redundant with lab exercises assigned on the homepage, and need not be done at this time. However, you should view the clips.

http://youtu.be/obCt7QoQ0cs

http://youtu.be/ZMOgdrp2thg

http://youtu.be/oI2v5GaeWfg

Using a toy truck or car and a ramp raised at one end, on a slope such that the vehicle just barely accelerates down the incline, determine by timing the vehicle as it coasts down the ramp for a measured distance, starting from rest.

Use good timing technique and use at least three timings.

Measure the slope of the incline by measuring its rise and run.

Increase the incline slightly by adding a large washer under the raised end and repeat.

Add another washer to increase the incline and repeat again. Then add a final washer and repeat once more.

The things you have actually measured, the rises, runs and times, are your data. What we find from the data are not data and should not be reported as such.

Use your data to determine to the slope for each incline and the corresponding acceleration.

Sketch of graph of the acceleration versus the slope.

From your graph conjecture what acceleration would correspond to a slope of 1, assuming that the graph is linear (i.e., that it forms a straight line and that your graph is not perfectly straight because of uncertainties in timing and other measurements).

Estimate the uncertainty in your various measurements, and estimate the effect of these uncertainties on your results.

As we will see later, this acceleration corresponds to the acceleration of an object falling freely under the influence of gravity.

Conduct a modified experiment by finding slopes such that the acceleration of the cart is approximately .2 m/s/s, then .4 m/s/s, then .6 m/s/s (you might extrapolate your existing acceleration vs. slope data).

Again obtain a graph of acceleration vs. slope.
From your graph conjecture the acceleration that would correspond to slope 1, assuming that the graph is linear.

Is this modified strategy more or less accurate than the original strategy of using equal slope increments?

The use of 'flow diagrams' in analyzing problems

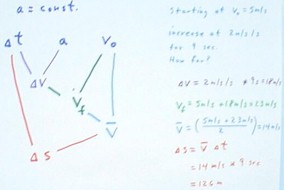
Consider the quiz problem from the present class, where an object starts out at initial velocity 5 m/s and for time duration nine seconds increases velocity at a rate of 2 m/s/s. We wish to determine how far the object travels during this time.

This problem is fairly easy to reason out.

If we increase velocity for nine seconds at the rate of 2 m/s/s, that are increase is obviously 18 m/s and we attain a final velocity of 5 m/s + 18 m/s = 23 m/s.
Our velocity therefore averages (5 + 23) m/s / 2 = 14 m/s, and in a nine second time interval we experience displacement (14 m/s) (9 sec) = 126 meters.

The process is depicted in the figure at left.

We represent the process symbolically on the 'flow diagram' figure below.

We began by calculating the velocity change `dv resulting from the acceleration a and time interval `dt. We represent this on the figure below by the 'purple triangle' (with purple lines leading to `dv, which is also in purple). This triangle indicates that the velocity change is obtained from the time interval and acceleration.
We next obtained the final velocity by adding the velocity change to the initial velocity. This is depicted by the 'green' triangle in which final velocity vf follows from velocity change `dv and initial velocity v0.
We then averaged the initial and final velocities to get the average velocity, which is depicted by the 'light blue' triangle.
We finally use the average velocity and the time interval to determine the displacement `ds, depicted as the 'red' triangle.

http://youtu.be/kB2Hxgl2iKg

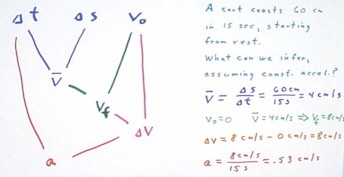
We can use the same strategy for the quiz problem from the preceding class, where a car coasts 60 cm in 15 seconds starting from rest.

Note that the information on this problem is different from the preceding, where we started with knowledge of `dt, a and v0. This time we start with knowledge of `ds, `dt and v0.

We can solve this problem by simply drawing whatever conclusion we can from the information we are given or have already concluded. This is preferable to sitting around paralyzed because we can't see the complete solution right away. This strategy is very often useful, because if we get 'hung up' on where we're trying to go we can fail to see where it is possible to go. The idea is to 'keep moving', even if it isn't clear where we're going. Of course, we want to stop every once in awhile and check our progress toward our goal.

The first thing we can conclude is that the car has an average velocity of 60 cm/s / 15 s = 4 cm/s.
We next conclude that, since the car started from rest and averaged 4 cm/s, it must have achieved a final velocity of 8 cm / s.
We are attempting to determine the acceleration of the car. Acceleration is velocity change divided by time interval. We know that there is a 15 second time interval, so we need only find the velocity change. We say that the velocity change from 0 to 8 cm/s is 8 cm/s.
We finally conclude that the acceleration is 8 cm/s / 15 s = .533... cm/s.

The 'flow diagram' below represents the process used above:

We represent the calculation of the average velocity vAve from the known time interval `dt and displacement `ds by the 'purple' triangle.
We represent our reasoning out of the final velocity vf from the initial velocity v0 and the velocity change vAve by the 'green' triangle.
We represent the calculation of velocity change `dv from initial velocity vf and final velocity v0 by the 'fuschia' triangle (it probably looks pretty much red).
We finally represent the calculation of acceleration a from the velocity change `dv and the known time interval `dt, using the 'red' triangle.

http://youtu.be/l30Dz609njc

You will do well to learn to construct such 'flow diagrams' as you solve multi-step problems, and you need to practice looking at such diagrams to see the structure of the problems you solve. The structural thinking encouraged by this process can be a very useful tool, demonstrating how a complex problem can be broken down into a series of simple, interlinked steps.

You might note that this last problem has a lot to tell you about how to determine the acceleration of those vehicles on the inclines, as in the lab exercise.