Cart, ramp and washer experiments
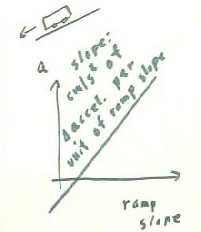
When a cart coasts down a constant incline we have seen that its acceleration is uniform and, at least for small slopes, the graph of acceleration vs. slope seems to be linear. The slope of the acceleration vs. ramp slope graph gives us the change in acceleration per unit of ramp slope; if the acceleration is measured in cm/second/second, or cm/second ^ 2, then the slope tells us how many cm / s^2 of acceleration we experience per unit of ramp slope. Values determined from carefully done experiments using toy cars and wooden ramps are generally within 10-15% of the ideal slope, which is 980 cm/second ^ 2, the acceleration of gravity.
The figure below depicts a cart rolling down in incline and a typical acceleration vs. ramp slope graph.
The figure below depicts a cart rolling down an incline and a typical acceleration vs. ramp slope graph.
When a cart-and-washer system is accelerated on a level incline by the force of gravity on a set of washers suspended over a low-friction pulley by a thread, the acceleration is seen to be linearly related to the number of washers. The slope of this graph is the acceleration increase per added washer. The figure below depicts this situation. (Note: the graph shown in this figure should intersect the vertical axis below the horizontal axis, not above it; the graph as shown seems to indicate a positive acceleration with no washers).
The net force acting on the system is the force of gravity on the washers, and is hence proportional to the number of washers suspended.
When data are corrected for frictional resistance, and when the mass of the system is kept constant by keeping any unused washers in the cart, the graph will ideally be perfectly linear and will pass through the origin. Such a graph indicates that the acceleration is directly proportional to the number of washers and hence to the net force acting on the system.
For any number of suspended washers, there exists a ramp slope such that the washers tend to pull the cart up the ramp without accelerating it. We might call this the constant-velocity slope for the given number of washers. When the constant-velocity slope is plotted vs. the number of washers, we again get a linear graph. The slope of this graph tells us how many units of ramp slope correspond to one washer.
From the first two graphs, where we get the acceleration change per unit of ramp slope and the acceleration change per washer, we should be able to determine how much change in ramp slope corresponds to addition of a washer. This last quantity is the slope of the third graph. If this prediction is close to the observed value, then we can say that the results of the three experiments are consistent.
If the three experiments are consistent then we can conclude that, for a given change in ramp slope, the change in the force accelerating the cart down the ramp is equivalent to effect of gravity on a number of washers which give the corresponding change in acceleration.
For example, if a change of .01 in ramp slope corresponds to change of 9.8 cm / sec^2 in the acceleration of the cart, and if the addition of a single washer corresponds to a change of 7 cm / sec^2 in the acceleration of the cart, then a change of .01 in ramp slope corresponds to the addition of somewhat more than one washer; the change in fact corresponds the addition of 9.8 / 7 = 1.4 washers. So a change of .01 in ramp slope corresponds to an increase in force which is equal to the force exerted by gravity on 1.4 washers.
The idea of work
When the washers descend, we think of gravity as doing work on them. When the cart ascends, we think of work being done on it to raise it. When the cart moves up an incline at constant velocity, the work done on it serves only to raise it; it doesn't speed up, so none of the work contributes to its speed.
Since more washers and more distance imply more work, we regard the work done on the washers as the force exerted on the washers by gravity multiplied by the distance through which they descend. Since a heavier cart moved through a greater vertical distance would be associated with more work, we think of the work done on the cart as the product of its weight and the distance.
The vertical distance moved by the cart is `dy = slope * run, which is approximately equal for small slopes to slope * displacement.
Two constant-velocity slopes are represented on the figure below, one greater and corresponding to a greater number of washers, and one less, with fewer washers. The carts are regarded as identical, so the greater number of washers will be associated with the greater slope. For the same displacement `ds of the washers, the equal displacements of the carts on the slope will result in a greater vertical rise `dy for the cart on the steeper slope. More work is therefore required to raise this cart. Since the greater number of washers will imply a greater gravitational force on the washers attached to this cart, gravity will do more work through the given displacement.
Another conclusion we can draw is twofold:
First, think of the situation in which a given number of washers, as corrected for friction (i.e., the number in excess of those required to overcome the friction in the cart) fall through a given distance.
The figure below depicts the cart on the constant-velocity slope corresponding to a certain number of washers. The washers necessary to overcome friction are indicated; the rest of the washers are regarded as contributing to the raising of the cart. The total gravitational force Fg is indicated by the red arrow, and the smaller frictional resistance f by the proportionally shorter purple arrow. We assume that the washers descend a distance `ds and the cart moves through displacement `ds on the incline.
The total force raising the cart is the difference F = Fg - f between the gravitational force on the washers and the frictional resistance. The work done by this force is the total force multiplied by the downward displacement of the washers.
The net force on the system consisting of the cart and washers, incidentally, is zero; otherwise the system would be accelerating, not moving at constant velocity. We will see later that the gravitational force component down the incline is in this case exactly equal to the force of gravity on the 'excess' washers not needed to overcome friction.
Our second conclusion it that when the cart is permitted to coast down a slope which exceeds the constant-velocity slope for a cart by itself, without washers, by an amount corresponding to the number of washers (corrected for friction), the effect will be identical to that of the same number of suspended washers pulling the cart down a constant-velocity slope.
Suppose for example that we find that the addition of a single washer in the second experiment results in the same increase in acceleration as an increase of .007 in the slope of the ramp. Then a single additional washer falling through a distance of, say, 40 cm will raise the cart an additional .007 * 40 cm = .28 cm in the vertical direction. If we have say 3 washers in excess of those required to overcome friction, then the constant-velocity slope will be 3 * .007 = .021, and when the washers fall through the 40 cm distance they will raise the cart .021 * 40 cm = .84 cm, three times as far as the cart would be raised by one washer. If the washers fall only 20 cm, they raise the cart only half as high. If they fall 80 cm they can raise the cart twice is high. If twice as many washers fall, the constant velocity slope will double, and for a given distance of fall they will raise the cart twice as high.
Furthermore, for the above situation, a slope of .021 in excess of the constant-velocity slope will result in the same acceleration as three washers (corrected for friction).
Experiment: Force vs. Acceleration for a car on a level track
The first and last experiments outlined above have been conducted. We now conduct the second.
Using different numbers of small lock washers attached to a thread hanging over a very low-friction pulley, we accelerated a toy car from rest through a known distance. The force exerted by gravity on the washers stretched the thread slightly, resulting in very nearly equal forces (unequal only because of the small amount of friction in the pulley) at both ends of the thread. The force at the end of the thread tied to the bumper of the car resulted in the acceleration observed. It should be noted that the force of gravity accelerated not just the mass of the car, but also the mass of the washers. For this reason the experiment should have been modified as follows: The washers to be used should have been placed in the car or truck and transferred to the hook at the end of the string one at time.
Our goal was to determine how the acceleration of the vehicle was related to the accelerating force. To find the acceleration corresponding to each number of washers, we used the time interval and the distance through which the car accelerated. In order to facilitate our calculation of the different accelerations, we used the basic formula in which our known quantities v0, `ds and `dt are found along with the desired quantity a. This equation is `ds = v0 `dt + .5 a `dt^2.
To avoid a lot of calculation we solve this equation for a, being careful to use valid laws of algebra at each step. We began by adding -v0 `dt to both sides, thus isolating the term .5 a `dt^2. We then multiplied both sides by the reciprocal 2 / `dt^2 of the coefficient of a. We finally used the distributive law of multiplication over addition (in the last step acceleration a is seen to be the product of 2 `ds + (-` v0 `dt) and 1/`dt^2, to which the distributive law of multiplication over addition applies), and we end up with a = 2 `ds / (`dt^2) - 2 v0 / `dt.
A sample of the data obtained is shown below. It took 5 washers to overcome the friction in the wheels of the truck, after which, as expected, each additional washer accelerated the truck through the 49 cm distance, from rest, in decreasing time intervals. The resulting accelerations, in cm/second^2, are easily calculated from the equation derived above. The equation is considerably simplified by noting that the initial velocity v0 was zero, and that `ds was always 49 cm. Using these quantities we see that for the present situation a = 98 cm / `dt^2. This makes all the work of deriving the formula for the acceleration worthwhile.
Using DERIVE (where we offered the function a(dt) := 98 / dt^2 after declaring the variable dt), we obtained a graph which seemed to be linear and the best-fit function a = 6.8 F - 6.5, where the force F is expressed as the number of washers.
We concluded that acceleration and force are very plausibly related by a linear function. We also see that this linear function very nearly passes through the origin, with the -6.5 being a systematic displacement of the graph points due to the friction in the car wheels. Thus this experiment supports the contention that acceleration and force are proportional.
The proportionality of acceleration and force is in fact one of the major tenets of physics, and was first formulated by Isaac Newton over 300 years ago. This proportionality is most often expressed as
F = ma
and is known as Newton's second law. This law tells us how to find the acceleration due to a given force on a given mass.
"