Work and Energy: Rubber Band accelerating Rail

Class Notes Physics I, 9/21/98

Work and Energy: Rubber Band accelerating Rail

Here we analyze an experiment in which we compare the F * `ds product in stretching a rubber band to the F * `ds product in sliding a rail accelerated by the rubber band across the floor. We also observe qualitatively some of the thermal properties of the rubber band. This provides an example of the work-energy theorem.

Questions:

We put energy into the rubber-band-and-rail system, in the form of the work we do stretching the rubber band. In detail, what happens to this energy from the instant we start pulling back to the instant the rail stops?
What happens to the KE of the rail as it slides across the floor? Where does it go?
From the point of view of the rail, is it doing positive work or negative work as it slides across the floor?
Does the rubber band supply more or less energy to the rail than the energy we put into it, and where does the difference go?
Does the rubber band exert more or less average force when it accelerates the rail than when it was pulled back?
Is a cooler rubber band stiffer or less stiff than a warmer one?

http://youtu.be/V7I-QpKIVGw

http://youtu.be/ZPfQgQkvXZE

The figure below depicts the curved-end ramp in the lab kit.

Though it is hard to see, a rubber band tied to a secured string is looped around the left end of the ramp, or the 'rail' as we will choose to call it for the purposes of this experiment (since its ramp function is irrelevant, we decided to choose a different name).
The string is secured to the leg of a heavy table, so that when the rail is pulled back (to the left) the string will remain relatively fixed rubber band will be stretched.

In the next figure the rubber band has been stretched as the rail was pulled back.

The original position of the end of the rail, and its new position, are clearly marked by arrows.

When the rubber band was suddenly released, the rail was thrust forward and ended up in the position indicated in the figure below, with the arrow marking the end of the ramp.

Question: If the rail is pulled back twice as far, stretching the rubber band twice as much, do we expect that the rail will go twice as far, more than twice as far, or less than twice as far?

Think about this question carefully before reading further.

The rail is now pulled back to a position twice as far from its resting position as before.

How far will it go when released?

The rail is seen to go considerably further than before.

Blue arrows indicate the first pullback and the distance traveled from the original position on the first release.
Red arrows indicate the second pullback and the distance traveled from the original position on the second release.

How many times further did the rail travel when the pullback was doubled?

Can you explain this observation? Was it expected?

http://youtu.be/DoexAZfQ-_g

We now turn to the question of how much force is associated with the stretching rubber band.

Obviously the force changes, increasing as we stretch the rubber band further and further.

We measured this force vs. stretch relationship using a lab scale and a meter stick.

One end of the rubber band is attached to a fixed support.
We actually measured distances associated with the stretching rubber band in cm; however on this series of pictures we use inches because they can be seen more clearly.

We see that when we stretch the rubber band so that the end attached to the balance moves from the 3.5-inch position to the 4.2-inch position, the spring in the balance stretches and therefore the reading on the balance increases.

Stretching the rubber band until it then reaches the 5.3-inch position, we see that the spring in the balance stretches even further and that the reading increases further.

If we record our spring reading and end position data, we can use it to determine how much stretch was associated with each force.

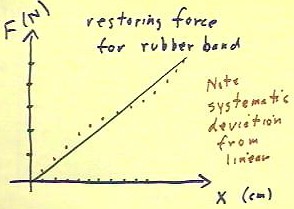
The graph we obtain might well look like that in the figure below.
A straight line is depicted which attempts to come as close as possible to the points, on the average.
We notice systematic deviation from linear behavior, with the graph points first moving further and further above the straight line, then back to it, then further and further below the line, and finally back toward the line.
This indicates that the rubber band does not give us a precisely linear force vs. stretch relationship.

http://youtu.be/SOz9JPyxY6c

http://youtu.be/EXcJ1HUI1TA

http://youtu.be/gDgBFPBy-ZI

http://youtu.be/Xyok5JZ3YSs

We now forget about the data points and concentrate on the straight line that best fits them, keeping in mind however that the straight line is not a perfect model for a rubber band.

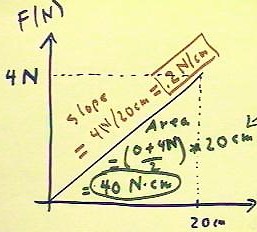
In the example below we find that a 20 cm stretch seems to increase the force by 4 Newtons.
We therefore calculate the slope of the graph to be .2 Newtons/cm.
This means that every cm of stretch appears to add approximately .2 Newtons to the force.

We also calculate the area under the graph between 0 and 20 cm, multiplying the average height of the graph by its width.

The average height is found by averaging the heights 0 and 4 N; the width is 20 cm. So the area is 40 N cm.

Recalling that work is defined as the product of average force and displacement, we see that our area calculation is identical to the calculation of the work.

We also note that the slope of the graph, the number of Newtons of additional force associated with an additional stretch of 1 cm, is a property of the rubber band.
We call this property the force constant of the rubber band.

(University Physics students:) As you know the area under a curve can be found by doing an integral.

In this case, if x represents the stretch of the rubber band, the force function of the above graph is clearly F(x) = .2 N / cm * x.
If we integrate this function between x = 0 and x = 20 cm, we obtain 40 N cm, as you easily can, and should, verify.

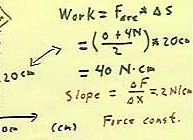
http://youtu.be/-nWznjWLttE

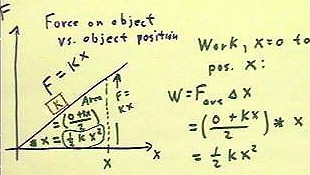
We can generalize these calculations by noting that if a force F = kx is exerted to move an object, as was done when we pulled the rail back against the force of the rubber band, the product of average force and distance is 1/2 k x^2.

(Note: the graph below is improperly labeled. Rather than 'Force on object ...', it should read 'Force to move object'. The force on the object might be interpreted as be F = - kx, directed opposite to the displacement x).
Between positions 0 and x, the force increases from 0 to kx.
The area under the resulting graph is then area = ave. ht * width = (0 + kx) / 2 * x = .5 k x^2.
This area again corresponds precisely to the work done in moving the object, obtained by multiplying the average force by the displacement.

http://youtu.be/SYTjuXPjf4A

What does all this have to do with how far the rail will slide across the floor?

We can arrive at a plausible answer to this question by looking at the force the rail needs to exert in order to move and the distance it moves.
If the rail experienced no friction, it would move along the level surface at a constant velocity forever.
However there is a frictional force between the floor and the rail, resisting the motion.
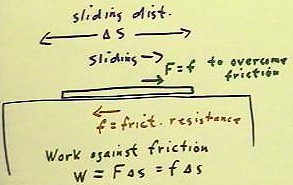
If we let f stand for the magnitude of the frictional resistance, indicated in the figure below by a red arrow directed opposite to the motion of the rail, we see that the rail must exert a force F of magnitude equal to f in the opposite direction to overcome friction.
The rail therefore does work against friction, with work = force * distance = | f | * |`ds|.

http://youtu.be/Cw1GyLd5hvc

It should at least be plausible that the amount of work required to pull the rail back will be equal to the amount of work done by the rubber band on the rail when the rail is released (since we expect the rubber band to exert the same force at the same position in whichever direction the rail happens to be moving), and that this might be equal to the work the rail has to do against friction before it stops.

We can therefore interpret the situation somewhat as follows:

When we pull the rail back, we do work which will be recovered after we release the rail.
This work will therefore be present in the rail in the form of energy of motion.
Before we release the rail, this work is potentially there; the potential will become reality after we release the rail.
At the instant the rail reaches its original position the rubber band ceases to accelerate it, and it has its maximum energy of motion.
As the rail slides across the floor, this energy is dissipated in the form of work done against friction.
This continues until all the energy is dissipated and the rail stops.

The energy that was potentially present in the rubber band, which was equal to the work we did when we pulled the rubber band back, is called potential energy, abbreviated PE.

From our graph of F vs. x, and our knowledge that the area under the graph from 0 to x is the approximate work .5 k x^2 done in stretching rubber band, we see that the potential energy of the rubber band is .5 k x^2.
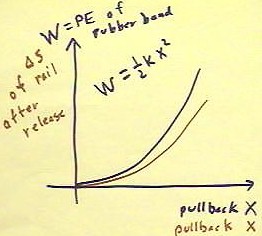
This function is graphed in blue in the figure below.

In the same figure we make the red graph of the displacement of the rail after its release from the rubber band vs. the pullback.

The data for this graph were obtained by observation.
The graph is seen to have essentially the same shape as the potential energy graph: theoretically if we choose our vertical scale just right the graphs would coincide.

This is exactly what we would expect if the frictional force f is constant.

If that is the case then, if f `ds = .5 k x^2 (that is, if the work done against friction as the rail slides is equal to the work done on it by the rubber band as it accelerates the rail), then we have `ds = .5 k x^2 / f = (.5 k / f) * x^2.
This graph is just a vertical stretch by factor 1/f of the graph of .5 k x^2. This relationship expresses the proportionality of `ds with .5 k x^2.

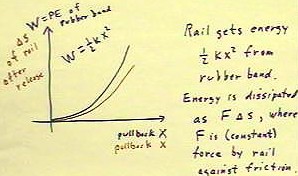
The figure below shows the graph and states the interpretation that the rail obtains energy equal to.5 k x ^ 2 from the rubber band, and that this energy is then dissipated as f `ds.

This is an application of the work-energy theorem, which states that the energy of a closed system is conserved.
We will see a more complete statement of this theorem soon.

http://youtu.be/7mDjiIPQbbA