Force, Work, Energy

Class Notes Physics I, 9/25/98

Forces, work energy

Experiment and Newton's Second Law: Analysis by Linear Equations

Work and Energy with the Friction Car

From the linear relationships between net force and slope and acceleration vs. slope for a cart on small-slope incline, we eliminate slope and obtain the relationship between net force and acceleration, obtain a direct proportionality. The proportionality constant is the mass m of the cart. The proportionality is expressed F = m a. This is Newton's Second Law.

By analyzing the trapezoid representing velocity vs. time, we obtain the two basic equations of uniformly accelerated motion. We eliminate `dt to obtain a third and vf to obtain a fourth equation. From the resulting four equations we can easily solve any uniformly accelerated motion problem, given three of the basic quantities vf, v0, a, `ds and `dt.

Combining Newton's Second Law with the third equation of motion we obtain the statement that the work done on an object by the net force on the object is equal to the change in the kinetic energy of the object.

For an object sliding down an incline, its weight components W sin(`theta) and W cos(`theta) parallel and perpendicular to the incline, combined with the condition of equilibrium perpendicular to the incline, tell us that the normal force exerted by the incline on the object is equal in magnitude to the perpendicular weight component, while the parallel weight component is opposed only by the frictional force. The frictional force is determined by the coefficient of friction and the normal force.

When an object coasts a distance up a frictionless incline, the work it does against the parallel component of its weight is equal to the work the would be done against gravity if it was lifted straight up for a vertical distance equal to the change in its altitude.

Questions:

How does the velocity vs. clock time trapezoid give us the two basic equations of motion?

When a wound-up friction car is released on the level surface, what do we see as a result of the potential energy conversion?

When a wound-of friction car is released up a ramp, what to we see as a result of the potential energy conversion?

What forces act on an object sliding up or down an incline?

What energy changes take place as an object slides up or down an incline?

If we know the mass and length of a pendulum, how can we determine the force required to displaced pendulum a given small distance from equilibrium?

Experiment and Newton's Second Law: Analysis by Linear Equations

To again summarize the results of experiments relating force, acceleration and slope, we see that the graph of net force F vs. slope m appears to be linear, as do the graphs of acceleration a vs. slope m.

We can eliminate slope from the linear functions that best model these two graphs to obtain a linear graph of force F vs. acceleration a.
This linear graph passes very near the origin and, within the limits of experimental error, seems to be a direct proportionality.
For the proportionality constant we use m, so that the equation is F = ma.
We identify m with the mass of the object being accelerated, and declare that when the mass is measured in kg and the acceleration in m / s^2, the force F will be in Newtons, where one Newton is the net force required to accelerate 1 kg at 1 m/s^2.

We also observed that the acceleration of a system of constant mass, due to the gravitational force on a number of small masses suspended over a low-friction pulley, is proportional to the number of these masses.

Equations of Motion, Newton's Second Law and Work

We also note that when acceleration is uniform, giving us a linear velocity vs. clock time graph, the displacement between any two clock times is equal to the area of the trapezoid corresponding to the area under the v vs. t graph between the two given clock times.

This area is equal to the product of the average altitude of the trapezoid and its width, which gives us the first basic equation of uniformly accelerated motion `ds = (v0 + vf) / 2 * `dt.
Under the same conditions the slope of the graph will be the acceleration a, and the change in velocity between two clock times will be represented by the rise of a slope triangle who slope is a and whose run is the time interval `dt between the two clock times.
The velocity change will therefore be `dv = a * `dt, and the final velocity will be equal to the initial velocity plus this change: vf = v0 + a `dt.
This is the second basic equation of motion.
From the two equations obtained from these pictures we can easily eliminate either `dt or vf, obtaining two more equations of uniformly accelerated motion which we regard as basic.
The equation we obtain when we eliminate `dt is vf^2 = v0^2 + 2 a `ds.

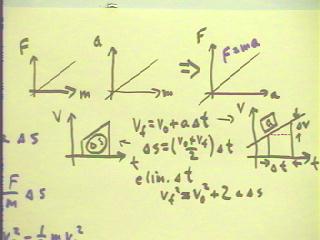
We can combine the two relationships F = ma and vf^2 = v0^2 + 2 a `ds, solving the first for acceleration a and substituting it into the second to obtain the third equation in the figure below.

If we solve this equation for the product F `ds of net force and displacement, we obtain the fourth equation.
If we identify F `ds as the work done by the net force on the object as we move through displacement `ds, and identify .5 m v^2 as the energy of motion or kinetic energy of the object, we see that the work done by the net force is equal to the change in the kinetic energy of the object.

You should understand how the experiments done so far motivate and illustrate the profound ideas implicit in this picture.

Work and Energy with the Friction Car

http://youtu.be/Psy05sa6_Hk

By measuring the force and distance required to 'wind up' the back wheels of a friction car by pulling the car backwards, we can determine the work required.

If we then allow the car to climb an incline, we can determine how much work was done against gravity and we can compare this work with the work required to wind the wheels.

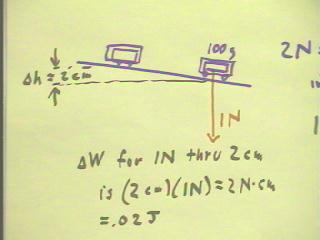
In class we found that a force of approximately 2 Newtons was required as we pulled the car back 10 cm.

The work done was therefore 20 Newton cm, or .2 Joules.
When the car was then allowed to run up an incline, its altitude increased by 2 cm.
The mass and weight of the car were found to be approximately 100 grams, or .1 kg, and one Newton.
To raise a 1 Newton weight 2 cm requires work 2 Newton cm or .02 Joules.
This account for only about 10 percent of the energy required to wind the wheels.
It is not clear where the other 90 percent went; thouch certainly some thermal energy was lost in the process, we would not expect that 90% of the input work would end up as thermal energy.
However, the energy had to go somewhere, and dissipated thermal energy looks like the best candidate.

http://youtu.be/hKcnmIPxLVg

We can also compare the .2 J of work done with the KE attained by the car when released on a level surface.

If all the work done goes into the elastic potential energy of the car's mechanism, and if all this energy is then converted to kinetic, we can use the definition .5 m v^2 = KE to predict the velocity.
We solve the equation for v to obtain v = `sqrt(2 * KE / m), and substitute .2 J of presumed KE and .1 kg of car mass to obtain the velocity prediction v = 2 m/s.

When we observe the car in this situation, we see that it attains a maximum velocity of only about .5 m/s.

Its kinetic energy at .5 m/s would be only 1/16 the kinetic energy at 2 m/s (since KE is proportional to the square of velocity, and object with .5 / 2 = 1/4 of its predicted velocity will have only (1/4)^2 = 1/16 of the predicted KE).
Since the maximum velocity was approximated visually, this result is pretty consistent with the observation that the car climbs only about 1/10 as high as expected.

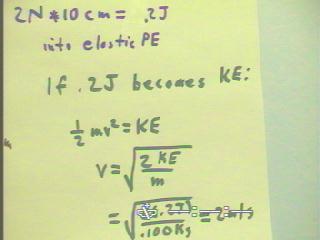
Object on Incline

http://youtu.be/4ezk_WhNdQE

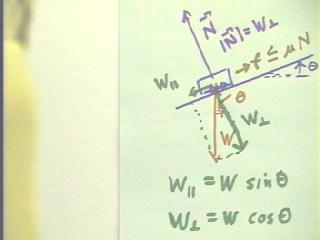
The figure below depicts an object on an incline, and the forces acting on it.

We replace the weight force W with two components Wparallel and Wperpendicular, which can be thought of as forming the sides of a rectangle whose sides are parallel and perpendicular to the incline and one of whose diagonals is the vector representing the weight.

In the absence of any external forces, the perpendicular component of the weight will tend to slightly bend the incline, which will exert an elastic restoring force perpendicular to its surface, which perfectly balances this weight component.
This force is called the normal force, indicated by the letter N with an arrow over the top to indicate that it is a vector quantity and to distinguish it from the unit N, the abbreviation for Newtons.
In this situation, with no external forces, the normal force N will be equal and opposite to the perpendicular component of the weight.

The parallel component of the weight will tend to accelerate the object down the incline.
A frictional force will tend to oppose this motion.
Up to a certain angle of incline, the frictional force will exactly balance the parallel component of the weight.
Beyond this angle friction will be unable to match the parallel component of the weight and the object will begin accelerating down the incline under the net influence of the parallel component and the lesser frictional resistance.

The frictional resistance os proportional to the force pushing the mass and the incline together.
This force is the normal force.
The frictional force can be anything up to and including some multiple of the normal force.
For example the frictional force for certain incline and a certain object could be anything up to a limit of 15% of the normal force; using f for the magnitude of the frictional force and N for the magnitude of the normal force we would then say that f <= .15 N (the <= stands for ' less than or equal to').
In general we use the Greek letter `mu to stand for the limiting proportion of the normal force which is available as friction.
We thus write f <= `mu N (no how the Greek letter `mu is written in the figure below).
`mu is called the coefficient of friction for the object and the incline.

Simple geometry and trigonometry show that when the incline angle is `theta the parallel and perpendicular components of the weight vector are respectively W sin`theta and W cos `theta.

http://youtu.be/91y2HT5SPrY

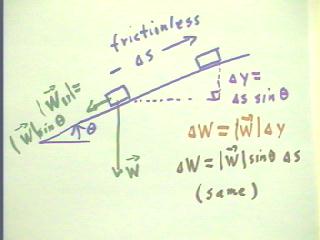
To see more clearly the energy situation related to sliding an object up a ramp, we consider an object of weight w (we will use lowercase w here to represent weight and uppercase W to represent work; in the figure below weight is represented with a small arrow over the top of the W rather than by a lowercase w).

The object is on a hypothetical frictionless incline at angle `theta from horizontal.
The parallel component of the weight is therefore wParallel = w sin(`theta), and if we slide the object a distance `ds along the incline at a constant velocity we will have to exert the force equal and opposite to this component.
As a result we do work `dW = w sin(`theta) * `ds.

On the other hand if we simply raise the object vertically through a distance equal to its vertical rise, we will have to exert a force equal in magnitude to its weight.

The vertical distance through which we lift the object will be `dy = `ds sin(`theta), so the work done will be `dW = w * `dy = w * (`ds sin(`theta)).
It should be clear that this is the same work contribution found before.

We therefore conclude that, as long as dissipative forces are not present, the work done in sliding an object up an incline is equal to the work done in raising the object vertically through the corresponding vertical distance.

Force on a Pendulum

http://youtu.be/gXxMeqCcwbc

When a pendulum of length L is displaced a distance x from its equilibrium position by a force F, which is pictured below as being slightly above the horizontal and which should be regarded as horizontal for small displacements x, the forces on the pendulum will be in equilibrium (i.e., they will add up to 0 so that the pendulum can remain stationary) if the tension force directed along the pendulum string has a vertical component equal to the weight and horizontal component equal to F.

For small displacements, we will have equilibrium if the ratio of F to the weight is the same as the ratio of the displacement x to the length L. That is,

F / mg = x / L.

This approximation is accurate to within better than 99.5% whenever x is small enough that x / L < .1 (i.e., x is less than 10% of the length of the pendulum).

http://youtu.be/pM8yI88sT_g