Class Notes Physics I, 9/28/98
Energy and Projectile Motion
We observe the horizontal distance `dx traveled
by a projectile projected from horizontally from an incline as a function of the
vertical altitude change `dy on the incline. We see that `dy appears to be
proportional to `dx^2.
We can understand this apparent proportionality
from energy considerations. The KE attained on the ramp is proportional to `dy
and to v^2, so the velocity v attained on the ramp is proportional to `sqrt(y).
Since the horizontal velocity of the projectile is constant, the horizontal
distance `dx it travels is proportional to v and hence to `sqrt(y). Since `dx is
proportional to `sqrt(y), y is proportional to `dx^2.
Not all the potential
energy lost as the ball rolls without slipping down the ramp ends up as the
kinetic energy 1/2 m v^2. Some of course goes into work against friction, but
most of the difference is accounted for by the fact that even in the absence of
friction 2/7 of the potential energy change would go into the rotational kinetic
energy of the ball. This explains why the ball doesn't travel as far as our
preceding energy analysis would indicate.
Questions:
- Why do we expect the velocity attained by a
ball on a ramp to be proportional to the square root of the vertical
position change of the ball?
- Why do we expected distance traveled by a
ball after being projected horizontally off of a ramp and falling a fixed
distance to be proportional to the velocity with which the ball leaves the
ramp?
- Why is the distance traveled by the
projectile in this situation less than that predicted from the velocity v,
where v is determined by setting 1/2 m v^2 equal to the potential energy
loss on the ramp? Why is the distance still less even if frictional losses
are taken into consideration?
Experiment: Energy and Horizontal Range of a Projectile
http://youtu.be/6Ki4AKRbc3M
http://youtu.be/X1tKkD8hGGU
When a ball
rolls down a ramp from
rest its potential
energy decreases, with a resulting increase in
its kinetic energy.
- If the ball is then projected in
the horizontal direction with
the resulting velocity and
allowed to fall freely through
some distance `dh,
the horizontal distance it
moves will clearly be greater when
the velocity with
which it was projected isgreater.
- We will investigate the energy
relationships and the kinematics of
this situation.
We set up the curved-end
ramp in such a way that its curved
end lies level at
the edge of
a horizontal tabletop.
- We will allow a ball to roll
from rest down the
incline from various
positions, recording data that
allows to determine the
distance `ds moved down
the ramp, the change
`dy in the altitude of
the ball from the instant
of release to the instant itleaves
the ramp, and the horizontal
range `dx of the ball
from a point on the floor directly below the
point at which it leaves the ramp.
- Note that when the ball rolls from
the edge of the ramp,
since the ramp is at that point horizontal the
ball's velocity will
be solely in the horizontal
direction, with zero
vertical component.
We will determine and
try to explain the
relationship between the horizontal
range `dx and the vertical
change in position `dy on
the ramp.
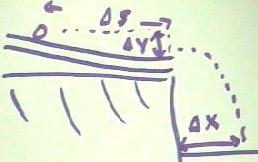
When we conducted the experiment we obtained the results represented
in the table below.
- We note that the ramp appears to have had a constant
slope between the 20
cm and 60
cm positions, with a rise of
a bit less than .9 cm per 10
centimeters of ramp.
- The 3.3
cm observation for `dy should
probably have been 3.4 or
3.5 cm.
The first thing we note is that the horizontal
ranges `dx change less and less, while
the change in altitude on
the ramp, `dy,
changes by roughly the same
amount each time.
- So any idea we had that `dx might
be proportional to `dy seems
to be shot.
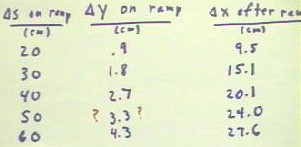
A graph of
the `dx vs. `dy (note
that we control `dy and not `dx, so that `dx is the dependent variable) shows
this decreasing change in `dx per
unit of change in `dy.
- University Physics students
note that the derivative dx
/ dy is therefore positive (dx
keeps increasing,
as expected) and decreasing (the second
derivative of range x
with respect to y = vertical distance on the ramp is negative;
the graph is concave
downward).
http://youtu.be/ZAj-RL-aG40
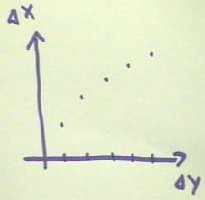
In an attempt to establish some
sort of proportionality between `dx and `dy,
the graph suggests that we might try looking at `dx^2
vs. `dy.
- When we do we find that,
except for the first
point, the relationship appears to be pretty much linear.
- If the anomaly of the first
data point is the result
of a systematic error,
for example in locating the range corresponding
to `dy = 0,
which we used for a starting
point in measuring `dx,
it is conceivable that `dx^2 might
be directly proportional to`dy.
- If so we would have `dx^2
= (constant) * `dy.
http://youtu.be/3vKRq2oXwcs
We will assume that `dx^2 is
indeed proportional to `dy,
and will try to explain this
by considering the energy
situation corresponding to a change
`dy in the altitude of
a mass m.
To raise the mass a distance
`dy, at a constant
velocity (so that KE remains
unchanged), we must exert a force
equal and opposite to
that exerted by gravity on
the object.
- This gravitational
force has magnitude
mg, and is the weight of
the object (designated by w
= mg in the figure
below, with the arrows over
the w and the g indicating that weight and gravitational acceleration are vector
quantities, with specific
directions).
- Since we are raising the
mass through vertical
distance `dy, the work is
the product of the weight and
the vertical displacement, `dW
= m g `dy.
- (Note the use of capital W for work and
lowercase w for weight; the absolute value signs around the g vector
just means that we refer to the magnitude of the gravitational
acceleration and not its direction, so |g| is approximately 9.8
meters/second ^ 2).
The work
`dW corresponds to the increase in
the gravitational potential
energy of the object.
- When the object is released from rest and rolls
or falls back down through
an equal downward
displacement `dy, this potential
energy will ideally convert to kinetic
energy.
- In this case, setting the potential
energy decrease equal to
the kinetic energy
increase gives us .5
m v^2 = m g `dy; we
easily solve to obtain v
= `sqrt(2 g `dy).
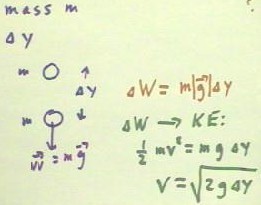
We note that in this relationship v is proportional to `sqrt(`dy).
- It follows immediately that v^2 is proportional to `dy,
so we could write v^2 = (konst)
* `dy.
- We noted earlier that `dx^2 seems
to be proportional to `dy,
so that `dx should
be proportional to `sqrt(`dy).
- If we put these proportionalities together
we can conclude that `dx is proportional to
the velocity v with
which the ball is projected horizontally from the ramp.
If `dx is proportional
to v, and if the time
required for the ball to reach
the floor after leaving the
ramp is the same regardless of
the horizontal velocity,
then the likely conclusion is
that the horizontal velocity of
the ball remains constant.
- In that case we would have
a consistent `dt,
and `dx = v `dt would express our proportionality.
- That `dt is consistently
the same is easily demonstrated by
flicking a washer
horizontally off the edge of
a table and
at the same time dropping another washer from
the same height --
they strike the floor
together, indicating the same
time `dt of fall.
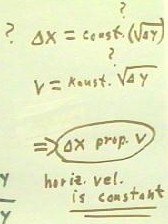
As a numerical
example we can calculate the potential
energy change and the corresponding
velocity attained by a ball
as it drops .9 cm.
- The potential
energy loss is m
g `dh = m (980 cm/s^2) (.9 cm), and
is set equal to
the kinetic energy .5 m
v^2 attained by the
object dropped from rest.
- The solution to
the equation is easily
found to be v
= 42 cm / s.
- We could repeat this
calculation for any `dy;
we will of course always obtain velocity
v = `sqrt(2 `dy / g), as
found earlier.
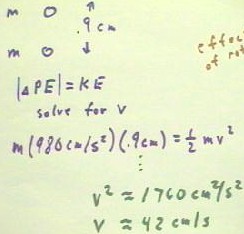
If we actually measure the velocities
attained by the ball, we
find that they are somewhat
less than those predicted by
our assumption that all the potential
energy goes into the kinetic
energy associated with the velocity
v of the ball .
- This is due mostly to the fact that in
addition to attaining
a velocity v the ball
also rolls, and
is a result gains a kinetic
energy associated with
its rotational motions.
- It turns out that, even in an ideal
situation were there is no
frictional loss, a ball rolling down
a smooth ramp without
slipping will have 2/7 of
its potential energy loss converted
to rotational kinetic
energy (the 2/7 might or
might not be accurate; we will see for sure when we analyze rotational
motion and rotational KE).
- This means that the kinetic
energy associated with
the velocity v,
which is called the translational
kinetic energy, should theoretically be only 5/7 of
the potential energy loss.
- In this situation, where the ball is
rolling down a grooved
ramp, it actually attains a slightly
higher rotational kinetic energy and translational
kinetic energy will be even
less than the 5/7
|`dPE |; friction will reduce observed translational
kinetic energy even a
bit more.
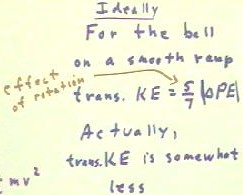
http://youtu.be/32fbL-EUaxM
We can easily
calculate the time
required for the ball to fall the 94
cm from the edge
of the ramp to the floor.
- Since the ball is projected
horizontally from the
edge of the ramp,
its initial vertical
velocity is zero.
- Its vertical
acceleration is just the 980
cm/second ^ 2 of
gravity.
- Knowing displacement, initial
velocity and acceleration we
use the equation represented
in the figure below.
- Since initial
velocity is 0,
the term v0 `dt will
be 0, which much
simplifies calculation
of `dt.
- We end up with the result
below.
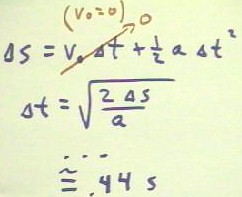
http://youtu.be/yZTWdd--xG4
We will continue this analysis at our next
meeting.
"
