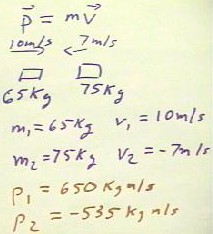Momentum; Projectiles; Problems

Class Notes Physics I, 9/30/98

Momentum; Projectiles; Problems

Questions on Assigned Problems

The equal and opposite forces exerted on two objects in a collision ensures that the change in the product m1 v1 of one is equal and opposite to the change in the product m2 v2 of the other. We call the product mv the momentum of an object. Since the momentum changes are equal and opposite we say that momentum is conserved. This statement can be extended to any number of interacting objects. This leads to the conservation of momentum equation m1 v1 + m2 v2 = m1 v1' + m2 v2' for objects of constant mass. Of the six quantities m1, m2, v1, v2, v1', v2' we can solve for one if we know the other 5, or if we know 4 of the other quantities and some relationship between them (e.g., that v1' and v2' are the same, or that the relative velocity of the two objects reverses upon collision: v2 - v1 = v1' - v2).

Momentum

When two objects collide they exert equal and opposite forces on one another, by Newton's third law.

If one object has a greater mass than the other, the magnitude of its acceleration will be less than that of the other, since the magnitudes of the forces on the objects are equal.
Its velocity will therefor change by less than that of the other, since the accelerations occur over the same time interval.

Thus in any collision the magnitude of the velocity change will be greater for the less massive object and less for the more massive object.

Consider the following question:

If a 65 kg football player running down the field at 10 m/second is met by a 75 kg football player running in the opposite direction at 7 m/second, then if the second player tackles the first head-on and holds on, will they move in the direction of the more massive player or in the direction of the player with the greater speed?

It is clear from the previous discussion that the magnitude of the velocity change will be greater for the 65 kg player then for the 75 kg player.
In order to reverse the direction of motion of the 65 kg player the magnitude of his velocity change must be greater than 10 m/second, while the 75 kg player will experience a change in direction of motion if the magnitude of his velocity change is greater than 7 m/second.
We could proceed along these lines and reason out the result. You should attempt to do so.

We could also follow our intuitive notion (expressed by several members of the class) that since mass and velocity both contribute to the 'effectiveness' of a mass in a collision, then this effectiveness might be measured by the product of mass and velocity.
In this case we might write p = mv, where p stands for what we call the momentum of the object.

We note that, as indicated by the arrows above the p and v in the figure below, momentum is a vector quantity just as velocity is, and that its direction is as important as its magnitude.
Thus when two objects are approaching head-on, the velocity and hence the momentum of one will be chosen to be positive, and these quantities will be negative for the other object.
In the present situation we will regard the direction of the 65 kg player as the positive direction.

The momentum of the first player is thus p1 = m1 * v1 = 65 kg * 10 m/s = 650 kg m/s.
The momentum of the second player will be p2 = m2 * v2 = 75 kg * -7 m/2 = -535 kg m/s.

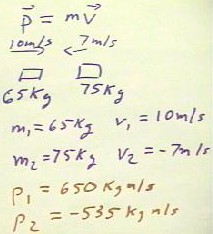
http://youtu.be/pO4jfqvcV1s

We thus have the situation as shown below, with a 650 kg m/second momentum approaching a -535 kg m/second momentum.

The total momentum in the situation is therefore the sum of these two momenta, or 115 kg m/s.

The impulse-momentum theorem tells us that the change in the momentum of an object is equal to the product of the force on the object and the time over which the force acts.

Since in this case the forces exerted in the collision are equal and opposite, it follows that the changes in momentum will be equal and opposite, so that the total momentum of the two objects will be unchanged in the collision.
Therefore, immediately after collision, we will have a total mass of 140 kg (recall that the players stay together for at least a short time after the collision), and this total mass will have the same total momentum they had before the collision.

Thus we will have a total mass of 140 kg with a momentum of p = mv = 115 kg m/second.
Since the mass is 140 kg, we thus have (140 kg) * v = 115 kg m/s, so v = .82 m/s.
Since this mass is positive, we see that the two players move in the direction of the first.
Though the first had less mass than the second, his greater velocity caused his momentum to dominate the collision.
This is not to say thay he gets hurt less than the larger player; remember that they both experience collision forces of the same magnitude, and all things being equal there forces will be more likely to injure the smaller player.

It is important to understand that this analysis concerns only what happens in the instants immediately before and after the collision.

The two players in fact come to rest, but this happens over the period of a second or so after the collision has occurred, and is the result mostly of the friction of the playing surface and perhaps the continuing efforts of the two players.
In the instant after collision, there is not enough time for either of these factors to have any effect.

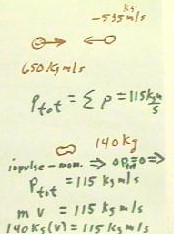
http://youtu.be/0maycU8MNLk

Quiz Problem

The quiz problem for today concerned a ball that slides down a ramp before being projected in the horizontal direction from the edge of the ramp and falling 1 meter to the floor.

Assuming that all the potential energy lost as the ball slides down the ramp is converted to kinetic energy, we are to determine horizontal range of the ball if the change in altitude of the sliding ball on the ramp is 1 cm, then 4 cm, then 16 cm.
Letting m stand for the mass of the ball, we see that for a 1 cm fall the change in potential energy is `dPE = m(980 cm/s^2) * (-1 cm).
The change in kinetic energy will be equal in magnitude and opposite to the change in potential energy, since by hypothesis the potential energy loss is compensated by the kinetic energy gain.
The resulting calculation is shown in the figure below.
Note that the mass m disappears when we solve for v; we obtain v = 44 cm/s.

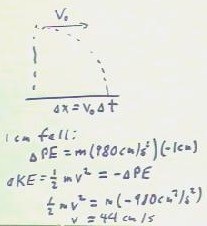
Similar calculations for altitude changes of 4 cm and 16 cm on the ramp yield the velocities indicated in the table below.

Since the vertical motion of the ball begins with velocity 0 (the initial velocity is in the horizontal direction so there is no vertical component) and accelerates toward the floor at 9.8 m/s^2 as it travels the 1 m to the floor, we have the vertical motion situation with v0 = 0, `ds = 1 m and a = 9.8 m/s/s.

We easily find that the time `dt required to reach the floor is .44 seconds.

We now apply our knowledge that the horizontal velocity does not change from the instant the ball leaves the edge of the ramp to the instant it strikes the floor, we see that for the 1 cm vertical slide, with the resulting 44 cm/s horizontal velocity, the horizontal displacement must be `ds = 44 cm/s * .44 s = 20 cm.

The horizontal displacements for the other two situations are calculated in the same manner.
We will obtain displacements of approximately 40 cm and 80 cm.

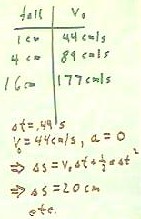
http://youtu.be/J0Gi9fPzoqI

It is important to understand that the ball undergoes at least two phases of motion in this situation.

The first phase is the slide down the ramp, and no assumption is made as to whether the ramp as a uniform slope or not.
During this phase, then, the acceleration may be either uniform or nonuniform; since the only thing that matters here is the velocity the ball attains, we can determine this result by energy considerations and it doesn't matter whether the acceleration is uniform or not.

The second phase begins at the instant the ball leaves the edge of the ramp and ends at the instant it strikes the floor.

Between these two instants the acceleration of the ball is completely uniform (provided we ignore the negligible contributions of air resistance and other very small forces), with a horizontal acceleration of 0 and a downward vertical acceleration of 9.8 m/second/second.

At the instant the ball strikes the floor a third phase begins, but we are not concerned with this phase at this time. Our attention is focused mainly on the second phase, with the first phase relevant only because it contributes the initial velocity for the second.

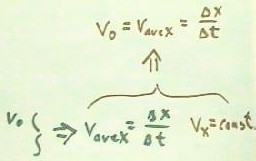
The general situation is depicted below.

`dy is the vertical displacement of the ball has its slides down the ramp, v0 is the horizontal velocity attained by the ball as result of its slide down the ramp, `dh is the vertical distance which the ball falls, and `dx is the horizontal range of the ball.

As we have seen before,

v0 is proportional to `sqrt(`dy) because of energy considerations,

`dx seems also to be proportional to `sqrt(`dy) as indicated by our experimental analysis, so that

v0 is proportional to `dx.

We also saw by flicking one washer off the horizontal edge of a table and dropping another at the same instant that the time of fall `dt appears to be independent of the horizontal velocity of the falling object.

It follows that the horizontal range `dx is always equal to the product of the average horizontal velocity vAvex and the uniform time interval `dt:

`dx = vAvex * `dt, where `dt is the same for every initial velocity.

If the x velocity is indeed constant, then for each situation vAvex will be equal to the initial velocity v0 for that situation, and we will have v0 = `dx / `dt.

We can validate these assumptions by directly observing the velocities attained by the ball on various ramps and comparing with the observed ranges `dx and the calculated time interval `dt.
Our results will confirm the hypothesis that the x velocity is in fact constant.

http://youtu.be/j6dcZd7XAeM

Questions on Assigned Problems

The following question was posed by a student:

For the problem where an automobile stops from a speed of 90 kilometers/hour in a distance of 50 m, it is clear that the initial velocity will be v0 = 90 km/hr = 25 m/s, the final velocity will be zero and the displacement will be `ds = 50 m.
It is also clear that in order to determine the acceleration we will use the equation vf^2 = v0^2 + 2 a `ds, in which all the quantities except a are known.
The question is, how do you do the algebra to solve this equation for a?

As shown below, we need to isolate a, and we begin doing so by adding -v0^2 to both sides of the equation.

This isolates 2 a `ds on one side of the equation.

Note that we could have begun by multiplying both sides by the reciprocal 1 / (2 `ds), which would also in a sense have isolated a, but to do so we would have had the multiply both vf^2 and v0^2 by the same factor and this would have complicated the algebra unnecessarily.

Usually in a situation like this we perform additions before we get into multiplications, in order to keep the algebra as simple as possible.

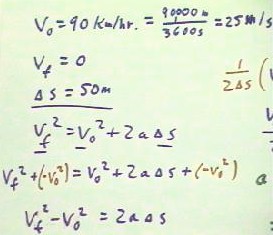
The next step will be to multiply by the reciprocal 1 / (2 `ds) of the coefficient of a, thus obtaining a = (vf^2 - v0^2) / (2 `ds).

We then substitute the known initial and final velocities and the displacement, and simplify our expression to obtain the acceleration shown below.
Note that in the first substitution step we have effectively used (-v0^2 + vf^2) / (2 `ds) instead of (vf^2 - v0^2) / (2 `ds); that was an instructor error of form, though it is mathematically correct.

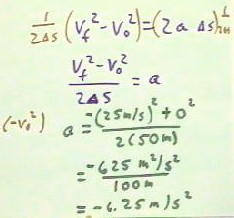
http://youtu.be/Q3UjuJWvf0I

Another question was posed to in relation to the problem of a sprinter who accelerates uniformly (which is unrealistic, incidentally) from 0 to 11.5 m/second while covering a distance of 15 m.

The individual posing the question noted that we have v0, vf and `ds.

We might begin by constructing a flow diagram for this problem.
Given v0, vf and `ds, we first note that from v0 and vf we can easily determine vAve and `dv.
We can then use our value of vAve along with our given value of `ds to determine the time interval `dt over which the acceleration occurs.
We can then combine our knowledge of `dt with our knowledge of the velocity change `dv to obtain the acceleration.

vAve is obtained as the average of initial and final velocities, vAve = (v0 + vf) / 2, and in this case is 5.75 m/s.

Since the displacement is `ds = vAve `dt, we see that `dt = `ds / vAve; substituting the known values we obtain `dt = 2.7 sec.
Since the change in velocity is the difference between initial and final velocities, `dv = 11.5 m/s, we are now in a position to easily obtain the acceleration a = `dv / `dt = 11.5 m/s / 2.7 sec = 4.3 m/s/s.

http://youtu.be/iU-c7UQGvaQ