Projectiles; Impulse-Momentum Theorem

Class Notes Physics I, 10/05/98

Projectiles; Impulse-Momentum Theorem

Quiz Problems

Today's quiz problems involved projectiles projected in the horizontal direction from the edge of a table 80 cm above the level floor.

In the first problem, as depicted below, we are given that the initial x velocity is 70 cm per second and we are asked to find the horizontal range `dx of the projectile.

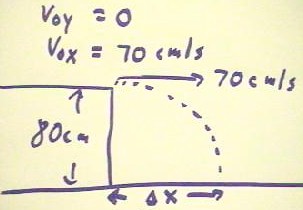
In any projectile problem we completely separate the horizontal and vertical motion, and in general or first goal is to find the time interval `dt.

In this case we find `dt from our knowledge of the vertical initial velocity, displacement and acceleration.
Since the object is projected in the horizontal direction, its initial vertical velocity must be 0.
Its vertical displacement is 80 cm (where the downward direction has implicitly been chosen as the positive direction) and its acceleration is 980 cm/s^2.
Using these quantities we easily determine that `dt = .4 sec.

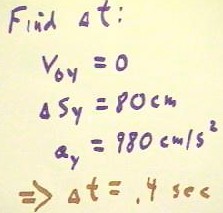
With this value of `dt we can now easily solve the horizontal motion problem.

We know that the horizontal acceleration is 0, we know the horizontal initial velocity and we know `dt, so we could use one of the four fundamental equations of uniformly accelerated motion. However, we choose instead to simply reason out the answer. We know that in a projectile problem, where not otherwise stated, the horizontal velocity is constant. Moving a constant velocity of 70 cm/s for .4 sec we will move 28 cm, so the horizontal range is `dx = 28 cm. Details are shown below.

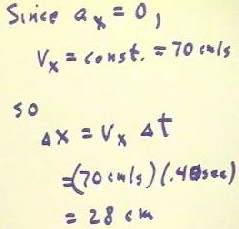
http://youtu.be/UMKQSjSpwlo

The alternative quiz problem specified a horizontal range of 70 cm, with the initial velocity in the horizontal direction and a fall of 80 cm. In this case we are asked to find the initial horizontal velocity.

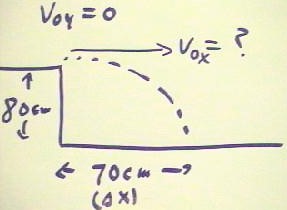
We again easily determine from the vertical motion that `dt = .4 sec. Then, knowing that vx is constant, and therefore equal to vAve, we see that vx = `dsX / `dt = 70 cm / (.4 sec) = 175 cm/s.

http://youtu.be/_TaX_2ky_KQ

A related problem gives the initial x velocity and horizontal range of a projectile projected in horizontal direction and asks for the height of the platform from which the projectile was projected.

In the present example we have an initial horizontal velocity of 50 cm per second and horizontal range of 250 cm.

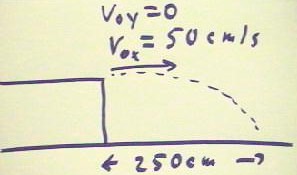
We can directly reason out the vertical motion of this projectile.

We could also use the equations of uniformly accelerated motion, but direct reasoning is preferable because it brings us closer to the essential nature of the problem and the basic ideas upon which we base our analysis of uniformly accelerated motion. In general we should always attempt to reason out our results directly before we reach for an equation.
We should then use the equations of motion to check our results and further deepen our understanding.

As usual we began by attempting to find `dt.

Looking at the horizontal motion we immediately see that if we move 250 cm at a constant velocity of 50 cm/second, the basic idea of velocity tells us that `dt = 5 sec (i.e., moving in 50 cm increments every second we move 250 cm in 5 such increments; we visualize 1 second's displacement and ask how many such displacements it takes to move through the given displacement).

We then apply our knowledge of `dt to the vertical motion.

Accelerating at 9.8 m/sec./second for five seconds, velocity must change by 49 m/s (we visualize or speedometer changing by 9.8 m/second every second for five seconds).
Since initial velocity is 0 this implies a final velocity of 49 m/second and therefore an average velocity of 24.5 m/second.

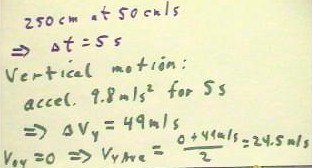
Moving at an average horizontal velocity of 24.5 m/sec. for 5 sec., we clearly move a horizontal distance of 5 * 24.5 meters = 122.5 m.

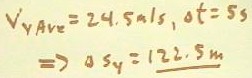
http://youtu.be/pZjGP0hnDDs

Question Concerning Text Problem

A question was asked about a situation in which a car moving at some constant velocity stops in response to some emergency.

The driver has a reaction time of one second, and acceleration of the car is given.
We are asked to find a total distance required to stop the car.

The individual who posed the question recognized that we have two motion phases, one lasting one second at the initial velocity and the other characterized by acceleration from the initial velocity to final velocity 0, and that for the second phase we would use the equation vf^2 = v0^2 + 2 a `ds to determine the displacement. The question regarded the algebra required to solve the equation.

If we assume an initial velocity of 35 m/second, and an acceleration of -.5 m/sec./second, then we identify v0 as 35 m/s, vf as 0 and a as -.5 m/s/s.

We note that the equation vf^2 = v0^2 + 2 a `ds contains known quantities a, vf and v0 (underlined) and the desired variable `ds.

We will solve the equation for `ds.

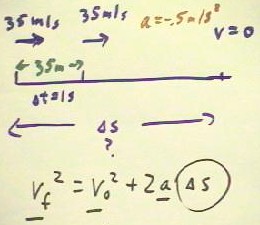
The solution is similar to that illustrated in the 9/30 lecture, where we solved the same equation for a.

As then, we add -v0^2 to both sides then multiply both sides by the reciprocal of the coefficient of the variable for which we are solving.
In this case to variable is `ds and its coefficient is 2a, so we will add -v0^2 to both sides and then multiply both sides of the resulting equation by 1/ (2a), obtaining `ds = (vf^2 - v0^2) / (2a).
We then substitute the values of the variables and easily quickly find the result, `ds = 1225 m.
The total stopping distance will be found by adding the 1225 m to the 35 m traveled during the reaction time.

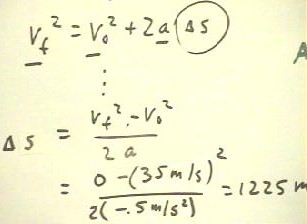
We could have reasoned out the 1225 m distance easily enough, as follows:

To come to stop from 35 m/second requires a velocity change of negative 35 m/second.
At -.5 m/s it should be clear that this will require 70 seconds.
It should also be clear that our average velocity will be 17.5 m/s, so that in the 70 seconds we will travel total distance of (17.5 m)(70 s) = 1225 m.

http://youtu.be/dFQ54h27bPQ

The Impulse-Momentum Theorem

Recall that if we take the two equations of uniformly accelerated motion

vf = v0 + a `dt and vf^2 = v0^2 + 2 a `ds,

and combine them with Newton's Second Law in the form a = F / m, where F is the net force acting on an object of mass m, we obtain the equations

vf = v0 + (F/m) `dt and vf^2 = v0^2 + 2 (F/m) `ds,

as indicated in the figurebelow.

Recall that when we solve the second equation for the quantity F `ds, circled in red, we obtain the work-energy theorem

F `ds = .5 m vf^2 - .5 m v0^2, or

`dW = .5 m vf^2 - .5 m v0^2 = KEf - KE0 (where `dW is the work done by the net force F).

When we solve the first equation for F `dt, we obtain F `dt = m vf - m v0.

Since we have defined momentum to be p = mv, we see that the right-hand side is just the change pf - p0 in the momentum of the object, so that F `dt = `dp.
We call the quantity F `dt the impulse of the force.

Recall that the distinction between F `dt and F `ds is illustrated in the apparent contradiction between the fact that an object moving a given distance down a given incline experiences the same force and therefore the same acceleration over that distance whatever its initial velocity, although we observe that it experiences less of a velocity change when initial velocity is higher.

This apparent contradiction is resolved when we realize that it is the product F `ds that is the same for all initial velocities, but that this product (the work) is associated with a change in v^2 (associated with KE).
The change in v (proportional to the momentum) is associated with the product F `dt (the impulse).
Since on the incline `dt is less for greater initial velocity, there will be less impulse F `dt and hence less change in momentum mv and less change in v.

http://youtu.be/o9HFAdISnk4

It is not always the case that the force acting on object is constant.

Typically in a collision the force starts at 0 when the colliding objects first make contact, increases to some maximum Fmax, then decreases to 0 again.

The change in force with clock time is usually not linear, but we first postulate a linear change from 0 to Fmax and back to 0.

We wish to determine what the impulse of such a variable force might be.

Since the impulse of constant force is F `dt, the impulse of a force which changes linearly from 0 to Fmax might be thought of as the product of the average force Fave and `dt.

Since the average force in the case of a linear change would be (0 + Fmax) / 2 = 1/2 Fmax, we see that the average force in the situation below must be 1/2 Fmax (the preceding argument clearly applies just as well when the force decreases from Fmax to 0).
The impulse of the force shown in the figure below therefore should be 1/2 Fmax * `dt.
We note that this impulse is therefore equal to the area under the force v. clock time graph.

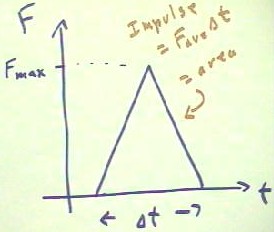
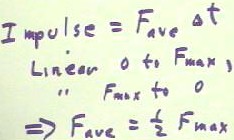
A more realistic F vs. t graph is shown below.

The dotted lines represent a linear increase from F = 0 to Fmax, then a linear decrease back to 0.
It should be clear that the areas beneath the two graphs are approximately equal, and that we can still therefore assume that the average force is Fave = 1/2 Fmax and the impulse is 1/2 Fmax `dt.

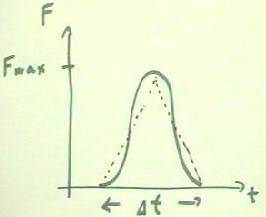
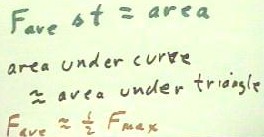
Phy 241 students should note that the impulse of a force is simply the integral of that force with respect to time, represented by the area under the force vs. clock time graph.

http://youtu.be/0SNZjLQtpaw