"
Class Notes Physics I, 10/07/98
Momentum in Two Dimensions
The quiz problem involved to masses approaching each other and colliding head-on, after
which they stick together and move off as one object.
- The first object has a mass of 5 kg and is originally moving at 10 m/second in a
direction we will regard is positive.
- The second has a mass of 5 kg and an unknown velocity before collision.
- It is known that the velocity after collision is 2 m/s in the direction of the second
object.
- We wish to determine the velocity of the second object before collision.
We set the problem up as shown below.
- We will use v to stand for the
unknown velocity of the 5 kg mass before collision.
- Since the velocity of the combined
mass after collision is in the original direction of motion of the second mass, which is
opposite to the (positive) original direction of the first mass, its velocity will be -2
m/s.

In symbols, using v1B and v2B for the velocities of the two masses before collision and
pTotB and pTotA for the total momentum before collision and after collision we have m1 =
m2 = 5 kg, v1B = 10 m/s and v2B = v so that the total momentum before collision is
- pTotB = 5 kg * 10 m/s + 5 kg * v = 50 kg m/s + 5 kg * v.
After collision we have a mass of 10 kg moving at velocity -2 m/second, so the total
momentum is
- pTotA = 10 kg * (-2 m/s) = - 20 kg m/s.
The known momenta are the 50 kg m/s of the first object before collision and the -20 kg
m/second total momentum after collision.
- The -70 kg difference is accounted
for as the momentum of the second object before collision.
- That is, since the total momentum
before collision must equal the total momentum after collision, we see that the momentum
of the second object before collision must be -70 kg m/s.
- From this we can easily conclude
that the second object has a velocity of -14 m/s before collision.
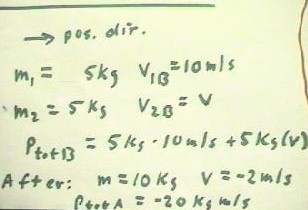
Proceeding a bit more formally, we set up the equation with the total momentum before
collision set equal to the total momentum after collision.
- We easily solve this equation for
the unknown velocity v of the first object before collision, obtaining v = -14 m/s.
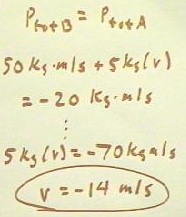
The numerical reasoning used above allows us to visualize the actual quantities
involved in the situation.
We can generalize this reasoning by using symbols, as shown below.
- Using vA before the velocity of the combined object after collision, the conservation of
momentum in this collision is expressed in the equation shown below
- The left-hand side stands for the total momentum before collision and the right-hand
side for the total momentum after collision.
- The equation represents the equality of the total momentum before collision and that
after.
We can solve this equation for v2B, the unknown velocity of the second object before
collision.
- The numerator of the resulting
expression is the difference between the total momentum after collision and the momentum
of the first object before collision, which represents the momentum of the second object
before collision.
- The denominator, which is the mass
of the second object, shows that we divide the total momentum of the second object by its
mass to obtain its velocity.
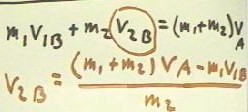
http://youtu.be/Or0FCzUvQ3Q
Momentum in Two Dimensions
If we collide two metal balls in such a way that the collision is not quite head-on,
they will both change direction, and we will no longer be able to model the situation by
motion along a single axis.
- We will therefore model this situation in two dimensions, using x and y components of
velocity and momentum.
- Since we can no longer indicate the direction of motion by + or -, as we could when the
motion was all along a single axis, we will have to use vectors to express velocities and
momenta.
- In this situation, where motion has components in the x and in the y directions, a
velocity or momentum vector will have both x and y components.
- A velocity vector v (note that vectors will be indicated by bold-faced
symbols, or alternatively by symbols with small arrows above them as below) will have
components vx and vy in the x and y directions.
A momentum vector p will similarly have x and y components px and py.
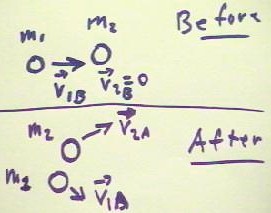
The situation in which a moving ball collides with a stationary ball is depicted below.
- The collision is such that the
moving ball strikes the stationary ball to the right of center of the stationary ball, as
it would be observed from the moving ball.
- After collision the moving ball's
velocity will be deflected to the right and that of the stationary ball will be deflected
to the left.
- The forward velocity of the first
ball will be reduced as a result of the increased forward velocity of the second.
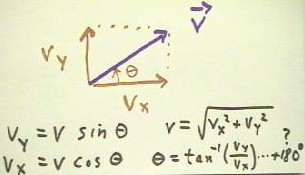
The geometric relationship among vx, vy and v is depicted by a
rectangle formed by side of lengths vx and vy originating at a common point and pointing
in the x and y directions, with the vector v representing the velocity
running diagonally from the common point to the opposite diagonal of the rectangle.
- The rectangle is completed by
dotted lines parallel to the x and y axes, running from the point of v to
the points of vy and vx.
- These dotted lines are called
projection lines.
- (Note that in the figure as shown
below the shape of the rectangle has been somewhat distorted by a combination of camera
angle and poor artwork on the part of the instructor; the angles between the projection
lines and the component vectors vx and vy should be right angles).
From the geometric relationships and the definitions of the sine and cosine functions,
we can see how the components vx and vy are related to the magnitude and angle of the
vector v.
- A velocity vector v,
representing motion in a direction which makes an angle `theta with respect to the
positive x axis, will have x component vx = v cos(`theta) and y component
vy = v sin(`theta), where the non-boldfaced v (or v without an arrow
above it) stands for the magnitude of the velocity, or the speed, of the object.
- If the x and the y components of
the velocity are known, then the magnitude v of the velocity is found by the Pythagorean
Theorem to be v = `sqrt(vx^2 + vy^2) and the angle with respect to the x
axis is `theta = tan^-1(vy / vx) or tan^-1(vy / vx) + 180 deg, depending
on whether vx is positive or negative, respectively.
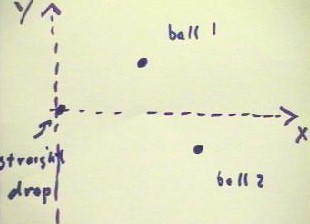
If we collide the two balls near the edge of a table of known height, so that their x
and y velocities can be inferred from the x and y displacements of their landing locations
with respect to the location of a straight drop from the point of collision (more
specifically, from the location of the center of mass of the two balls at the instant of
collision), we will obtain a picture like the one below.
- Here the x and y axes are both in
the plane of the floor (this means that we are not regarding the vertical direction as the
y direction; we might now regard the vertical direction as the z direction).
http://youtu.be/uJWU-xdi6UU
http://youtu.be/8YvFkhdjjdM
Knowing the z displacement from the edge of the table to the floor, we can easily infer
the time required to fall through that displacement from rest (we assume that we have
taken care that the vertical, or z velocities of the balls are 0 immediately after
collision).
- Then by measuring the x and y
displacements of the balls from the straight-drop position we can easily determine the x
and y velocities of the balls immediately after collision.
If we know the masses of the balls, we can now easily find their momentum components
p1x, p1y, p2x and p2y after collision.
- If the direction of the first ball
before collision is taken as the x direction, we see that before collision that total
momentum in the y direction was zero.
- It must follow that the total y
momentum after collision must also be 0, so that p1y and p2y are equal and opposite.
- The total p1x + p2x of the momenta
after collision must be equal to the momentum of the first ball before collision.

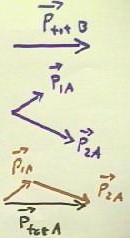
From the x and y components of the momenta after collision, we can find the magnitude
and direction of the momentum vectors p1A and p2A after
collision.
- These momenta can be expressed by
the vectors p1A and p2A, as they might be depicted in
the figure below.
- The total momentum after collision
can be depicted by the sum of the two vectors, depicted by placing the vectors
head-to-tail as shown below.
The total momentum after
collision will be the vector originating at the 'tail' of the first vector and ending at
the 'head' of the second.
- This total momentum should be
equal to the total momentum pTotB before collision, which is completely
in the x direction, as depicted by the vector pTotB in the figure below.
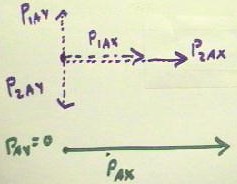
A more detailed sketch of the vector sum shows the components p1Ax, p1Ay, p2Ax and p2Ay
of the two momenta after collision.
- Since the total momentum after
collision should be zero, the y components should be equal and opposite.
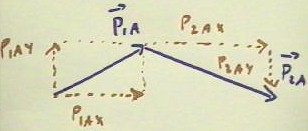
The process of adding the x and y components is represented below, with the x and y
component vectors all originating from the same point.
- This picture shows how the y
components are equal and opposite and hence cancel (e.g., if instead of momentum
components we imagine two equal and opposite force components acting on the same point, it
is clear that neither force will win and that the net result will be 0).
- The x components of the momentum
are in the same direction and hence reinforce one another, resulting in a total x
component which is greater than either.
- The sum of these x components is
depicted by the green vector below (this vector should have been drawn longer; its length
should be equal to the sum of the lengths of p1xA and p2xA).
http://youtu.be/e7kTfAJi7rY
"
