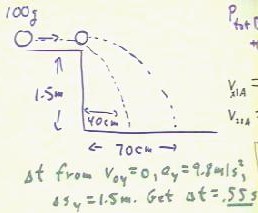More Momentum; Impulse-Momentum

Class Notes Physics I, 10/09/98

More Momentum; Impulse-Momentum

The figure below depicts a familiar lab situation: A 100 g mass is rolling at 90 cm/second toward a stationary object of unknown mass.

After collision it is observed that both balls leave the edge of the table moving in the horizontal direction.
Measurement shows that the 100 g mass travels 40 cm in the horizontal direction from the point of collision as it falls 1.5 meters to the floor, while the unknown mass travels 70 cm as it falls the same distance to the floor.
From this information we are to determine the mass of the second ball.

We can immediately determine the time required for each ball to fall to the floor.

Each ball is a projectile with an initial vertical velocity of 0, accelerating the distance of 1.5 meters at 9.8 meters/second/second.

The time required is easily calculated to be `dt = .55 seconds.

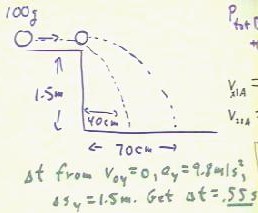
Using this `dt we can easily determine from the horizontal distance traveled by each ball, and by the fact that horizontal velocity doesn't change, that immediately after collision the balls have horizontal velocities v1x = 40 cm / .55 sec = 73 cm/sec and v2x = 70 cm / .55 sec = 127 cm/sec.

We also note that just before collision that total momentum of the system consisting of the two balls is pTotBefore = 100g * 90 cm/s + m2 * 0 m/s = 9000 g cm / sec, where m2 stands for the unknown mass of the second ball.
Total momentum after collision is found just as easily, using the two after-collision velocities obtained above.
This total is pTotAfter = (100 g)(73 cm/sec) + m2 (127 cm/sec) = 7300 g cm/sec + m2 * 127 cm/sec.

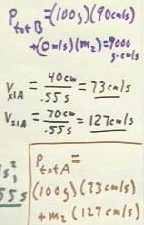
http://youtu.be/mui1zEGvUAc

Knowing that total momentum must be the same before as after the collision, and noticing that the momentum of the first ball decreases by 1700 g cm/second, we could conclude that the momentum of the second ball must increase by 1700 g cm/second.

Since that ball started from velocity 0, we could easily find its mass from its now-known velocity after collision and this momentum change. You should do this.

Alternatively, and more formally, we could set the two expressions for the total momentum before and after collision equal and solve for the unknown mass m2.

This equation is written below, and as shown is easily solved to obtain m2 = 13.4 grams.

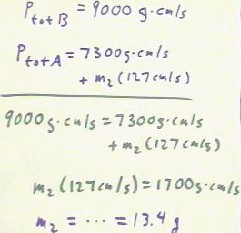
http://youtu.be/EIsSwfhcqBo

At this point the instructor made a serious mistake, and should have known better but just wasn't very alert.

The known quantities were underlined and the unknown quantities were circled.

Note that m2, which is certainly unknown in the situation we have just analyze, was circled on the left-hand side and underlined on the right-hand side.

This error compounded itself in interesting ways as the instructor 'solved' the equation for m2. Believing that the only representation of the unknown quantity was the circled one, the instructor proceeded to isolate this variable by subtracting m1v1 from both sides of the equation, then dividing by v2.

Caught up in the elegance of the algebra, the instructor then proceeded to factor m1 out of two terms in the numerator to get what appeared to be the final result, not noticing that m2 was still present in the numerator of the right-hand side so that all this amusing algebra had failed to produce a solution for m2.

The correct solution would have involved subtracting m1v1 and m2v2' from both sides, placing the unknown mass m2 solely on the left-hand side of the resulting equation m2 v2 - m2' v2' = m1 v1' - m1 v1.

Factoring m2 out of the left-hand side and m1 out of the right-hand side, the equation would become m2(v2 - v2') = m1 (v1' - v1).

Another simple step and the solution m2 = m1 (v1'- v1) / (v2 - v2') would have been obtained.

Noting that the change in the velocity of the first object is in fact `dv1 = v1' - v1, while the change in the velocity of the second is `dv2 = v2 - v2' = -(v2' - v2), we see that m2 = m1 (`dv1 / (-`dv2) ).

Thus we have `dv1 / `dv2 = -m2 / m1: The ratio of the velocity changes is the negative reciprocal of the mass ratio.

This shows that the greater mass has a proportionally smaller change in speed.

We also see that the velocity changes are in opposite directions.

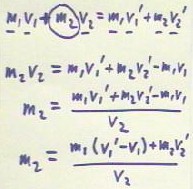
http://youtu.be/c_ILhaSO5FA

In the preceding example the second object had a change of momentum equal to 1700 grams cm/second.

If the collision occurred in .01 seconds, we might ask what average force was exerted during the collision.
We can find the average force by using the impulse-momentum theorem, which says that the impulse Fave * `dt is equal to the change `dp in the momentum of the object.

In this case, `dp = 1700 g cm/sec, and `dt = .01 sec.

Solving the equation Fave `dt = `dp for Fave, we obtain Fave = `dp / `dt.

Substituting the known values of `dp and `dt, we see that Fave = 170,000 g cm / s^2.

In standard MKS units, since it takes 1,000 grams to make a kilogram and 100 cm to make a meter, this average force would be expressed as 1.7 Kg m /s^2 = 17 Newtons.

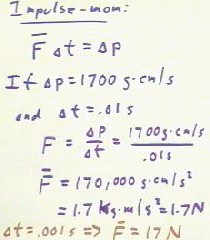
http://youtu.be/ZZ8Mm0sBR0o