Orbit Simulation

Class Notes Physics I, 11/02/98

Orbit Simulation

The Orbit Simulation Program GRVFIELD

Before you run the orbit simulation program on your computer, make careful note of the following: IT IS POSSIBLE THAT THE PROGRAM CAN ONLY BE STOPPED BY HOLDING DOWN THE CRTL KEY AND STRIKING THE PAUSE/BREAK KEY AT A PROMPT. THIS GLITCH WILL BE FIXED AS SOON AS POSSIBLE, BUT IN THE MEANTIME BE WARNED.

The orbit simulation program (see the homepage under DOS simulations to download; the program is named GRVFIELD, and is run by simply double-clicking on its name in Explorer) simulates the motion of a satellite around the planet of your choice. To choose a planet you need only specify

the planet's radius (as a multiple of Earth radius: e.g., if a planet has three times the Earth radius you would enter 3), and
the strength of the gravitational field at its surface (the strength of a gravitational field is measured in m/s^2, and is equal to the acceleration of gravity at the surface).

The first thing the program will do is plot out the locations of the spheres where the strength of the gravitational field takes values of 95%, 90%, 85%, ..., 5% that of the surface value.

These spheres are called 'equipotential' spheres; if you work to climb from the surface of the Earth to one of the spheres (assuming a sufficiently high tower with an appropriate atmosphere and climbing holds), it wouldn't matter to what point on the sphere you climbed, your potential energy increase would be the same.

This is why the spheres are called equipotential surfaces.

On each equipotential surface two imaginary spheres are drawn to represent the strength of the gravitational field at that surface. The strength is indicated by the volume of the spheres, which as you know is proportional to the cube of their diameter (e.g., a sphere with twice the diameter of another has eight times the volume). So imagine that the force is contained in the round balls indicated on each equipotential surface.

From each sphere a line is drawn to the center of the planet, indicating that the direction of the gravitational field at every point is toward the center of the planet.

Whatever option you choose, the surface of the planet will be indicated by a red ring.

When you do an orbital simulation it will not stop when the satellite strikes the surface of the planet; this would be depressing.
So the simulation thinks that the planet has been compressed into a black hole, and the red ring simply represents the original radius of the planet before he was compressed.
It isn't clear why the program doesn't find this depressing, considering the likely fate of any life on the surface of the planet as it is compressed.

The program provides you with two options for how many equipotential lines to plot.

It will either plot lines down to the surface of the planet, at intervals of 5% of the field strength at the planet surface, or it will plot the lines as they would be if the planet shrank to a black hole, continuing until the gravitational field strength is 10 times that at the surface.
The program will either plot the circles representing these surfaces without your intervention, or it will wait for you to strike the Enter key between surfaces; you will be prompted to choose.

You can choose to either run the orbits as quickly as your computer will allow (the default speed is set for a 386 computer; a fast Pentium will be on the order of 100 times faster, and may require a time interval between .001 and .01 seconds to plot an orbit slowly enough for you to think about what is happening. If you just want to see the shape of the orbit you can run the simulation at top speed).

After the equipotential surfaces are plotted, you will be prompted to begin an orbital simulation. You will be first asked for the maximum runtime of the simulation, in seconds.

There is no way to stop the simulation once it starts, so don't tell it to run for 47 million years or you won't be able to shut down your computer until that time has elapsed (actually, you can use CTRL-ALT-DEL to shut down any program, but this is something you want to avoid).

You will then be asked for the initial distance of the satellite from the planet, as a multiple of the radius of the planet.

For example, if you tell the program that the initial distance should be 1.4, then the radius of the orbit will be 1.4 times that of the planet.

Having specified the initial distance of the satellite from the planet, you'll have to tell the program what the angular position of the initial position is.

To encourage you to think in radians, angular positions will be in radians, as measured counterclockwise from the positive x axis.

(As a default if you don't know what angle you want to use, tell it 0; then learn enough about radians to place the satellite wherever you wish).

You'll next be asked for the initial speed of the satellite, in m/s.

For low-Earth orbit, here is a hint: the initial speed is between 5,000 and 10,000 m/second.

Your first exercise will be to find the speed using the simulation.

Note on accuracy: The simulation is not completely accurate.

Orbits are plotted more accurately for shorter time intervals.

For default time intervals, the orbits won't quite close on themselves -- i.e., they won't come back exactly to their starting point. This is because the simulation was written to work on pretty slow computers.

If you choose short time intervals, accuracy will be very good. Even at the default accuracy, however, the velocities and paths of circular orbits of Earth are more than 99% accurate.

You will then be asked for the initial direction of the satellite's velocity, again in radians.

To achieve a circular orbit, in the cases where this is your goal, you should recall from geometry that a tangent line to a circle is perpendicular to a radial line.

If you are using defaults, it is possible to achieve a circular orbit with an initial angular position of 0 and a velocity in the direction `pi / 2, which is approximately 1.57 radians. Note that you must give all numbers in decimal form.

After you have given the program this information, it will run the simulation.

When the simulation tends, you will be asked again for the runtime.
If you enter 999 for the runtime, you will be taken back to the beginning of the program so you can change any of the parameters you wish.
Otherwise you can change the initial position and velocity, as well as the runtime for the simulation, to achieve whenever goal you presently have.

The following series of exercise is strongly suggested:

Determine the velocity required to achieve a perfect circular orbit of Earth at distances of 1, 1.5, 2 and 2.5 times the radius of the Earth. Plot these velocities vs. distance from the center of the Earth to see if they are linear with respect to distance, or if they increase at an increasing or decreasing rate.
Determine the maximum distance a satellite can move from the surface of the Earth if it is 'shot' radially away along a line from the center of the Earth at velocities of 1000, 2000, 3000, . . . m/s. Plot maximum distance against initial velocity. Plot maximum distance and against initial kinetic energy. Speculate on what the graphs are telling you. (Note: don't take any distances seriously that appear to occur after the satellite crashes into the center of the Earth; the program seems to have a perverse sense of humor about such things; or maybe it knows things that we don't about what happens when satellites crash into black holes).

Notes on Radian Measure

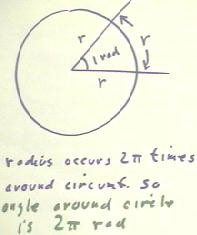
Definition of the Radian: A radian is an angle such that the arc on a circle intercepted by the angle has arc length equal to the radius of the circle. Sort of like an equilateral triangle; the angle is slightly less than 60 degrees.

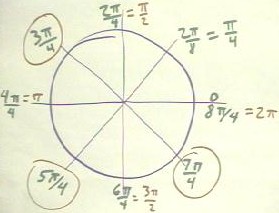
We can list angles in multiples of `pi / 4, which is 1/8 of 2 `pi radians, corresponding to 1/8 of 360 deg or 45 deg. We list `pi/4, 2`pi/4, 3`pi/4, 4`pi/4, etc., then we reduce the fractions where possible. You should carry this picture, and the one below, in you head; you should draw it daily until its logic is firmly part of your worldview.

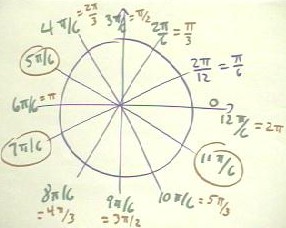
Here we list, in a manner similar to that above, the multiples of `pi/6, which corresponds to 1/12 of 2 `pi, or 1/12 of 360 deg, or 30 deg.

http://youtu.be/0F3AcYNVFVE

Some velocity estimates made by VHCC in-class students using the simulation program:

http://youtu.be/iWUyAwAO9V4

http://youtu.be/uYBE5eAecOQm

http://youtu.be/P8grjXD8zlI

As we will see later, for circular orbits the orbital velocity is inversely proportional to `sqrt(r), where r is orbital radius.