"
Class Notes Physics I, 11/04/98
Orbital Velocity, Energies
Today's quiz problem was to determine what velocity of a circular orbit would be
consistent with a centripetal acceleration equal to the gravitational force at a distance
of 500 kilometers above the earth.
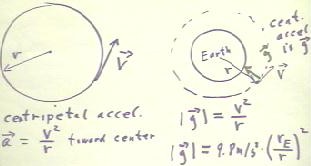
The centripetal acceleration for an object moving in a circle of radius r is
known to be v2 / r.
- An orbit 500 kilometers above the earth will have a radius 500 kilometers greater than
that of the earth.
- Since the radius of the earth is approximately 6.4 * 10 ^ 6 m, the orbit will have
radius r = 6.9 * 10 ^ 6 m.
- The strength of the gravitational field at this radius is 9.8 m/s2 * (rE / r)
2 = 9.8 m/s2 * (6.4 * 10^6 m / (6.9 * 10^6 m))2 = 8.6 m/s2
(verify this result, which might be slightly inaccurate).
We therefore see that, if v2 / r = g(r), r = `sqrt( r * g(r) ) = `sqrt(6.9 *
10^6 m * 8.6 m/s2) = 7600 m/s (again verify this unvalidated result).
To show that the acceleration of an object moving in a circle is directed toward the
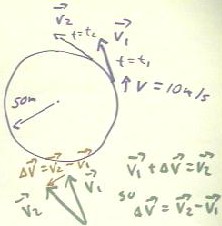
center of the circle, we consider to velocity vectors v1 and v2,
corresponding to clock times t1 and t2, for an object moving
constant speed around a circle.
- Since average acceleration is
defined as `dv / `dt, it is clear that since the two velocities are represented by
different vectors, there is a nonzero difference `dv and therefore a nonzero average
acceleration between the two clock times.
- This is consistent with our
experience that when we move in a circular path, something must exert a force to keep us
in that path (e.g., the door against which we might be leaning as some fool drives the car
in which we are riding almost too fast around a curve). (Our experience that an object
hanging by a string from the ceiling of our car will be displaced in a direction opposite
to that of the curve, and perpendicular to the curve, provides further evidence; the
tension component in the string provides the force necessary to keep the object moving in
the circle; without that force the object would continue moving in a straight line).
We now consider the two vectors v1 and v2.
- If we draw the vectors with a
common point of origin we can see that the vector labeled `dv in the figure below,
originating at the terminal point of v1 and terminating at the terminal point
of v2, has the property that v1 + `dv = v2.
- From this we easily conclude that
`dv = v2- v1, so that it certainly does indicate the difference in
the velocities.
We note also that the three vectors v1, v2and `dv form an
isosceles triangle, since v1 and v2 have the same magnitude.
- We note that `dv therefore makes
the same angle with both v1 and v2, and the fact that the angles of
the triangle formed by these vectors at up to 180 degrees.
- We conclude that as `dt = t2-
t1 gets closer and closer to zero, the approach of the apex angle of the
triangle to 0 implies that the angle between `dv and v1 or v2
approaches 90 degrees.
We can also determine that `dv /
`dt is approximately equal in magnitude to v2 / r, with the approximation
approaching v2 / r as a limit as `dt approaches zero.
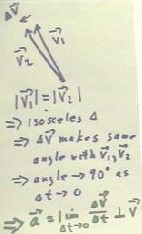
Video file #01
We generalize the quiz problem in the figure below.
- We note that for a circular orbit the centripetal acceleration v2 / r is
equal to the gravitational field strength g = 9.8 m/s2 * (rE / r) 2
at distance r from the center of the earth.
Setting the two quantities equal we easily solve for v, obtaining v = `sqrt( 9.8 m/s2
* rE2 / r).
- The quantity `sqrt(9.8 m/s2 * rE2) = `sqrt(9.8 m/s2) *
rE is approximately 2 * 10^7 m3/2 / s, so we could write v = k / r, with k = 2
* 10^7 m3/2 / s (approximately; you should calculate this constant with an
accuracy of at least three significant figures).
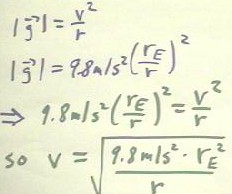
Video file #02
We note that the velocities obtained from v = `sqrt( 9.8 m/s2 * rE2
/ r), for r = 1.2, 1.4, 1.6, ..., 2.4 Earth radii, are usually within 1% of the velocities
required for circular orbits at these radii when using the simulation GRVFIELD.
- You should verify these results (be careful to use values of rE and r whose units are
compatible with those of the formula we have derived).
The figure below reviews the idea that the potential energy change between
surface of the earth and distance r from the surface is m * 9.8 m/s2 * rE2
(1 / rE - 1/r); Phy 241 students should understand this derivation thoroughly,
while other students should understand that the result is merely a symbolic way of
accurately calculating the work done to lift mass m from rE to r.
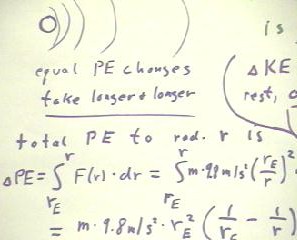
As r gets larger and larger, the force required to move away from earth at constant
velocity gets smaller and smaller, so the same change in potential energy requires greater
and greater changes in r.
- We can conclude from the preceding expression that the potential energy change from
distance r to effectively infinite distance is just m * 9.8 m/s2 * rE2
/ r.
It follows that if an object is 'dropped' from an effectively infinite distance to
distance r > rE from the center of the earth, and if it 'falls' without resistance, it
will attain a kinetic energy of m * 9.8 m/s2 * rE2 / r.
- Its velocity is therefore found by setting .5 m v2 equal to this expression,
as shown below.
- The resulting velocity v is v = `sqrt(19.6 m/s2 * rE2 / r).
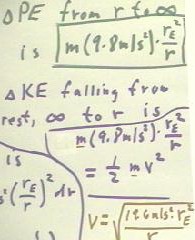
Video file #03
In particular, if r = rE, the required velocity is v = `sqrt(19.6 m/s2 * rE2
/ r) = `sqrt(19.6 m/s2 * rE2 / rE) = . . . = 11600 m/s
(approximately), as shown below.
- In fact, the ratio of this velocity to the velocity v = `sqrt(9.8 m/s2 * rE2
/ rE) of extreme low-earth orbit (the idealized velocity if it was possible to orbit at
the surface of the earth) is easily shown to be `sqrt(2).
- So the kinetic energy required for an object to completely escape the
gravitational field of the earth is just `sqrt(2) times that required for low-earth orbit.
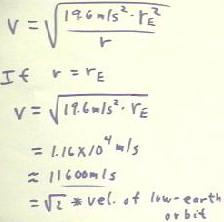
Video file #04
"
