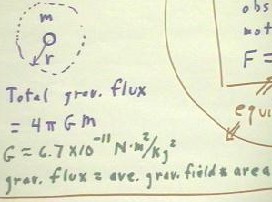"
Class Notes Physics I, 11/06/98
Newton's Law of Universal Gravitation; Orbital and Escape Velocities
Symbolic Expression of Universal Gravitation: The Flux Picture and
Newton's Formulation
We have investigated how the inverse-square nature of gravitation influences
gravitational field strength in the vicinity of Earth, orbital and escape velocities for
Earth, and kinetic and potential energy changes between circular orbits of different
orbital radii.
We will now generalize our picture in order to find expressions for the gravitational
field strength in the vicinity of any mass, and for the mutual attraction of any two
masses.
We will use two equivalent formulations.
- The first shows how the total gravitational flux, or total
gravitational influence of an object, is spread over larger and larger concentric spheres,
with the result that the gravitational field strength decreases according to the
inverse-square law we have already seen in the context of the gravitational field of
Earth.
The second relates the mutual attractive force between two masses to
the masses and the distance between their centers of mass.
The second is Newton's original formulation of the law of universal gravitation, which
was obtained as a mathematical model explaining the observed orbits of planets and the
Moon, while the first is a consequence of Newton's formulation.
The two pictures are equivalent, in that either can be derived from the other,
as we will see.
If we have a mass m, then we can think of that mass having a total gravitational flux
equal to 4 `pi G m, where G is the universal gravitational constant, equal to
approximately 6.7 * 10^-11 N m^2 / kg^2 (check the table in your text, inside the front
cover, to verify this unvalidated value).
- This flux is very much analogous to the flux of a light source.
- The flux of a light source can be expressed in watts of power.
For example, from a 100-watt point source of light, the energy produced at any instant
spreads out uniformly in all directions, so that the energy will at any instant be
uniformly distributed over a sphere centered at the source.
The radius of the sphere increases at the speed of light.
The entire 100 watts will therefore pass continuously through any such sphere which the
light has had time to reach.
However, for an increasingly large sphere the 100-watt flux of the light is spread out
over the increasingly large surface area of the sphere, and hence the light provides less
and less illumination.
We see that the illumination of the source is therefore inversely proportional to the
area, and hence to the square of the radius, of the sphere.
- More specifically, we define illumination as the number of watts per square meter
falling on the surface of a sphere
For a sphere of radius r, its area will be 4 `pi r^2 and the illumination at the surface
of the sphere will be 100 watts / 4 `pi r^2
This illumination will be measured in watts / m^2.
- For a gravitational mass, the total flux, 4 `pi G m, is analogous to the 100-watt flux
of the light source.
- It also spreads outward at the speed of light, and the resulting effect at any point is
equal to the flux per unit area.
Since the units of G * m are N m^2 / kg^2 * m = N m^2 / kg = (kg m / s^2) * m^2 / kg =
m^3 / s^2, the units of flux per unit area are (m^3 / s^2) / (m^2) = m / s^2.
These are the units of gravitational field strength, or gravitational
acceleration.
This gravitational acceleration is always directed toward the center of mass of the
planet (or of whatever the object with mass m might happen to be).
The figure below depicts a mass m and a sphere of radius r around the mass (the arrow
indicating the radius should extend from the center of the mass, not from its surface as
it appears in the figure below). The definition of gravitational flux is
- Gravitational flux through a surface = average gravitational field perpendicular to the
surface * area.
In the previous example of light flux, light is always traveling along straight lines
from the source, and is hence always perpendicular to the surface of the sphere.
- Gravitational influence can also
be thought of as traveling along straight lines from the source.
- If the source is spherically
symmetric, the symmetry of the situation ensures that these lines are radial from the
center of the source.
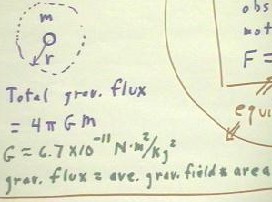
Newton's formulation states that if masses m1 and m2 are positioned so that their
centers of mass are separated by distance r, then there is a mutual gravitational force
between them, with the following characteristics:
- The force acts in the direction of the straight line between the centers of mass.
The magnitude of the force is F = G m1 m2 / r^2, as depicted below.
This formulation is completely equivalent to the flux formulation.

http://youtu.be/fLff-t3u0uM
We will use the flux formulation to find the force exerted by a 100 gram mass on a 70
gram mass, when the centers of mass are separated by 3 cm.
- The total flux of the 100 gram mass is found to be approximately 8.4 * 10 ^ -11 N m^2 /
kg, as shown below.
In the figure we note also that the area of the sphere centered at the 100 gram mass and
containing the 70 gram mass on its surface has radius 3 cm and therefore total surface
area .0113 m^2.
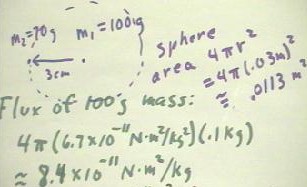
We find therefore that the gravitational field strength, equal to the total flux
divided by the area of the sphere, is 7.4 * 10^-9 m/s^2, so that the acceleration of the
70 gram mass toward the 100 gram mass is a = 7.4 * 10^-9 m / s^2.
- It follows from Newton's second
law that the force experienced by this mass is F = m a = 5.2 * 10^-10 Newtons.
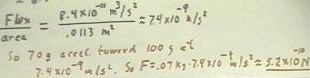
We could have calculated the force exerted on the 100 gram mass by the 70 gram mass in
a similar manner, using the acceleration corresponding to the flux of the 70 gram mass
spread out over a sphere of radius 3 cm to obtain this force.
- We would have obtained the same
result as above, as you should verify.
(We should note also that the
total momentum of the two masses, as they approach each other under the influence of their
mutual gravitational attraction, must be conserved.
- This follows from the fact that
equal and opposite forces are acting on the object.
- It follows that whenever the time
interval over which these forces act, the two forces will deliver equal and opposite
impulses, which will result in equal and opposite momentum changes.
- The total momentum of the system
will therefore remain unchanged.)
We can calculate the force F between the masses Newton's formulation F = G m1 m2 / r^2.
- Using this formulation we need not think of spheres and flux.
We think only of the line between the two centers of mass, and recall that the force
must be a force of attraction for both objects.
The calculation is straightforward. We merely substitute the masses m1 = .07 kg and m2
= .1 kg, and the separation r = .03 m of the centers of mass into the formula and we
obtain the same force as before, 5.2 * 10 ^ -10 Newtons.
- It is stated below that if the 100 gram mass is fixed, with a 70 gram mass free, the 70
gram mass will therefore accelerate at 7.4 * 10^-9 m/s^2, as obtained from Newton's second
law.
This is a true statement, but it is misleading.
Note carefully that in the figure below, it is not necessary for the 100 gram mass to
be fixed in order for the statement to be true.
- The statement is true whether or
not the 100 gram mass is fixed.
- If it is not fixed, then the
masses will approach their common center of mass and the distance between the masses will
change more quickly that if one of the masses is fixed.
- The attraction between the masses
and the resulting acceleration of the 70 gram mass at the instant when the masses are
three centimeters apart is the same in either case.
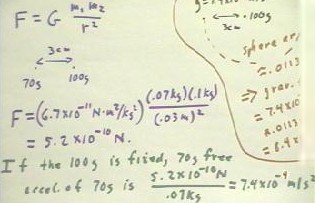
The preceding series of calculations showed us, among other things, that the
gravitational field strength at a distance of three centimeters from the 100 gram mass
must be 7.4 * 10 ^-9 m/s^2, since this is the acceleration experienced by an object at
this distance.
- This means that the gravitational flux through a sphere of radius three centimeters,
equal to the product of field strength and area, must be 8.4 * 10^-11 m^3 / s^2, as
indicated below.
- Thus we see that from Newton's formulation we obtain the same total gravitational flux
as from the flux formulation.
This should not be surprising, since the flux formulation came from Newton's
formulation.
note error in figure below:
7.4 * 10^-11 should read 7.4 * 10^-9 and 8.4 * 10^-9 should read 8.4 * 10^-11.

http://youtu.be/R5o-uqGXxAY
Deriving the flux picture from Newton's formulation
We now derive the flux formulation from Newton's formulation.
- We begin by considering to masses m1 and m2, with their centers of mass separated by
distance r.
We will calculate the total gravitational flux through this sphere and show that it is
indeed equal to 4 `pi G m.
Since by Newton's formulation, the force of attraction is F = G m1 m2 / r^2, the
acceleration of the mass m2 has magnitude
- g = F / m2 = [G m1 m2 / r^2] / m2 = G m1 / r^2.
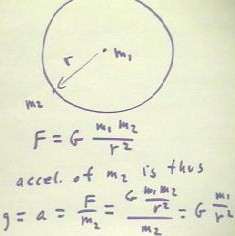
This gravitational acceleration is the gravitational field strength on the surface of
the sphere of radius r centered at the center of mass of mass m1.
- Since the area of this sphere is 4 `pi r^2, it follows that the total flux through the
sphere is
- total flux = gravitational field strength * area = G m1 / r^2 * 4 `pi r^2 = 4 `pi G m1.
This is the gravitational flux of m1, according to the flux picture. It has been
derived without using the flux picture, using only Newton's Law of Universal Gravitation.

http://youtu.be/DUu5BImvk_A
Orbital Velocity and Escape Velocity
We can now use either formulation we choose to obtain a formula for the velocity of a
small object in a circular orbit around a planet of mass M.
- At orbital radius r, a satellite of mass m will be at distance r from the center of the
planet and will therefore experience a gravitational acceleration g = F / m = [ G M m /
r^2] / m = G M / r^2.
Since this gravitational acceleration, as we have seen before, provides the centripetal
acceleration necessary to hold the satellite in a circular orbit, it must be equal to v^2
/ r.
We express the equality of these two expressions for the gravitational acceleration by

If we solve this equation for v, we obtain v = `sqrt(G M / r).
- This is the general relationship among planetary mass, orbital radius and orbital
velocity for any object whose mass is much less than M.
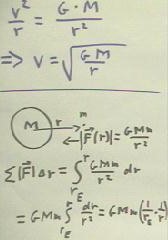
http://youtu.be/0c9mDDC9CFA
We can also obtain the expression for the work required to 'raise' an object
from the surface of Earth to distance r from the center.
- As before, we obtain the work by summing up the force * distance contributions
from small distance intervals over which force doesn't vary much.
- The force function is G M m / r^2, so we sum contributions of form F(r) `dr = G M
m / r^2 * `dr.
- In the limit as the intervals `dr approach zero we get the integral shown below,
integrated from the planetary radius rE to distance r from the center of the planet.
- The integral is straightforward for calculus students. Non-calculus
students can simply use the result, which is
- work required from Earth's surface to distance r from center = G M
m (1/rE - 1/r).
- This work is the potential energy change from the Earth's surface to distance r
from the center.
- It is consistent with the expression we derived before for this quantity.
We generalize this idea easily to an arbitrary planet with radius R.
- We find that the work done is now G M m (1/R - 1/r), where r is the distance from
planet center to which we 'raise' the mass m.
- As we increase the distance r, the quantity 1/r shrinks.
- As r continues to increase, 1/r shrinks to near zero.
- As r approaches infinity, 1/r approaches zero, and the work required approached G
M m / r.

It follows that if we have KE equal to G M m / R at the surface of the planet
(ignoring air resistance), we have the energy necessary to do the work required to 'raise'
an object of mass m to infinite distance.
- This quantity G M m / R is therefore called the 'escape energy'.
The associated velocity is the 'escape velocity'.
- If we let vEsc stand for escape velocity, we have KE = G M m / R, so 1/2 m vEsc^2
= G M m / r and we easily solve for v.
- We obtain escape velocity vEsc = `sqrt(2 G M / r).
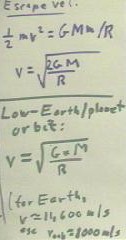
We note that for an orbit just above the surface of the planet, ignoring air
resistance, orbital velocity must be vOrb = `sqrt(G M / R).
- Comparing this with escape velocity, we see that vEsc = `sqrt(2) * vOrb.
- For example, for low-Earth orbit, orbital velocity is about 8000 m/s and escape
velocity is about 11,600 m/s (check these figures for yourself)
- The ratio vEsc / vOrb is `sqrt(2).
- This ratio applies to any spherically symmetric planet, ignoring atmospheric
resistance.
http://youtu.be/2rxyqsg1D0c
"